Счетчики со сквозным переносом
Для ускорения процесса счета необходимо, чтобы изменение состояний отдельных разрядов в счетчике происходило не последовательно, а непосредственно вслед за приходом очередного счетного сигнала (рис.2.7).
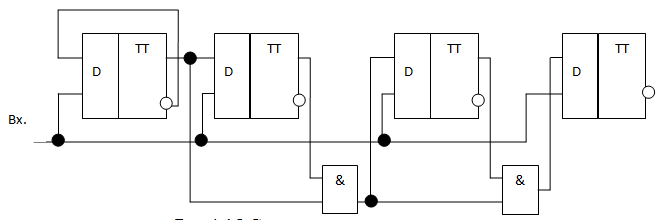
Рисунок 2.7– Счетчик со сквозным переносом
Синтез счетчиков с К≠2n.
Уменьшение числа устойчивых состояний в счетчике можно достигнуть
– за счет сброса счетчика в нулевое состояние по достижении некоторого кода в счетчике (рис.2.7);
– введения обратных связей (рис. 2.8).
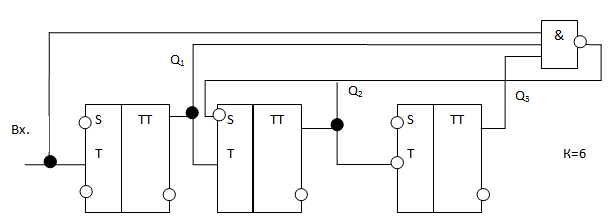
Рисунок 2.8 – Пересчетная схема с К=6
На рис.2.8 приведена пересчетная схема с К=6 и естественным порядком изменения состояний. Схема построена на Т-триггерах с последовательным переносом.
Пусть до прихода 1-го входного сигнала исходное состояние схемы 000, на выходе логической схемы И-НЕ U1. При поступлении 5 входных сигналов изменения состояний разрядов счетчика от 000 до 101 происходит в естественной последовательности двоичных чисел, т.к. на выходе схемы И-НЕ уровень логической единицы не изменяется. Под воздействием 6-го входного сигнала на выходе схемы И-НЕ формируется уровень логического 0, устанавливающий триггер 2 в состояние 1, т.е. состояние счетчика будет 111. Длительность входных сигналов должна быть достаточной, чтобы осуществитьустановку всех разрядов счетчика. При таком условии 6-й входной сигнал произведет переход счетчика в состояние 000, т.е. в исходное состояние.
Число n триггерных ячеек в пересчетной схеме с коэффициентом пересчета К должно удовлетворять условию 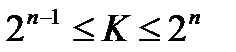 .
.
Пересчетные схемы с параллельным переносом строят на JK-триггерах со встроенными логическими элементами.
Произведем синтез пересчетной схемы с К=10 на JK триггерах. Из соотношения получим разрядность пересчетной схемы n=4, а число запрещенных состояний схемы M=2n-K = 16-10 = 6.
Пусть требуется построить счетчик с параллельным переносом и естественным порядком изменения состояний, закон функционирования которой задан табл.2.2:
Таблица 2.2
| Номер входного сигнала | 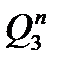 | 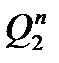 | 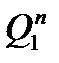 | 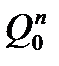 | 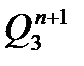 | 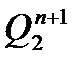 | 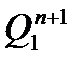 | 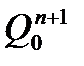 |
| 1. | ||||||||
| 2. | ||||||||
| 3. | ||||||||
| 4. | ||||||||
| 5. | ||||||||
| 6. | ||||||||
| 7. | ||||||||
| 8. | ||||||||
| 9. | ||||||||
| 10. |
Таблица 2.3 переходов JK-триггера
| Вид перехода JK-триггера | Логические уровни на входах | |
| J | K | |
| 0→0 | * | |
| 0→1 | * | |
| 1→0 | * | |
| 1→1 | * |
На основании таблиц 2.2 и 2.3 составим карты Карно для входов J и К всех триггеров пересчетной схемы. В картах Карно знак х означает запрещенные состояния схемы, для которых J и К для всех триггеров могут принимать произвольное значение (либо 0, либо 1); знак * означает произвольное значение J и К. Составим карты Карно-Вейча для минимизации функций возбуждения входов J и K всех триггеров
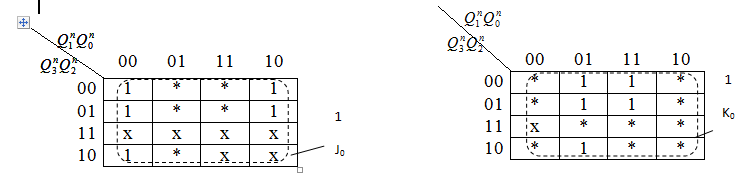
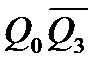 J1 J1 |
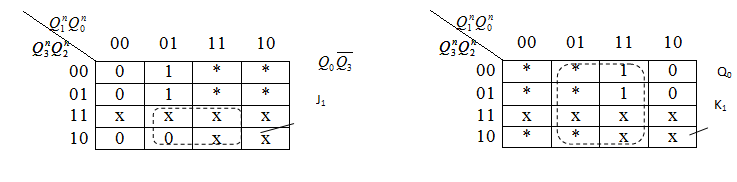
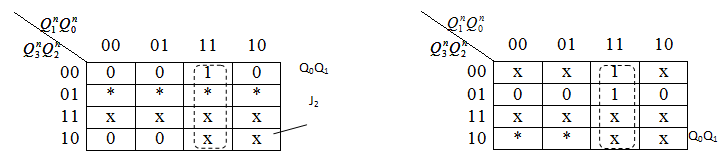
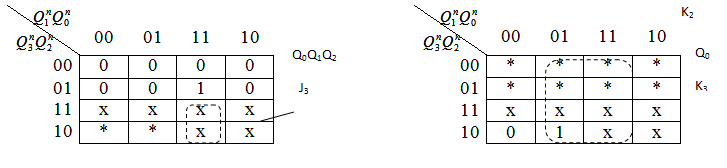
| Q0Q1 J2 |
После склеивания и минимизации с помощью карт Карно получим функции переключения (возбуждения) для J и К входов каждого триггера пересчетной схемы с параллельным переносом для К=10, то-есть
J0=1 J1= 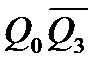 J2=Q0Q1 J3= Q0Q1Q2
J2=Q0Q1 J3= Q0Q1Q2
K0=1 K1=Q0 K2=Q0Q1 K3=Q0
Рисунок 2.9 – Схема счетчика с К=10
Рассмотрим работу схемы. Пусть показание счетчика 0111. Тогда на входе К триггеров Т1, Т2 и Т3 будут заблокированы по входу J уровнем логического 0 с выходов триггеров Т1, Т2 и Т3 соответственно. Показание счетчика будет 1001. Десятый входной сигнал вызовет переключение триггеров Т0 и Т3 , так как Т1 и Т2 будут заблокированы по входу J уровнем 0 с выходов соответствующих триггеров. Счетчик зафиксирует двоичный код 0000, то есть установится в исходное состояние.
Пересчетные схемы с К=10 называются декадными счетчиками.
Уменьшение числа устойчивых состояний в счетчике прямого счета путем введения обратных связей обеспечивает поступление дополнительных сигналов с какого-либо старшего разряда в младшие, обеспечивая при этом изменение естественной последовательности двоичных чисел при подсчете входных сигналов.
На триггерах, работающих в режиме Т и имеющих дополнительные входы R и S для синтеза пересчетных схем с последовательным переносом используют так называемый общий метод введения обратных связей.
Рассмотрим построение пересчетной схемы с обратными связями для К=12 на синхронных RS-триггерах с динамическим управлением, работающих в режиме Т. Разрядность схемы n=4, число запрещенных состояний
m=2n-K=16-12=410=01002.
Закон функционирования схемы задан таблицей переходов (табл.2.4):
Таблица 2.4
| Номер входного сигнала | Q3 | Q2 | Q1 | Q0 |
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| 6. | ||||
| 7. | ||||
| 8. | ||||
| OC | ||||
| 9. | ||||
| 10. | ||||
| 11. | ||||
| 12. |
Период следования входных сигналов схемы не может быть меньше 2t3cp, где t3cp – время задержки сигнала триггером. В противном случае восьмой входной сигнал будет воздействовать на триггер Т2 до прихода сигнала на его вход S по цепи обратной связи, что может привести к ошибке при подсчете входных сигналов. Частота выходных сигналов равна fвых=fвх/К.
Рисунок 2.10 – Вычитающий счетчик с К=12
Задание на самостоятельную работу
С использованием набора триггерных логических элементов выполнить схемы:
- реализации счетчика на JK-триггерах по модулю счета, заданному преподавателем,
-синхронного и асинхронного вычитателя на элементной базе, указанной преподавателем,
- управляемого суммирующего счетчика с параллельным переносом,
- синтезировать на D-триггерах схему асинхронного счетчика по модулю, заданному преподавателем.
