Блок «Поверхности 2-ого порядка»

Задача 1

Установить, что плоскость х-2=0 пересекает эллипсоид по эллипсу.

Найти его полуоси и вершины.

Ответ:3, 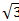; (2;3;0), (2;-3;0), (2;0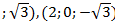

Задача 2

Установить, что плоскость z+1=0 пересекает однополостный гиперболоид 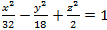по гиперболе.

Найти ее полуоси и вершины.

Ответ:4, 3; (4;0;-1), (-4;0;-1)

Задача 3

Установить, что плоскость y+6=0 пересекает гиперболический параболоид 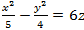по параболе.

Найти ее параметр и вершину.

Ответ:15; (0;-6;- )

Упрощение уравнений кривых и поверхностей 2-го порядка.

Задача 1

Привести уравнение к каноническому виду, определить тип уравнения, установить какой геометрический образ определяет уравнение. Изобразить на чертеже оси первоначальной системе координат, оси других координатных систем, которые вводятся по ходу решения и геометрический образ определяющий данным уравнением.

1)

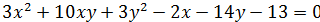
2)

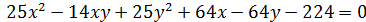
3)

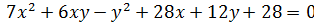
4)

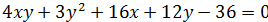
5)

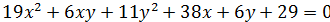
6)

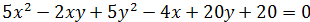
Задача 2

Определить какую поверхность задаёт следующие уравнения. Привести уравнение к каноническому виду и изобразить поверхность в прямоугольной декартовой системе координат.

1)

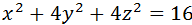
2)

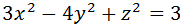
3)

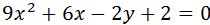
4)

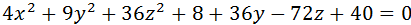
Квадратичные формы

Задача 1

Записать квадратичные формы в матричном виде, найти их ранг.

1)

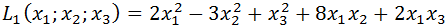
2)

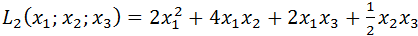
3)

Задача 2

Определить является ли квадратичная форма положительно определённой.

1)

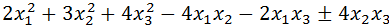
Задача 3

Найти все значения λ, при которых положительно определены следующие квадратичные формы.

1)

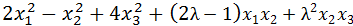
2)

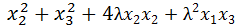
3)

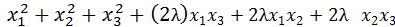
4)

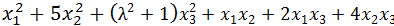
Задача 4

Привести квадратичные формы к диагональному виду, методом Лагранжа и записать соответствующее, не особенное линейное преобразование переменных.

1)

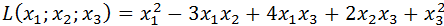
2)

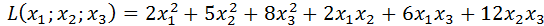
3)

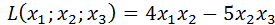
Линейная зависимость и независимость векторов. Базис.

Задача 1

Выяснить, является ли следующая система векторов заданной координатами в некотором базисе линейно зависимыми.

1)

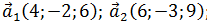
2)

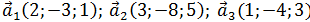
3)

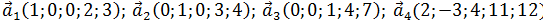
Задача 2

Найдите все значения 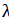, при которых вектор 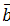линейно выражается через векторы .

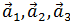1)

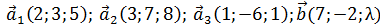
2)

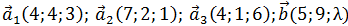
Задача 3

Найти координаты вектора 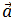(2;-1;7;10) в базисе:

1) (1;0;0;0) (0;1;0;0) (0;0;1;0) (0;0;0;1)

2) (0;0;1;0) (0;1;0;0) (0;0;0;1) (1;0;0;0)

Задача 4

Найти в базисе 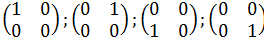координаты векторов пространства R(2x2)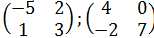

Задача 5

Показать, что система векторов представляет собой базис и найти координаты вектора 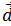в этом базисе.

1)

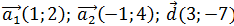
2)

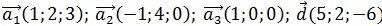
Задача 6

Дополнить до базиса пространство системы векторов заданных координатами в некотором базисе.

1)

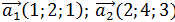
2)

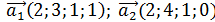
3)

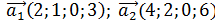
Задача 7

Дополнить до базиса соответствующего линейного пространства систему векторов.

1)

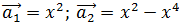
2)

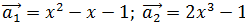
3)

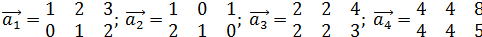
Задача 8

Найти матрицу перехода от базиса 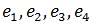к базису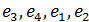

Задача 9

По координатам вектора Хв базисе 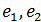найти его координаты в базисе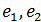

1)

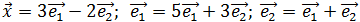
2)

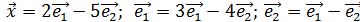
Задача 10

По координатам вектора Хв базисе 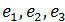, найти его координаты в базисе 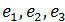, если

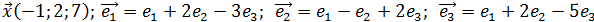
Евклидово пространство

Задача 1

Даны векторы евклидового пространства размерности n. Найти длины этих векторов (нормы), скалярное произведение векторов и угол между ними.

1)

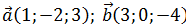
2)

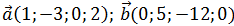
Задача 2

Являются ли ортогональными следующие системы векторов?

1)(0;1;1); (0;-1;3)

2)(1;0;0); (0;2;0); (0;0;3)

Задача 3

Даны векторы 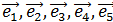образующие ортонормированный базис. Найти скалярное произведение x и y.

1)

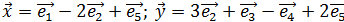
2)

3)

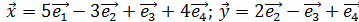
Линейный оператор и его матрица

Задача 1

Выясните, какие из указанных ниже отображений f: 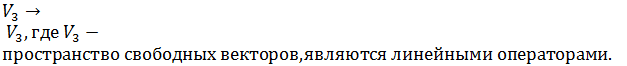Найдите матрицы линейных операторов в базисе i, j, k.Каждое преобразование описывается своим действием на произвольный вектор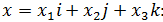

1)

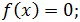
2)

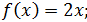
3)

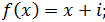
4)

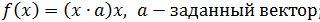
5)

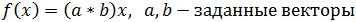
6)

7)

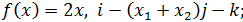
8)

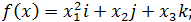
9)

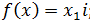
10)

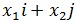
Укажите геометрический смысл преобразований 9) и 10)

Задача 2

Выясните, какие из преобразований 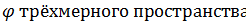являются линейными операторами, и найдите матрицы линейных операторов в том же базисе, в котором заданы координаты векторов

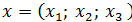и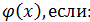

1)

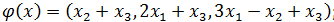
2)

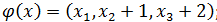
3)

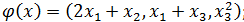
4)

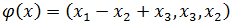
Задача 3

Выясните, существует ли линейный оператор двумерного пространства, переводящий вектор 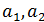соответственно в векторы 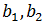и найдите матрицу этого оператора в базисе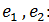

1)

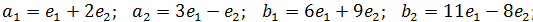
2)

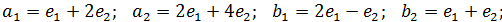
3)

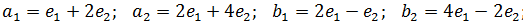
Задача 4

Выясните, существует ли линейны оператор трехмерного пространства, переводящий векторы 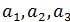соответственно в векторы 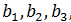и найдите матрицу этого оператора в том же базисе, в котором даны координаты всех векторов:

1)

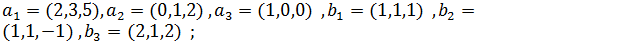
2)

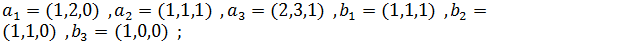
Задача 5

Линейный оператор f в базисе 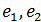имеет матрицу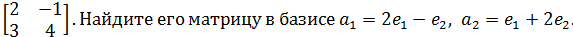

Задача 6

Линейный оператор f в базисе 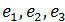имеет матрицу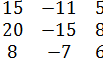

Найдите его матрицу в базисе 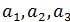, если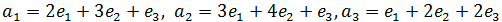

Задача 7

Линейны оператор f в базисе 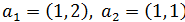имеет матрицу 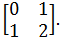Найдите его матрицу в базисе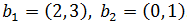

Задача 8

Линейны оператор f в базисе 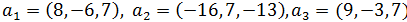имеет матрицу 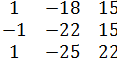. Найти его матрицу в базисе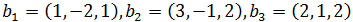

Задача 9

В базисе 1, 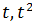пространства 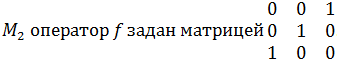Найдите матрицу этого оператора в базисе:

1)

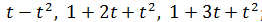
2)

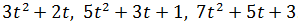
Задача 10

Линейны оператор f в базисе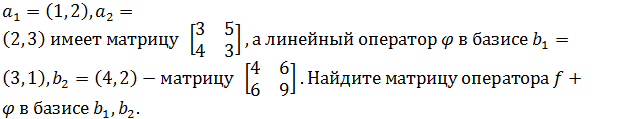

Задача 11

Линейны оператор f в базисе 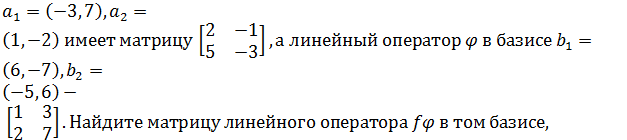в котором даны координаты всех векторов.