Деление отрезка в заданном отношении
Задача 1
Даны точки: А (3;-1) и В (2;1).
Определить:
1)Координаты точки М симметричной точке А, относительно точки В. 2)Координаты точки N симметричной точке В, относительно точки А.
Ответ:N=(4;-3) M=(1;3)
Задача 2
Даны три вершины параллелограмма А (3;-5), В (5;-3), С (-1;3).
Определить четвертую вершину D противоположную В.
Ответ:(-3;-5)
Задача 3
Даны вершины треугольника: А (1;4), В (3;-9), С (-5;2). Определить длину его медианы, проведённой из вершины В.
Ответ:13
Задача 4
Отрезок, ограниченный точками: А (1;-3) и В (4;2), разделён на 3 равные части. Определить координаты точек деления.
Ответ:(2;-1) и (3;1)
Задача 5
Даны вершины треугольника: А (3;-5), В (-3;3), С (-1;-2). Определить длину биссектрисы его внутреннего угла при вершине А.
Ответ: 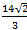
Полярная система координат
Задача 1
В полярной системе координат даны 2 вершины: А (3; 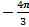 ) и В (5;
) и В (5; 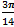 ) параллелограмма АВСD, точка пересечения диагоналей которого совпадает с полюсом. Определить две другие вершины этого параллелограмма.
) параллелограмма АВСD, точка пересечения диагоналей которого совпадает с полюсом. Определить две другие вершины этого параллелограмма.
Ответ:D (5; 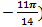 и С (1;
и С (1; 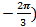
Задача 2
В полярной системе координат даны точки: А (8; 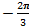 ) и В (6;
) и В (6;  ). Вычислить полярные координаты середины отрезка АВ.
). Вычислить полярные координаты середины отрезка АВ.
Ответ: С (1; 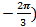
Задача 3
В полярной системе координат даны две противоположные вершины квадрата: Р (6; 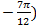 и Q (4;
и Q (4;  ). Определить площадь квадрата.
). Определить площадь квадрата.
Ответ: S=26+12 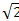
Задача 4
Полюс полярной системы координат совпадает с началом прямоугольной системой декартовых координат; а полярная ось совпадает с положительной полуосью абсцисс:
1) В полярной системе координат даны точки: 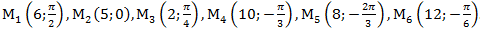
Определить, декартовы координаты этих точек.
2) В декартовой прямоугольной системе координат даны точки:
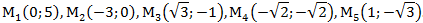
Определить полярные координаты этих точек.
Ответ:
1) 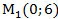
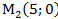
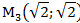
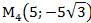
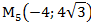
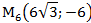
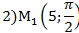
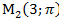
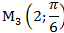
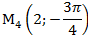
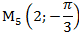
Задача 5
Установить какие линии определяются в полярных координатах следующими уравнениями:
1) 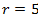 , 2)
, 2) 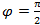 , 3)
, 3) 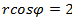 , 4)
, 4) 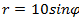
Ответ:
1) Окружность, 2) Луч, 3) Прямая,
4) Окружность R=5 с центром в точке (0;5).
Вектор. Координаты вектора.
Задача 1
Определить начало вектора  (2;-3;-1), если его конец совпадает с точкой
(2;-3;-1), если его конец совпадает с точкой
(1;-1;2)
Ответ: (-1;2;3)
Задача 2
Дан модуль вектора 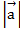 =2 и углы, которые вектор образует с координатными осями ОХ:
=2 и углы, которые вектор образует с координатными осями ОХ: 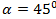 , ОУ:
, ОУ: 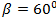 , OZ:
, OZ: 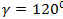 .
.
Вычислить проекции 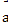 на координатные оси.
на координатные оси.
Ответ: ( 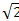 ;1;-1)
;1;-1)
Задача 3
Вычислить направляющие 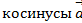 с координатами (12;-15;-16).
с координатами (12;-15;-16).
Ответ: ( 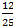 ;
; 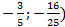
Задача 4
Может ли вектор составлять с координатными осями следующие углы:
1) 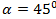 ,
, 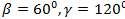
2) 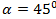 ,
, 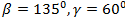
3) 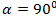 ,
, 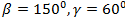
Ответ: Могут 1 и 3.
Задача 5
Вектор составляет с осями ОХ и OZ углы: 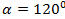 ,
, 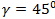 . Какой угол он составляет с осью ОУ?
. Какой угол он составляет с осью ОУ?
Ответ: 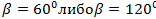
Задача 6
Вектор  составляет с координатными осями ОХ и ОУ углы:
составляет с координатными осями ОХ и ОУ углы:
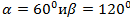 .
.
Вычислить его координаты при условии, что модуль вектора 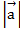 =2.
=2.
Ответ: (1;-1; 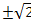 )
)
Линейные операции над векторами
Задача 1
Дано:
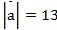
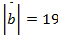
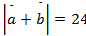
Найти: 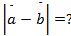
Ответ: 22
Задача 2
Дано:
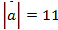
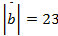
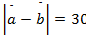
Найти: 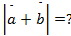
Ответ: 20
Задача 3
Даны 2 вектора  (3;-2;6) и
(3;-2;6) и 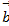 (-2;1;0).
(-2;1;0).
Определить проекцию на координатную оси и модули векторов 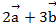 и
и 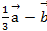
Ответ: 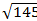 ;
; 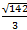
Задача 4
Проверить коллинеарность векторов  (2;-1;3) и
(2;-1;3) и 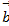 (-6;3;-9). Установить какой из них длиннее и во сколько раз.
(-6;3;-9). Установить какой из них длиннее и во сколько раз.
Как они направлены: в одну или противоположные стороны?
Ответ:
Вектор 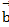 длиннее вектора
длиннее вектора  в 3 раза.
в 3 раза.
Задача 5
Определить при каких значениях 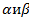 векторы:
векторы:
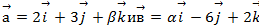 коллинеарны.
коллинеарны.
Ответ: 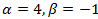
Задача 6
Проверить, что точки А (3;-1;2), В (1;2;-1), С (-1;1;-3), D (3;-5;3) служат вершинами трапеции.
Задача 7
Даны 3 вектора 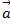 (3;-1),
(3;-1), 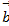 (1;-2),
(1;-2), 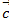 (-1; 7).
(-1; 7).
Определить разложение вектора 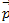 =
= 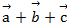 по базису
по базису 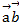 .
.
Ответ: p= 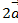 -3
-3 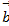
Задача 8
Даны 4 вектора  (2;1;0),
(2;1;0), 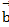 (1;-1;2),
(1;-1;2), 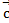 (2;2;-1),
(2;2;-1), 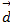 (3;7;-7).
(3;7;-7).
Определить разложения каждого из этих 4-х векторов принимая в качестве базиса 3 остальных.
Ответ:
· 2 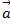 -3
-3 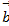 -
- 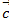
· -2 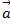 +3
+3 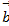 +
+ 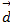
· 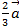 +
+ 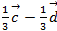
· 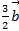 +
+