Физическая интерпретация формулы Даламбера

Для того, чтобы выяснить физический смысл решения (1.126), запишем функцию в виде суммы двух слагаемых

и ,

где ,

.

И выясним смысл и в отдельности.

Начнем с функции . Независимые переменные 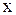и 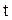изменяются так, что разность остается постоянной, т.е. . В таком случае и . Отсюда можно заключить следующее. Если точка 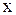движется с постоянной скоростью в положительном направлении оси , то смещение струны в этой точке во все время движения будет равно , оставаясь, таким образом, постоянным. Другими словами, значение смещения в точке в момент такое же, какое было в момент в точке . Построим графики этой функции для возрастающих значений 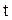: , , (рис. 1.4). Второй график ( ) будет сдвинут относительно первого ( ) на величину , третий ( ) – на величину и т.д. Если по очереди проектировать эти рисунки на неподвижный экран, то зритель увидит, что график, изображенный на верхнем рисунке, «побежит» вправо. (Этот способ изображения движения положен, между прочим, в основу съемки мультипликационных фильмов).

Смещение, распространяющееся в фиксированном направлении с некоторой скоростью, называется бегущей волной. Бегущую волну, распространяющуюся в направлении, выбранном за положительное, слева направо будем называть прямой волной.

Итак, прямая бегущая волна характеризуется решением .

Решению будет соответствовать движение смещения , аналогичное указанному, но совершаемое влево. Это движение называют обратной бегущей волной.

Если взять длинную натянутую веревку и слегка качнуть ее в середине, то по веревке влево и вправо побегут волны.

Постоянное число является скоростью распространения волн по струне.

Таким образом, решение (1.126) задачи Коши для бесконечной струны есть сумма (суперпозиция) двух волн , одна из которых распространяется направо со скоростью , а вторая – налево с той же скоростью. Это приводит к следующему графическому методу решения задачи о колебаниях бесконечной струны. Вычерчиваем кривые и , изображающие прямую и обратную волны в начальный момент времени , и затем, не изменяя их формы, передвигаем их одновременно со скоростью в разные стороны: - вправо, - влево. Чтобы получить график струны, достаточно построить алгебраические суммы ординат передвинутых кривых.

Формула (1.126) дает полное решение задачи. Исследуем эту формулу в одном простом случае, когда отсутствуют начальные скорости, т.е. когда . Из формулы (1.126) получаем

.

(1.127)

Так как функция 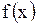известна, то мы можем вычислить для любых 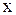и .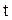

Пусть, например, струна в начальный момент времени имеет форму равнобедренного треугольника на интервале , вне этого интервала , а (рис. 1.5). Эти условия означают, что струна оттянута на участке и в момент без толчка отпущена. Покажем последовательные положения струны через промежутки времени . Согласно сказанному, колебания складываются из двух волн: прямой и обратной . Сначала вычертим графики прямой и обратной волны, а затем проследим за геометрией профиля струны через указанные
промежутки времени. В начальный момент профили прямой и обратной волны совпадают (рис. 1.6), что следует из формулы (1.127): , где .

Передвинем теперь графики и вправо и влево на расстояние . Тогда в результате сложения ординат этих графиков будем иметь форму струны в момент времени (рис. 1.7)

Передвинем графики и еще раз на расстояние , в результате будем иметь форму струны в момент времени (рис. 1.8).

При дальнейшем перемещении графиков и струна будет иметь форму, показанную на рис. 1.9, причем смещение струны вдвое меньше, чем соответствующее смещение на участке .

До тех пор, пока , имеется участок струны, где волны накладываются друг на друга, начиная с , волны начинают расходиться. В каждой точке струны после прохождения обеих волн (а для точек, лежащих вне области начального возмущения, после прохождения только одной волны) наступает покой. Такой процесс может наблюдаться в очень длинной струне до тех пор, пока волны, бегущие по струне, не дойдут до ее концов.