Влияние параметров на качество
АВТОМАТИЧЕСКИХ СИСТЕМ
Цель работы– изучение влияния изменения параметров системы на показатели качества и на характер протекающих в системе процессов.
Основные сведения
Важнейшими показателями качества (ПК) переходной характеристики (ПХ) 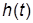 , или прямыми показателями качества системы являются:
, или прямыми показателями качества системы являются:
· время регулирования 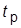 – время, по истечении которого ПХ не выходит из области допустимых (обычно пятипроцентных) отклонений от установившегося значения (УЗ)
– время, по истечении которого ПХ не выходит из области допустимых (обычно пятипроцентных) отклонений от установившегося значения (УЗ) 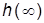 :
: 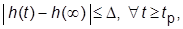 где
где 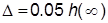 ;
;
· время нарастания 
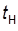 – время первого достижения УЗ;
– время первого достижения УЗ;
· перерегулирование 
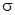 – превышение максимума ПХ над УЗ в процентах от УЗ:
– превышение максимума ПХ над УЗ в процентах от УЗ: 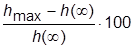 .
.
Среди косвенных ПК систем автоматического управления широко употребляются частотные и корневые.
Некоторые частотные ПК:
· частота среза 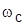 – частота, при которой ЛАХ разомкнутой системы пересекает ось абсцисс:
– частота, при которой ЛАХ разомкнутой системы пересекает ось абсцисс: 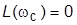 ; служит мерой быстродействия системы;
; служит мерой быстродействия системы;
· запас устойчивости по фазе 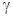 – превышение ЛФХ разомкнутой системы на частоте среза над уровнем –
– превышение ЛФХ разомкнутой системы на частоте среза над уровнем – 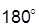 (в устойчивой системе):
(в устойчивой системе): 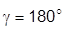 + +
+ + 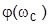 ; с уменьшением
; с уменьшением 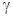 переходные процессы становятся более колебательными;
переходные процессы становятся более колебательными;
· полоса пропускания 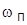 – частота, при которой значение АЧХ замкнутой системы в
– частота, при которой значение АЧХ замкнутой системы в 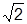 раз меньше ее значения на нулевой частоте:
раз меньше ее значения на нулевой частоте: 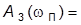
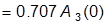 или
или 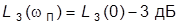 ; является мерой быстродействия системы;
; является мерой быстродействия системы;
· показатель колебательности 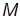 – отношение максимального значения АЧХ замкнутой системы к начальному значению:
– отношение максимального значения АЧХ замкнутой системы к начальному значению: 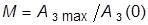 ; характеризует склонность системы к колебаниям.
; характеризует склонность системы к колебаниям.
Основные корневые ПК:
· степень устойчивости 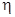 – расстояние от мнимой оси до ближайшего корня (или пары комплексно-сопряженных корней) характеристического полинома (ХП) замкнутой системы; является мерой быстродействия; если ПФ не имеет нулей, то при увеличении действительной и мнимой частей каждого полюса в
– расстояние от мнимой оси до ближайшего корня (или пары комплексно-сопряженных корней) характеристического полинома (ХП) замкнутой системы; является мерой быстродействия; если ПФ не имеет нулей, то при увеличении действительной и мнимой частей каждого полюса в  раз длительность переходного процесса сократится также в
раз длительность переходного процесса сократится также в  раз;
раз;
· колебательность 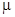 – отношение модулей мнимой и вещественной частей ближайшей к мнимой оси пары комплексных корней ХП; чем больше
– отношение модулей мнимой и вещественной частей ближайшей к мнимой оси пары комплексных корней ХП; чем больше 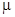 , тем меньше затухание колебаний за период.
, тем меньше затухание колебаний за период.
Некоторые способы суждения об устойчивости системы:
· для асимптотической устойчивости необходимо и достаточно, чтобы все корни ХП располагались в левой полуплоскости; если один корень находится в начале координат или одна пара корней – на мнимой оси (остальные – в левой полуплоскости), то система находится на границе устойчивости – соответственно, апериодического или колебательного типа);
· в асимптотически устойчивой системе все коэффициенты ХП положительны; если хотя бы один из коэффициентов ХП отрицателен, система неустойчива;
· согласно критерию Гурвица, для асимптотической устойчивости системы третьего порядка с положительными коэффициентами ХП необходимо и достаточно, чтобы произведение двух средних коэффициентов было больше произведения двух крайних коэффициентов (для колебательной границы устойчивости имеет место равенство этих произведений);
· согласно критерию Найквиста, если ПФ разомкнутой системы имеет полюсы только в левой полуплоскости (кроме, возможно, одного нулевого), то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении частоты от нуля до бесконечности АФХ разомкнутой системы не охватывала точку с координатами (–1, j0), или, что то же самое, чтобы разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФХ через луч ( 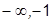 ] равнялась нулю; в терминах ЛЧХ это соответствует тому, что в диапазоне частот, где ЛАХ разомкнутой системы лежит выше оси, разность между числом положительных (снизу вверх) и отрицательных (сверху вниз) переходов ЛФХ через горизонтальную прямую с ординатой
] равнялась нулю; в терминах ЛЧХ это соответствует тому, что в диапазоне частот, где ЛАХ разомкнутой системы лежит выше оси, разность между числом положительных (снизу вверх) и отрицательных (сверху вниз) переходов ЛФХ через горизонтальную прямую с ординатой 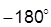 равняется нулю.
равняется нулю.
Программа работы
Работа рассчитана на два занятия: программа первого включает задания 2.2.1 и 2.2.2, второго – 2.2.3.
2.2.1. Исследование влияния контурного коэффициента
усиления системы на ее динамические свойства
1. Задать структурную схему системы третьего порядка, составленную из последовательно соединенных звеньев с ПФ 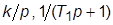 и
и 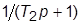 , охваченных единичной отрицательной обратной связью. Назначить
, охваченных единичной отрицательной обратной связью. Назначить 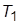 в соответствии с нижеприведенными вариантами и задать
в соответствии с нижеприведенными вариантами и задать 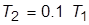 :
:
| Вариант | ||||||||||
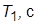 | 1.0 | 0.1 | 2.0 | 0.2 | 2.5 | 0.25 | 0.8 | 0.5 | 0.4 | 4.0 |
2. Для значений  , равных
, равных 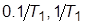 и
и 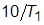 , определить и занести в таблицу значения
, определить и занести в таблицу значения 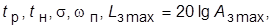 корней ХП,
корней ХП, 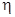 и
и 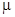 . Описать изменение характера переходного процесса с увеличением
. Описать изменение характера переходного процесса с увеличением  .
.
3. Увеличить  до значения
до значения 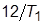 . Ответить на вопросы: каким стал переходный процесс? какие изменения произошли с корнями ХП?
. Ответить на вопросы: каким стал переходный процесс? какие изменения произошли с корнями ХП?
4. Разомкнуть обратную связь. Для значений  , указанных в пп. 2 и 3, определить и занести в таблицу
, указанных в пп. 2 и 3, определить и занести в таблицу 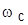 и (только для первых трех значений
и (только для первых трех значений  )
) 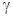 , а также исследовать с позиций критерия Найквиста изменения, происходящие в АФХ и ЛЧХ с ростом
, а также исследовать с позиций критерия Найквиста изменения, происходящие в АФХ и ЛЧХ с ростом  .
.
2.2.2. Исследование влияния относительной инерционности
звеньев системы на ее устойчивость
5. В предыдущей схеме, но с замкнутой обратной связью и со значением  , назначенном в п. 3, уменьшить
, назначенном в п. 3, уменьшить 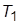 в 4 раза. Описать изменения, произошедшие в характере переходного процесса и в расположении корней ХП.
в 4 раза. Описать изменения, произошедшие в характере переходного процесса и в расположении корней ХП.
6. Задать структурную схему системы, состоящей из трех последовательно соединенных апериодических звеньев с постоянными времени 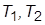 и
и 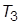 , охваченных единичной отрицательной обратной связью. Одно из звеньев имеет коэффициент передачи
, охваченных единичной отрицательной обратной связью. Одно из звеньев имеет коэффициент передачи  , остальные – единичный.
, остальные – единичный.
7. Назначить 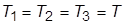 , где
, где 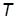 – произвольная константа. Подобрать такое значение
– произвольная константа. Подобрать такое значение 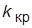 контурного коэффициента
контурного коэффициента  , при котором система выйдет на колебательную границу устойчивости, т. е. ПХ примет вид незатухающих колебаний. Определить частоту
, при котором система выйдет на колебательную границу устойчивости, т. е. ПХ примет вид незатухающих колебаний. Определить частоту 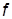 , Гц, этих колебаний.
, Гц, этих колебаний.
8. Назначить 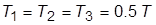 . Снова определить
. Снова определить 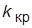 и
и 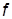 , сравнить их с предыдущими значениями.
, сравнить их с предыдущими значениями.
9. Оставив 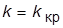 , задать новое соотношение постоянных времени:
, задать новое соотношение постоянных времени: 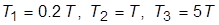 . Охарактеризовать изменения, произошедшие в свойствах системы. Увеличением
. Охарактеризовать изменения, произошедшие в свойствах системы. Увеличением  определить новое значение
определить новое значение 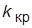 .
.
10. По результатам исследований в пп. 5–9 ответить на вопрос: какие факторы – абсолютные значения постоянных времени или их соотношения – влияют на устойчивость, характер переходных процессов в системе и на ее критический коэффициент усиления ?
2.2.3. Изучение стандартных полиномов
и диаграммы Вышнеградского
11. Задать структурную схему системы третьего порядка в управляемой канонической форме (рисунок).
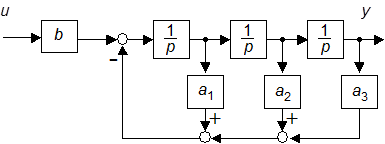
12. Задать систему с единичным коэффициентом передачи и ХП Баттерворта, для чего назначить 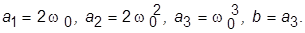 Значение
Значение 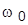 взять из приведенных ниже:
взять из приведенных ниже:
| Вариант | ||||||||||
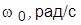 | 2,5 |
13. Определить корни ХП и установить закономерность их геометрического расположения на комплексной плоскости. Определить 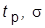 и
и 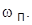
14. Повторить анализ, увеличив 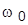 в 2 раза.
в 2 раза.
15. Задать систему с биномиальным ХП, назначив 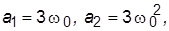
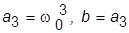 (оставить первоначальное значение
(оставить первоначальное значение 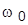 ) и повторить п. 13.
) и повторить п. 13.
16. Задать звено с ПФ 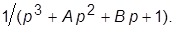
| Параметр | Номер опыта | |||||
| A | 0.5 | |||||
| B | 0.5 |
17. Последовательно задавать комбинации значений параметров Вышнеградского 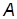 и
и 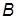 согласно таблице. Для каждого из сочетаний определить полюсы ПФ и описать характер ПХ.
согласно таблице. Для каждого из сочетаний определить полюсы ПФ и описать характер ПХ.
Содержание отчета
1. Структурные схемы и численные значения их параметров.
2. Результаты по каждому пункту программы работы и комментарии к ним. Ответы на вопросы, содержащиеся в программе работы.
3. Вычисление критических значений контурного коэффициента в заданиях 2.2.1 и 2.2.2 исходя из условия нахождения системы на границе устойчивости (по критерию Гурвица). 
4. Графики зависимости 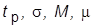 и
и 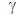 от
от  . При определении
. При определении 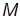 учесть, что
учесть, что 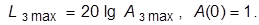 (Прокомментировать графики, изобразив по ПФ (см. начало программы работы) асимптотические ЛАХ разомкнутой системы при различных
(Прокомментировать графики, изобразив по ПФ (см. начало программы работы) асимптотические ЛАХ разомкнутой системы при различных 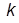 и (эскизно) ЛФХ.)
и (эскизно) ЛФХ.)
5. Значения корней стандартных полиномов и значения 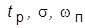 с анализом влияния на них значения
с анализом влияния на них значения 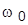 и пояснением связи характера ПХ с картиной расположения корней на плоскости.
и пояснением связи характера ПХ с картиной расположения корней на плоскости.
6. Эскиз диаграммы Вышнеградского с нанесенными на нее точками, определяющими заданные в таблице на с. 11 сочетания параметров 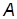 и
и 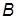 ; вывод о связи характера ПХ с полюсами ПФ.
; вывод о связи характера ПХ с полюсами ПФ.
Для построения диаграммы необходимо:
· изобразить систему координатных осей для параметров 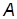 (ось абсцисс) и
(ось абсцисс) и 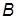 (ось ординат); оцифровку осей задать в пределах от 0 до 6;
(ось ординат); оцифровку осей задать в пределах от 0 до 6;
· изобразить границу устойчивости согласно уравнению 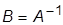 (выше этой границы располагается область устойчивости);
(выше этой границы располагается область устойчивости);
· для значений 0 < A £ 3 изобразить кривую DC, описываемую уравнением 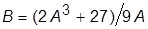 ; правая граница этой кривой – точка C имеет координаты (3;3);
; правая граница этой кривой – точка C имеет координаты (3;3);
· изобразить кривые CE и CF (симметричные относительно биссектрисы квадранта), которые описываются одним и тем же параметрически заданным уравнением 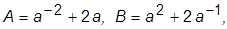 где
где 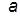 – параметр; для построения кривой CE необходимо задавать
– параметр; для построения кривой CE необходимо задавать 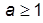 (здесь
(здесь 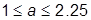 ), а для построения кривой CF – 0 < a £ 1 (здесь
), а для построения кривой CF – 0 < a £ 1 (здесь 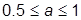 );
);
· обозначить цифрами I, II, и III следующие области:
I – между границей устойчивости и линией DCF (в этой области ХП имеет один вещественный корень и пару комплексно-сопряженных корней, расположенных ближе к мнимой оси, чем вещественный);
II – выше кривой DCE (здесь ХП имеет те же типы корней, что и в области I, но ближайшим к мнимой оси является вещественный корень);
III – между кривыми CF и CE (здесь все корни ХП вещественны).
2.4. Контрольные вопросы
1. Дайте определения основных показателей качества динамики САУ.
2. Как уменьшение запаса устойчивости отражается на значениях других показателей качества ?
3. Какими мерами можно повысить критическое значение контурного коэффициента усиления системы?
4. В чем польза диаграммы Вышнеградского?
5. Почему граница устойчивости на диаграмме описывается уравнением 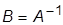 ?
?
6. Каковы значения корней ХП в точке C ?
Лабораторная работа № 3
