Модели неуправляемых и управляемых выпрямителей

Работа приведенного на рис.3.10 управляемого выпрямителя сводится к циклической смене двух типов состояний схемы:

1). Состояние проводимости, когда открыты два тиристора (тиристор VS_A(a) анодной (а) группы фазы А и тиристор VS_В(к) катодной (к) группы фазы В) и нагрузка находится под линейным напряжением е_АВ (рис.3.11,а);

2). Состояние коммутации, когда открыты три тиристора (тиристор VS_A(a) анодной (а) группы фазы А, тиристор VS_В(к) катодной (к) группы фазы В и тиристор VS_С(к) катодной (к) группы фазы С) и происходит коммутация токов в двух тиристорах (рис.3.11,б) – вводимом в работу VS_С(к) и выводимом VS_В(к).

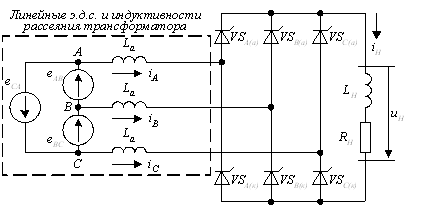
Рисунок 3.10 - Схема управляемого выпрямителя

На рис.3.11 открытые тиристоры изображены перемычками отмечены ток нагрузки i_H, ток коммутации i_К во вводимом в работу тиристоре VS_С(к) и ток коммутации i_δ в выводимом из работы тиристоре VS_В(к).

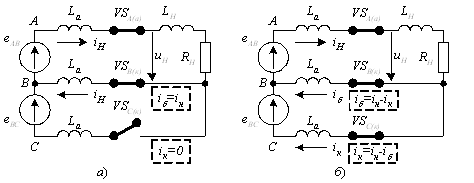
Рисунок 3.11 - Состояния схемы трехфазного мостового управляемого выпрямителя

Схема коммутации (рис.3.11,б) описывается системой уравнений:

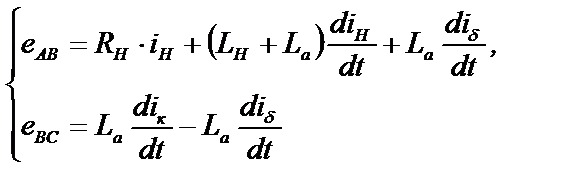
или

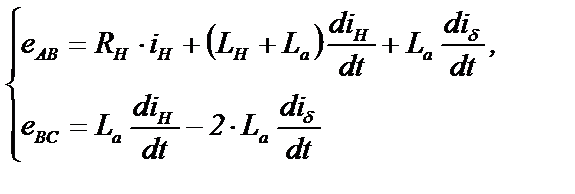(3.21)

Схема в состоянии проводимости (рис.3.11,а) описывается системой уравнений

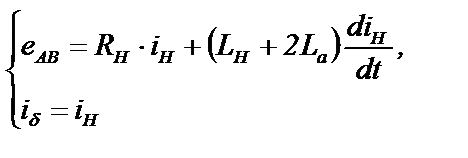(3.22)

Объединение выражений (3.21) и (3.22) для двух состояний схемы дает

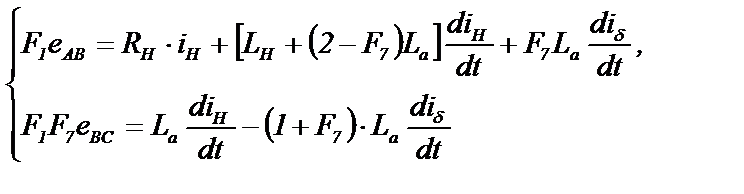(3.23)

где F₁ и F₇ - функции состояния схемы (ключи), принимающих значения 0 или 1, причем функцией F₁ определяется интервал проводимости (при F₁=1), а функцией F₇ - интервал коммутации (при F₇=1).

Обобщением выражения (3.23) на все возможные состояния схемы на рис.3.10 является

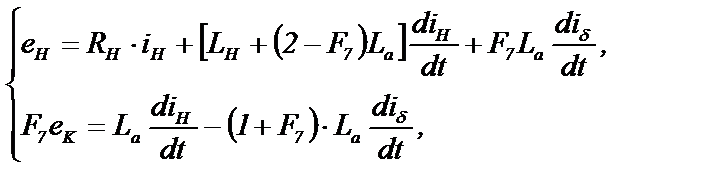(3.24)

где e_H=(F₁-F₄)e_AB+(F₃-F₆)e_BC+(F₅-F₂)e_CA – обобщенная э.д.с., приложенная к нагрузке;

e_K=(F₁-F₄)e_BC+(F₃-F₆)e_CА+(F₅-F₂)e_AB – обобщенная э.д.с., действующая в цепи коммутации.

При моделировании удобно вместо аргумента – времени t использовать переменную фазы θ, которая связана с временем зависимостью θ=ωt. Тогда в системе (3.24) индуктивность L будет заменена на индуктивное сопротивление X в соответствии с соотношением X=ωt. Система (3.24) примет вид

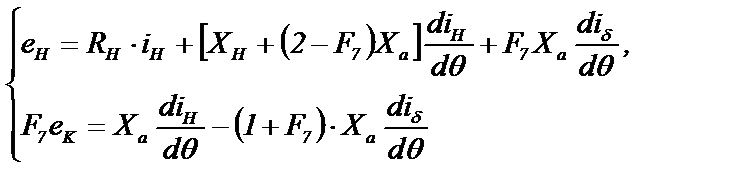(3.25)

Графики функций состояния F₁…F₇ приведены на рис.3.12. Функциями F₁…F₆ задаются интервалы проводимости схемы в разных ее состояниях, а функцией F₇ задаются интервалы коммутации.

На рис.3.12 обозначено: α - угол управления выпрямителя, λ - угол проводимости в течение такта работы схемы, γ - угол коммутации тиристоров. Окончание коммутации тиристров определяется моментом времени, когда ток i_δ обращается в ноль. На интервалах коммутации ненулевой является только функция F предыдущего интервала проводимости.

Модель неуправляемого выпрямителя является частным случаем управляемого, когда угол управления α равен 0.

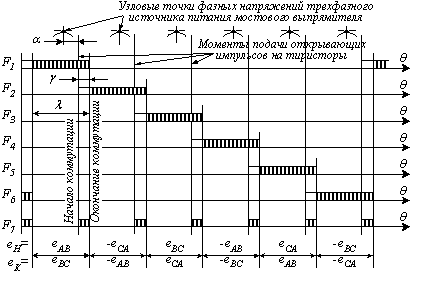
Рисунок 3.12 - Функции состояния схемы, значения е_н и е_к на интервалах проводимости и значения углов α, γ и λ

Вопросы для самоконтроля

1. Какие существуют состояния схемы управляемого выпрямителя?

2. Приведите систему уравнений для состояния коммутации схемы управляемого выпрямителя.

3. Приведите систему уравнений для состояния проводимости схемы управляемого выпрямителя.

4. Как определяется значение обобщенной э.д.с., приложенной к нагрузке?

5. Как определяется значение обобщенной э.д.с., приложенной к цепи коммутации?

6. Поясните процедуру замены в модели аргумента времени t на аргумент углаθ .

7. Поясните графики, приведенные на рис.3.12.

Литература [1-9]

3.8 Методика моделирования устройств преобразовательной техники

Работа устройств преобразовательной техники сводится к циклической смене конечного числа состояний схемы. Так как отдельные состояния схемы подобны друг другу, то возможно обобщенное описание схемы одной системой уравнений, в которую вводятся переменные-функции состояния (ключи). Тогда перебор всех состояний схемы сводится к перебору значений функций состояния, а не схем и систем уравнений, что, конечно, существенно упрощает моделирование.

Значения функций состояния зависит от номера такта в течение периода повторяемости схемы. Целесообразно ввести функцию номера такта, по значению которой согласно вышеприведенных графиков функций состояния можно определять значения этих функций. На рис.3.13 приведена такая программа и результат ее выполнения. В программе использована функция floor(X) определения целой части числа Х. В приведенной программе вычисления ведутся по переменной t, которые легко могут быть преобразованы в вычисления по переменной θ.

Рисунок 3.13 - Программа вычисления функции n(t) номера такта в периоде

повторяемости состояний преобразовательного устройства

Далее решается обобщенная система уравнений с определением в процессе счета значений функций состояния. Методы расчета функций состояния в зависимости от t или от θ для различных типов преобразовательных устройств имеют как много общего, так и имеют особенности, обусловленные спецификой схем и алгоритмов их работы.

Моделирование автономного инвертора напряжения (рис.3.7)

Перепишем систему уравнений (3.19) в матричном виде

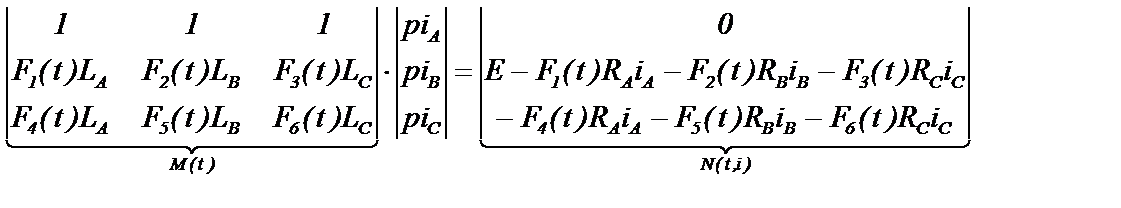(3.26)

Решением системы (3.29) относительно переменных pi_A, pi_B, pi_C является матрица S(t,i) размером 3х1, которая определяется в пакете MathCAD с помощью стандартной функции lsolve решения системы линейных уравнений:

S(t,i):=lsolve(M(t),N(t,i)) (3.27)

Решение S(t,i) имеет нормальную форму Коши и, поэтому оно может использоваться в стандартной функции Rkadapt решения системы дифференциальных уравнений:

z:=Rkadapt(i_НАЧ, t_НАЧ , t_КОН , N_ВЫВ , S(t,i)), (3.28)

где i_НАЧ - вектор начальных условий для токов i_А, i_В и i_С.

Значения функций состояния могут быть определены в соответствии с табл.3.1 и рис.3.13 выражениями

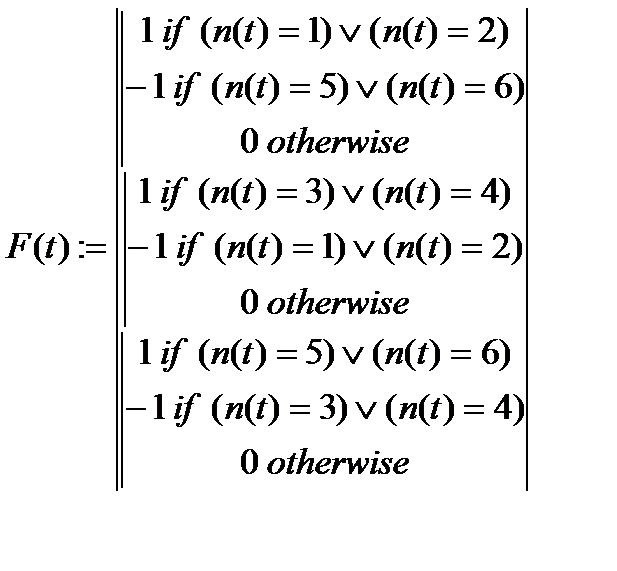
(3.29)

Из этих выражений значения функций переключения определятся как

F₁(t)=F(t)₀, F₂(t)=F(t)₁, F₃(t)=F(t)₂,

F₄(t)=F'(t)₀, F₅(t)=F'(t)₁, F₆(t)=F'(t)₂ (3.30)

Если учесть вытекающие из табл.3.1 равенства

F₁(t)+F₂(t)+F₃(t)=0, F₄(t)+F₅(t)+F₆(t)=0 (3.31)

то выражения (3.29) могут быть упрощены - вместо расчета матриц из трех строчек достаточно рассчитать матрицы из двух строчек, например F₁(t), F₂(t) и F₄(t), F₅(t).

Моделирование управляемого выпрямителя (рис.3.10)

Выход на функцию решения дифференциальных уравнений вида (3.28) такой же как и при моделировании АИН.

Аргументом всех функциональных зависимостей является переменная θ с произвольным диапазоном изменения. Из нее образуется переменная φ(θ) с диапазоном изменения равным 2π:

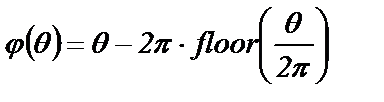(3.32)

Линейные напряжения будут вычисляться по формулам

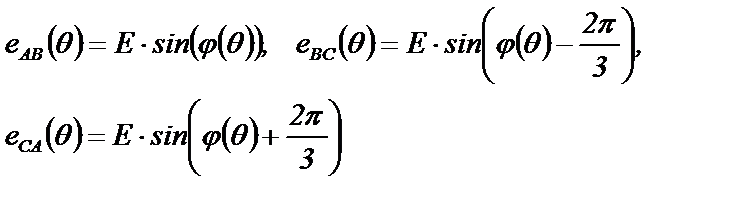(3.33)

Так как графики функций состояния для выпрямителя (рис.3.12) существенно отличаются от графиков для АИН (рис.3.8), то и способ их определения для выпрямителя будет существенно иным, чем для АИН, задаваемым выражениями (3.29), (3.30) и (3.31).

Выполняются следующие вычисления:

1). Задается строчная матрица F0:=|0 0 0 0 0 0 0|, которая транспонированием F:=F0^T превращается в столбцовую матрицу F.

2). Вычисляется индекс n1(θ) активного линейного напряжения в фазе коммутации тиристоров

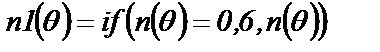(3.34)

3). Определяется момент формирования открывающего импульса на тиристор и одновременно начало процесса коммутации тиристоров

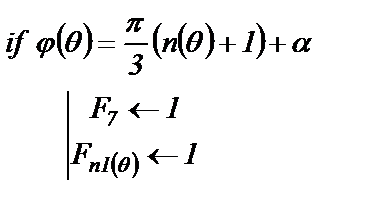(3.35)

Для того, чтобы было выполнено равенство 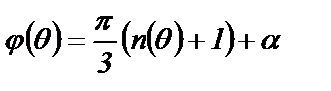, необходимо задавать значение α кратным шагу изменения угла θ.

4). Определяется момент завершения коммутации тиристоров и переход в состояние проводимости схемы

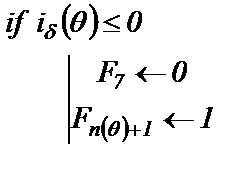(3.36)

Вопросы для самоконтроля

1. Как определяется помер n(t) такта состояния схемы в функции текущего времени t?

2. Как приводится система дифференциальных уравнений модели АИН к нормальной форме?

3. Составьте формулы для определения значений функции состояния F₁ , F₂ и F₃ модели АИН в зависимости от номера такта n(t).

4. Составьте формулы для определения значений функции состояния F₄ , F₅ и F₆ модели АИН в зависимости от номера такта n(t).

5. Приведите формулу преобразования угла θ, который изменяется в произвольном диапазоне к углу φ(θ) с диапазоном изменения от 0 до 2π.

6. Поясните алгоритм вычислений, применяемых при моделировании выпрямителей.

Литература [1-9]