Аналитический метод расчета токов короткого замыкания СГ.

Операторное сопротивление х_q(р) СГ по оси q

Вводная часть.

Выполним вывод выражения тока короткого замыкания (КЗ) в функции времени. Далее из полученного выражения определим величину ударного тока i_уд. Ударным током называют наибольший максимум мгновенного значения тока КЗ. Ударный ток используется для проверки автоматических выключателей на термическую стойкость. Для таких расчетов режим КЗ можно считать проходящим при следующих допущениях:

1). КЗ считается трехфазным металлическим непосредственно на выводах обмотки статора СГ. Поэтому

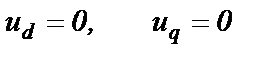(2.20)

Этот вид короткого замыкания является самым опасным для генератора, так как ударный ток достигает абсолютного максимума.

2). Перед моментом КЗ генератор работал вхолостую, поэтому значение угла нагрузки q СГ равно нулю. Такое допущение имеет то обоснование, что. как показывают расчеты, величина ударного тока КЗ практически не зависит от уровня загрузки СГ до момента КЗ.

3). Во время КЗ частота вращения СГ неизменна и поэтому

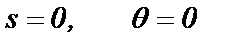(2.21)

4). Во время КЗ напряжение возбуждения остается постоянным

u_f=const (2.22)

Два последних допущения обосновываются тем, что ударный ток образуется спустя ≈10 мс от момента КЗ, и за такое время как скольжение s, так и угол нагрузки θ и напряжение возбуждения u_f практически не изменятся.

Система уравнений Парка-Горева для режима КЗ будет следующей:

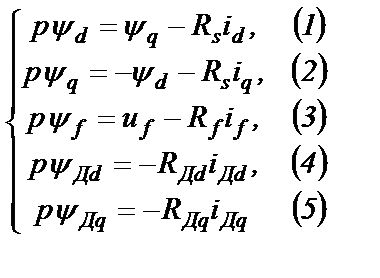(2.23)

Формулы для расчета потокосцеплений те же, что и (2.13).

Система уравнений (2.23) линейная и может быть решена аналитически.

Аналитический метод состоит из 4-х этапов:

1). Определение операторного сопротивления СГ по поперечной оси x_q(p).

2). Определение операторного сопротивления СГ по продольной оси x_d(p).

3). Определение изображения по Лапласу тока КЗ i_КЗ(р).

4). Определение оригинала тока КЗ i_КЗ(t).

Расчет операторного сопротивления x_q(p) СГ по поперечной оси.

Из уравнений (9) и (12) системы (2.13) и из уравнения (5) системы (2.23) образуем систему

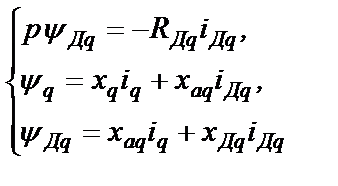(2.24)

Система (2.23) из 3-х уравнений содержит 4 переменные 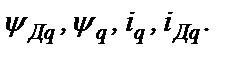Из него можно выразить любую из этих переменных через любую другую в виде линейной зависимости.

Выведем выражение вида

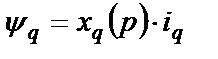(2.25)

Для этого сначала исключим из системы (2.24) переменную _Дq:

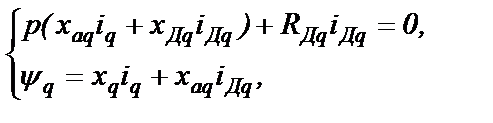(2.26)

а затем исключим переменную i_Дq:

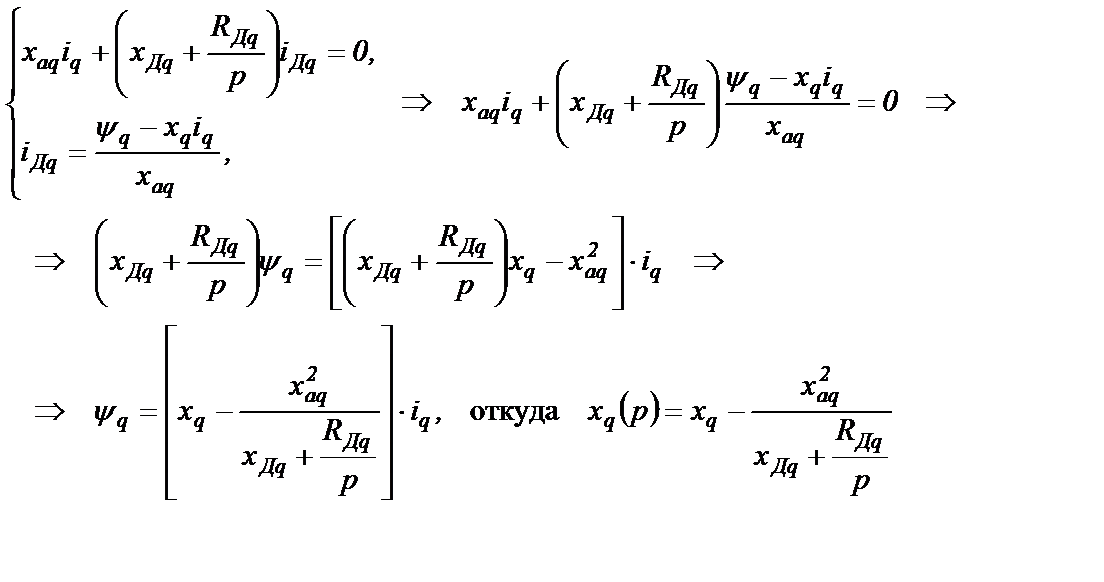(2.27)

Для дальнейших расчетов, в которых будет использоваться сопротивление x_q(p), представим его в двух формах записи: в форме сопротивлений и в форме постоянных времени.

а). Приведение x_q(p) к форме сопротивлений.

Преобразуем x_q(p), входящее в (2.27), с учетом соотношений (2.14):

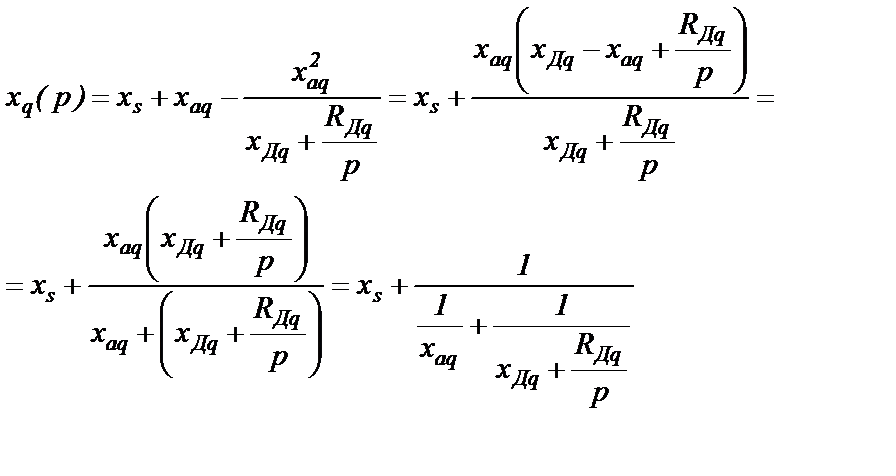(2.28)

Выражению (2.28) соответствует принципиальная электрическая схема на рис.2.7,а.

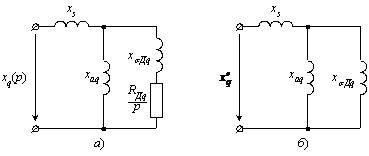
Рисунок 2.7 - Сопротивления СГ по поперечной оси q

Если скорость изменения тока i_q(t) бесконечно велика (этому допущению практически соответствует начало процесса КЗ), что эквивалентно условию р®¥, если учесть, что р – символ производной, то при р®¥ схема на рис.2.7,а превращается в схему на рис.2.7,б. Сопротивление схемы на рис.2.7,б называется сверхпереходным сопротивлением 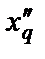СГ по поперечной оси. Смысл этого сопротивления состоит в том, что СГ имеет именно такое сопротивление по поперечной оси в начале процесса КЗ. Согласно схеме на рис.2.7,б имеем

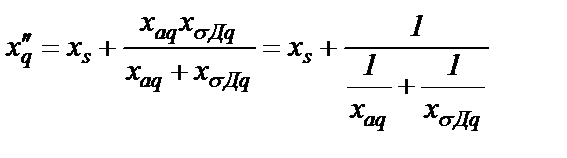(2.29)

Схема на рис.2.7,а напоминает известную Т-образную схему замещения асинхронного двигателя. Поэтому, приведенные выше вычисления и преобразования (2.26…2.28) можно не делать, а можно сразу нарисовать схему на рис.4.1,а, а затем по ней рассчитать операторное сопротивление x_q(p) СГ по поперечной оси. Затем принять р®¥, вычертить схему 4.1б и по ней вычислить сверхпереходное сопротивление .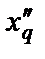

б). Приведение x_q(p) к форме постоянных времени.

Преобразуем x_q(p) (2.27), учитывая при этом соотношения (2.14):

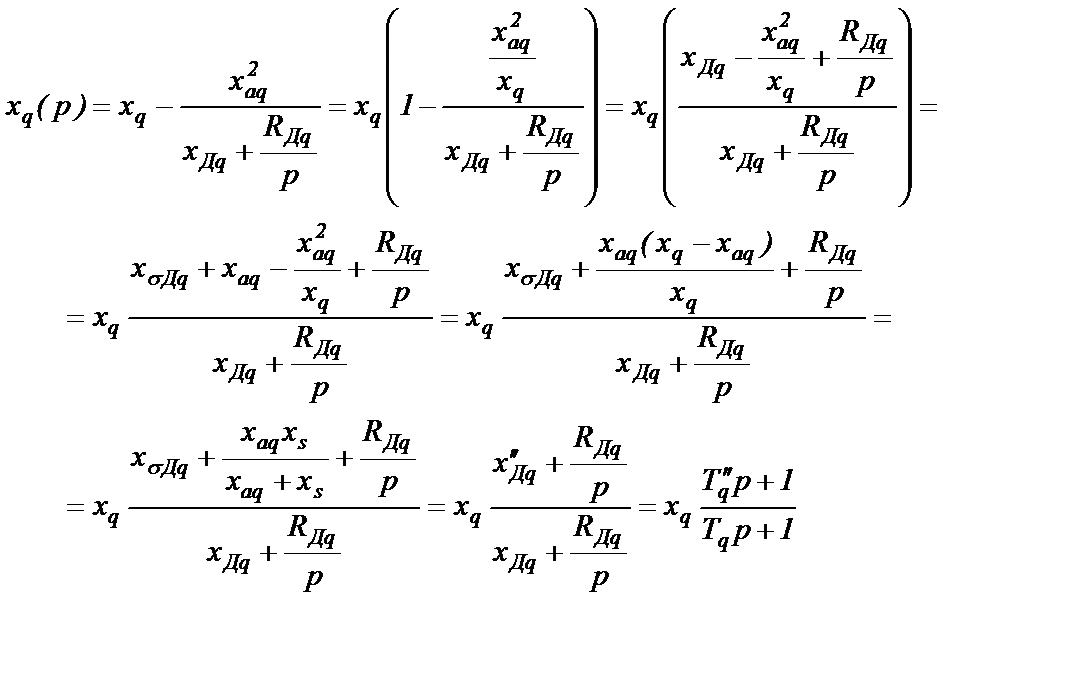(2.30)

Конечное выражение преобразований (2.30) ряд новых величин, пояснения к которым приведено ниже.

Введем понятие "сверхпереходного сопротивления демпферной обмотки СГ по поперечной оси", величина которого определится выражением

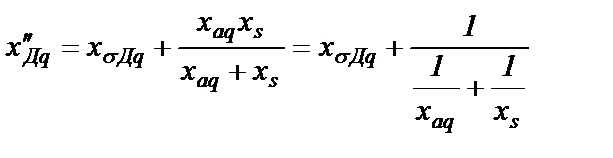(2.31)

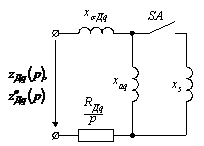
Рисунок 2.8 - Сопротивления демпферной обмотки СГ по оси q

Выражение, стоящее в числителе предпоследнего выражения ряда (2.30), является полным сверхпереходным сопротивлением 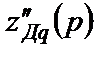демпферной обмотки по поперечной оси и находится оно из схемы, изображенной на рис.2.8. при замкнутом ключе SA или при "замкнутой статорной обмотке". Термин "замкнутой статорной обмотке" является общепринятым в теории переходных процессов синхронных машин. Именно таким будет сопротивление демпферной обмотки в самом начале процесса КЗ.

Выражение, стоящее в знаменателе того же выражения является полным сопротивлением z_Дq(p) демпферной обмотки по поперечной оси и находится оно из схемы на рис.2.8 при разомкнутом ключе SA или при "разомкнутой статорной обмотке". Именно таким будет сопротивление демпферной обмотки спустя несколько периодов от начала КЗ.

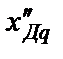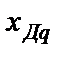Результатом деления и на 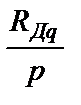являются две постоянные времени:

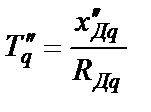- сверхпереходная постоянная времени СГ по поперечной оси, которая характеризует интенсивность затухания поперечной составляющей i_q тока демпферной обмотки в начале процесса КЗ при замкнутом статоре;

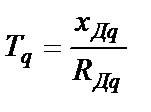– собственная постоянная времени СГ по поперечной оси, которая характеризует интенсивность затухания поперечной составляющей i_q тока демпферной обмотки с того момента, когда апериодический ток в статоре считается затухшим.

Очевидно, что 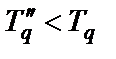. Для существующих СГ фактически .

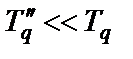Вместо выполнения громоздких выводов (2.26…2.28, 2.30) для вычисления постоянных времени 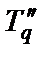и T_q необходимо, как видно из изложенного, составить схему СГ (рис.2.8) по поперечной оси со стороны демпферной обмотки и в зависимости от положения ключа SA вычислить индуктивные сопротивления 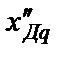и 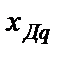, а затем – постоянные времени 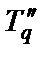и T_q.

Вопросы для самоконтроля

1. Перечислите и дайте характеристику принятым условиям описания процесса короткого замыкания.

2. Приведите систему уравнений Парка-Горева для расчета режима КЗ и перечислите этапы расчета.

3. Приведите вывод сопротивления x_q(p) в исходной форме.

4. Приведите преобразование исходного выражения x_q(p) к форме сопротивлений.

5. Приведите схемы для расчета по ним операторного сопротивления x_q(p) и сверхпереходного сопротивления .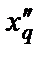

6. Приведите преобразование исходного выражения x_q(p) к форме постоянных времени.

7. Приведите схему для расчета по ней сверхпереходного сопротивления 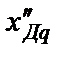и поясните его физический смысл.

8. Поясните физический смысл собственной T_q и сверхпереходной 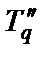постоянных времени СГ по поперечной оси.

Литература [1-9]

2.4 Операторное сопротивление х_d(р) СГ по оси d

Расчет операторного сопротивления x_d(p) СГ по продольной оси

В принципе, при расчете x_d(p) можно идти через преобразования формул, так как это было проделано выше для поперечной оси, и получить выражение вида

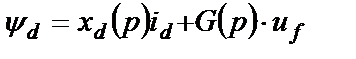, (2.32)

где G(p) – операторная проводимость по продольной оси.

Однако выводы для продольной оси гораздо сложнее и более громоздкие в сравнении с выводами для поперечной оси. Гораздо проще можно определить x_d(p) по эквивалентным электрическим схемам, составленным по правилам, установленным при расчетах x_q(p).

а). Приведение x_d(p) к форме сопротивлений.

Эквивалентные схема для определения x_d(p) приведена на рис.2.9,а, а для расчета сверхпереходного 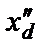и переходного 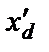сопротивлений – на рис.2.9,б и 2.9,в, соответственно.

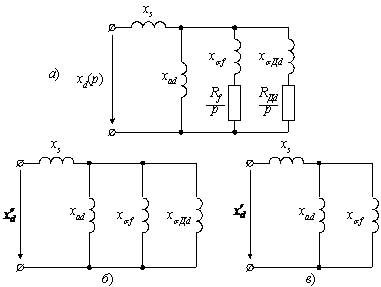
Рисунок 2.9 - Сопротивления СГ по продольной оси d

В соответствии с рис.2.9,а операторное сопротивление по продольной оси определится выражением

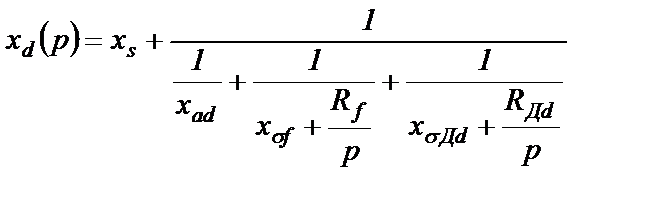(2.33)

Сверхпереходное сопротивление в соответствии с рис.2.9,б

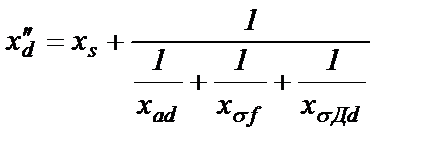(2.34)

Физический смысл сверхпереходного сопротивления состоит в том, что таким будет сопротивление СГ со стороны статора в самом начале процесса КЗ, когда и в обмотке возбуждения, и в демпферной обмотке возникают свободные токи и скорость их изменения максимальна. Отображением максимальной скорости изменения токов в обмотках ротора является принятие значения символа производной р в схеме 2.9,а равным бесконечности: р®¥.

Переходное сопротивление в соответствии с рис.2.9,в равно

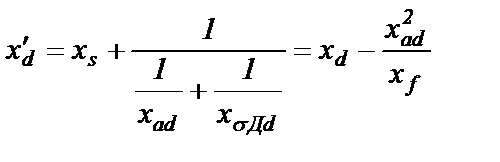(2.35)

Физический смысл переходного сопротивления состоит в том, что таким будет сопротивление СГ со стороны статора с того момента, когда свободные токи в демпферной обмотке стали равными нулю (оператор р при сопротивлении R_Дd становится равным нулю: р=0), а в обмотке возбуждения свободные токи еще присутствуют, изменяясь с достаточно большой скоростью нулю (оператор р при сопротивлении R_f остается равным бесконечности: р®¥).

Такой метод вычислений сопротивлени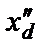й и 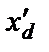имеет то подтверждение, что в существующих СГ свободные токи в демпферной обмотке затухают намного быстрее, чем в обмотке возбуждения.

б). Приведение x_d(p) к форме постоянных времени.

Операторное сопротивление имеет вид

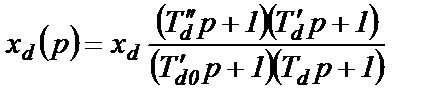(2.36)

Постоянные времени определяются из схем обмоток ротора по продольной оси (аналогично схеме на рис.2.8) с учетом сопротивления взаимной индукции и индуктивного сопротивления статора. Две постоянных времен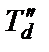и и 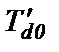рассчитываются с использованием схемы демпферной обмотки, а две другие 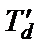и 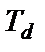– из схемы обмотки возбуждения.

Сверхпереходная постоянная времени 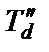СГ по продольной оси характеризует интенсивность затухания продольного тока i_d в первый момент процесса КЗ, когда еще существуют свободные токи во всех трех обмотках, расположенных на продольной оси d (рис.2.6). Эта постоянная времени определяется с использованием схемы, приведенной на рис.2.10,а, по которой рассчитывается сопротивление СГ со стороны демпферной обмотки.

Сверхпереходное индуктивное сопротивление демпферной обмотки по продольной оси и сверхпереходная постоянная времени согласно схеме 2.10,а будут равны

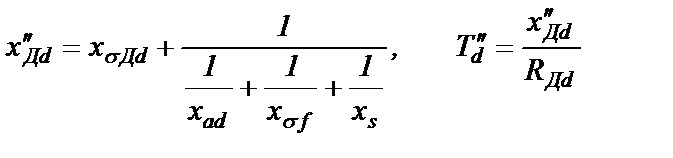(2.37)

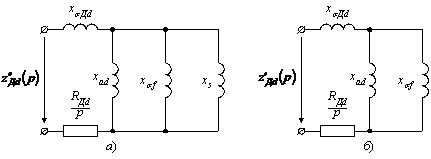
Рисунок 2.10 - Сопротивления демпферной обмотки СГ по оси d

Переходная постоянная времени 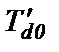демпферной обмотки по продольной оси характеризует интенсивность затухания продольного тока i_d с того момента процесса КЗ, когда еще существуют свободные токи в обмотках демпферной и возбуждения, но уже затухли свободные токи в обмотке статора. Эта постоянная времени определяется с использованием схемы, приведенной на рис.2.10,б, по которой рассчитывается сопротивление СГ со стороны демпферной обмотки при указанных условиях, а именно – цепь статора разомкнута, а обмотки возбуждения замкнута.

Переходное индуктивное сопротивление демпферной обмотки по продольной оси и переходная постоянная времени согласно схеме на рис.2.10,б будут равны

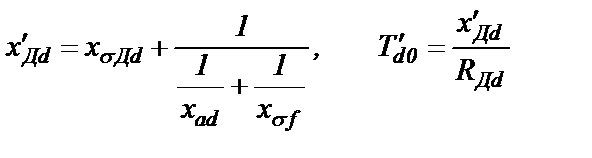(2.38)

Переходная постоянная времени 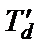СГ по продольной оси характеризует интенсивность затухания продольного тока i_d с того момента процесса КЗ, когда уже затухли свободные токи в демпферной обмотке, но еще существуют свободные токи в обмотках статора и обмотки возбуждения. Эта постоянная времени определяется с использованием схемы, приведенной на рис.2.11,а, по которой рассчитывается сопротивление СГ со стороны обмотки возбуждения.

Переходное индуктивное сопротивление обмотки возбуждения и переходная постоянная времени согласно схеме на рис.2.11,а будут равны

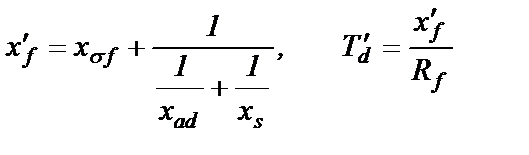(2.39)

Собственная постоянная времени обмотки возбуждения T_d0 характеризует интенсивность затухания продольного тока i_d с того момента, когда затухли свободные токи в как в демпферной обмотке, так и в статоре. Эта постоянная времени определяется из рис.2.11,б

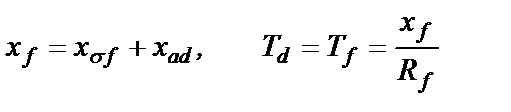(2.40)

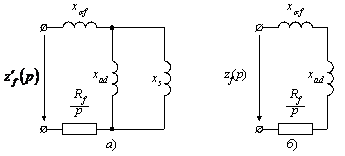
Рисунок 2.11 - Сопротивления обмотки возбуждения СГ по оси d

При составлении схем на рис.2.10 и 2.11 использовался тот опытный факт, что в существующих СГ самое короткое время затухают свободные токи в демпферной обмотке, практически на порядок дольше затухают свободные токи в обмотке статора и еще на один-два порядка больше время затухания свободных токов в обмотке возбуждения.

Выражение G(p), входящее в (2.32) рассчитывать не будем, так как при определении токов КЗ при условии неизменности напряжения возбуждения (u_f=const) в течение всего времени КЗ G(p) не будет присутствовать в конечном выражении тока КЗ.

Вопросы для самоконтроля

1. Приведите схемы для расчета по ним операторного сопротивления x_d(p), сверхпереходного 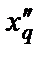и переходного 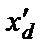сопротивлений. Составьте по схемам выражения названных сопротивлений.

2. Приведите схемы для расчета по ним постоянных времен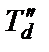и и 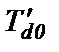. Поясните физический смысл указанных постоянных времени.

3. Приведите схемы для расчета по ним постоянных времен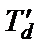и и 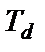. Поясните физический смысл указанных постоянных времени.

Литература [1-9]

2.5 Изображение i_кз(р) тока короткого замыкания

Изображение тока КЗ состоит из двух токов – тока КЗ i_d(р) по продольной оси d и тока i_q(р) по поперечной оси q. Вычисление этих токов выполним в следующей последовательности:

Сначала определяем начальные значения всех переменных, входящих в УПГ (2.12) и выражения потокосцеплений (2.14). До момента КЗ режим работы СГ был установившийся и, поэтому, все производные в уравнениях системы (2.12) были равны нулю. Также нужно учесть условия, заданные выражениями (2.1…2.3), а также равенство нулю начальных значений тока КЗ, так как до КЗ генератор работал вхолостую

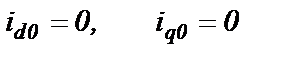(2.41)

Из (2.12) при отмеченных условиях получаем систему уравнений, пригодную для определения начальных условий для всех переменных

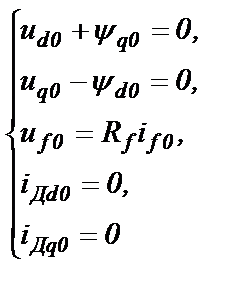(2.42)

Из (2.14) с учетом (2.42) получим

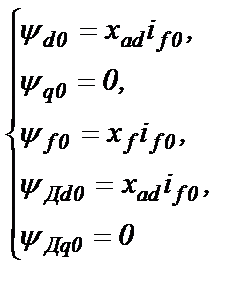(2.43)

Из уравнений систем (2.42) и (2.43) находим начальные значения сигналов до КЗ

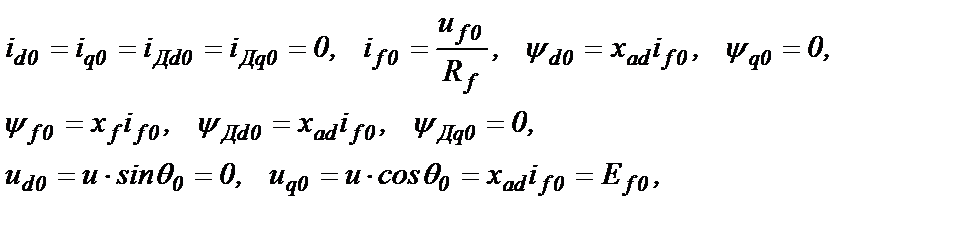(2.44)

где E_f0 – э.д.с. холостого хода СГ.

Затем вычисляем значения тех же сигналов (токов, напряжений и потокосцеплений СГ) в первый момент КЗ. Согласно первого закона коммутации значения всех токов и потокосцеплений останутся теми же, что и до момента КЗ и, следовательно будут такими же, как определено выражениями (2.44). Напряжения же могут измениться скачком до значений, определяемых условиями (2.20) и (2.22).

Далее все расчеты будем вести в отклонениях сигналов от их начальных значений. В частности для напряжений, являющихся для данной задачи расчета тока КЗ входными сигналами, изменения будут следующими по величине

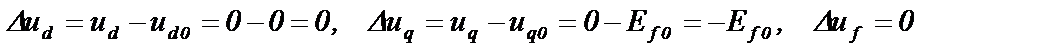(2.45)

В соответствии с допущениями, принятыми при расчете тока КЗ система (2.12) будет линейной и к ней применима линеаризация без изменения вида уравнений.

Из (2.12) берем первые два уравнения, выраженные в отклонениях, и переводим их в операторную форму записи

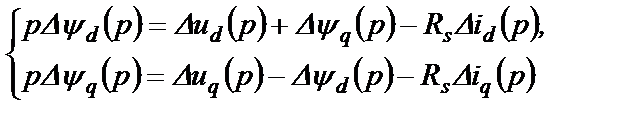(2.46)

В отклонениях записываем также (4.6) и (4.16)

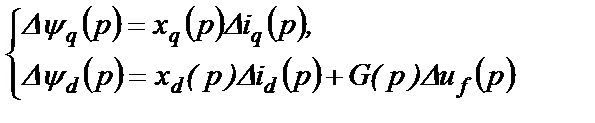(2.47)

Изображения от (2.45) будут следующими

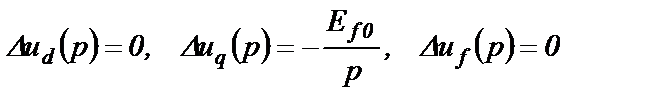(2.48)

Следовательно, из (2.46) и (2.47) получим

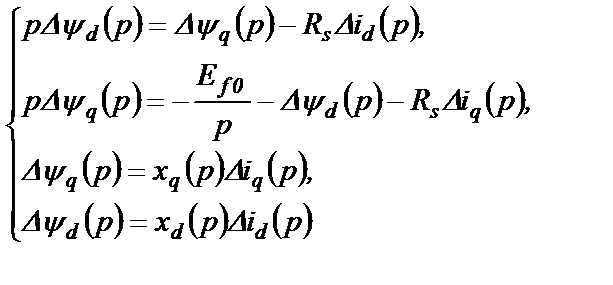(2.49)

Система (2.49) из 4-х уравнений содержит четыре неизвестных сигнала: Dy_d(p), Dy_q(p), Di_d(p) и Di_q(p) и, поэтому из нее может быть найден любой из этих сигналов. Определим из нее только токи Di_d(p) и Di_q(p).

Обратим внимание на то, что начальные значения токов i_d и i_q равны нулю (см. (2.44)). Поэтому величины отклонения токов Di_d(p) и Di_q(p) являются одновременно абсолютными значениями Di_d(p) и Di_q(p), что позволяет опустить в написании токов знак D .

Исключаем из (4.33) переменные Dy_d(p) и Dy_q(p):

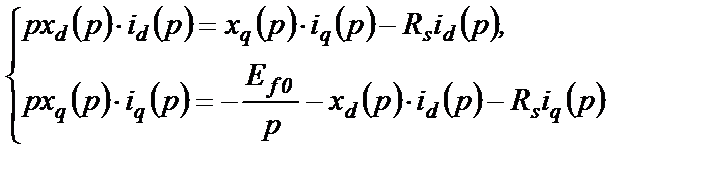(2.50)

Обозначим полные входные операторные сопротивления СГ по продольной и поперечной осям как

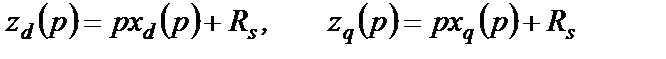(2.51)

Тогда система (2.50) примет вид

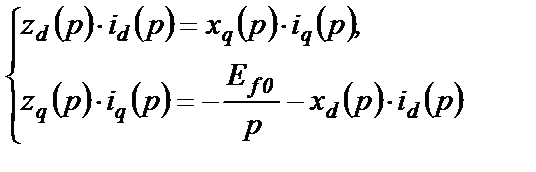(2.52)

Исключаем из (2.52) i_q(p)

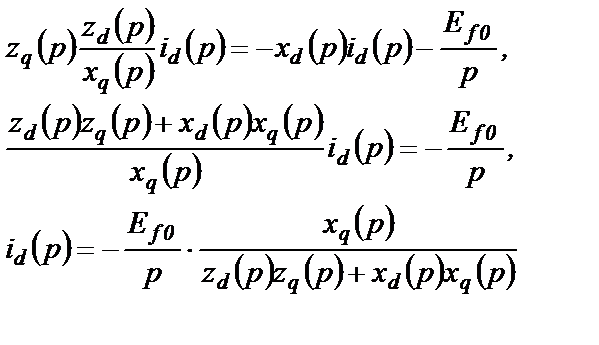(2.53)

Из совместного решения 1-го уравнения системы (4.36) и последнего уравнения системы (4.37) находим

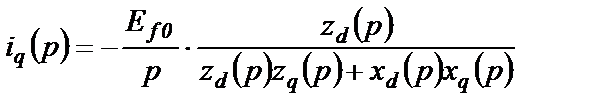(2.54)

Выражения (2.53) и (2.54) – это изображения составляющих тока КЗ по осям d и q. Преобразуем знаменатели выражений (2.53) и (2.54)

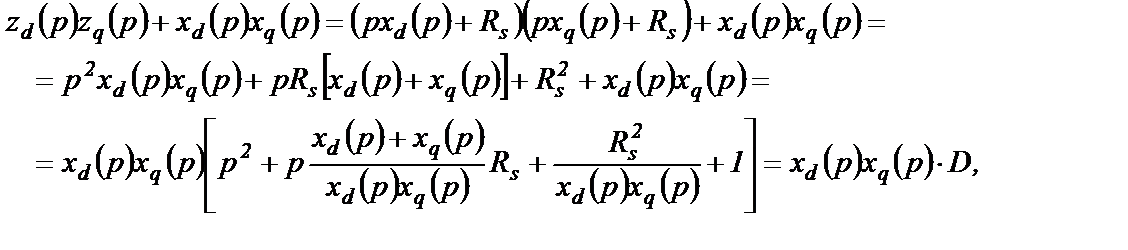
где D – обозначение выражения, заключенного в квадратные скобки.

Составляющие i_d(p) и i_q(p) изображения тока КЗ примут вид

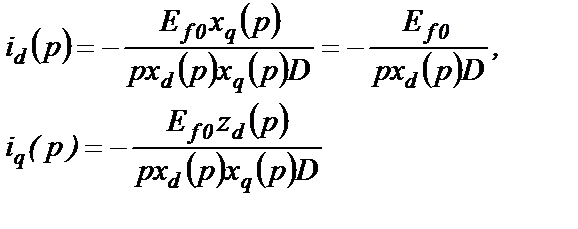(2.55)

Вопросы для самоконтроля

1. Как рассчитать начальные условия для переменных, входящих в уравнения Парка-Горева СГ?

2. Составьте систему операторных уравнений в отклонениях процесса КЗ. При каких условиях сигналы отклонения токов могут быть заменены на сигналы абсолютных значений токов?

3. Выведите выражения изображений составляющих ток КЗ по осям d и q.

Литература [1-9]

2.6 Оригинал i_кз(t) тока короткого замыкания. Расчет ударного тока

В принципе по изображениям (2.55) можно рассчитать оригиналы токов. Однако вычисления будут достаточно сложными из-за того, что характеристическое уравнение изображений токов имеют 5-й порядок и корни аналитически не определяются. Поэтому далее принимаем ряд упрощений, допустимость которых подтверждена практикой – погрешность определения тока КЗ с учетом допущений не превышает 5%.

Допущение 1. В z_d(p), входящем в числитель выражения тока i_q(p), полагаем R_s=0. Следовательно

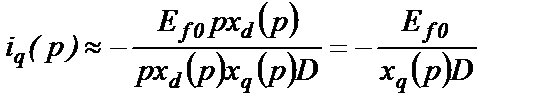(2.55)

Допущение 2. В выражении D вместо операторных сопротивлений x_d(p) и x_q(p) будем использовать сверхпереходные сопротивления 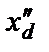и 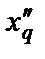, т.е.

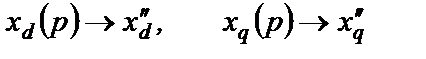(2.56)

Такая замена допустима для начального периода процесса КЗ. Имеем

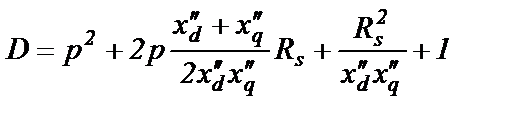(2.57)

Выражение

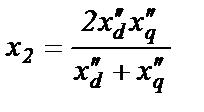(2.58)

называется индуктивным сопротивлением обратной последовательности фаз СГ.

Величина

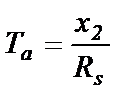(2.59)

называется постоянной времени статорной обмотки и она определяет темп затухания тока КЗ в цепи статора на начальных его этапах. С учетом (2.58) и (2.59) получим

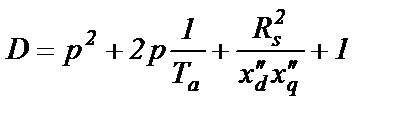(2.60)

Допущение 3. Для существующих СГ справедлива замена

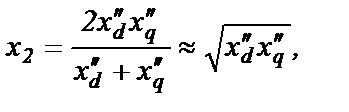(2.61)

так как погрешность от такой замены невелика.

Тогда

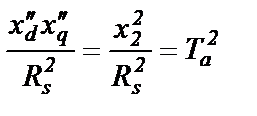
и 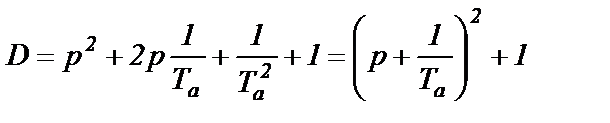(2.62)

Именно это определение D будем подставлять в выражения (2.55) и (2.56).

Продолжим вычисления токов i_d(p) и i_q(p) , подставив в i_d(p) значение x_d(p) в форме постоянных времени (2.36), а в i_q(p) значение x_q(p) также в форме постоянных времени (2.30). В итоге получим

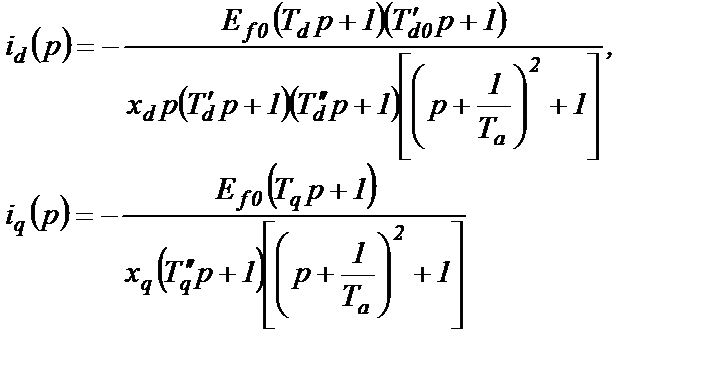(2.63)

Характеристические полиномы (знаменатели) выражений (4.49) представлены в виде произведения величин типа: р, (Тр+1) и 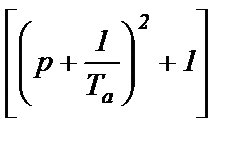, и, поэтому, выражения (2.63) могут быть представлены в виде суммы дробей типа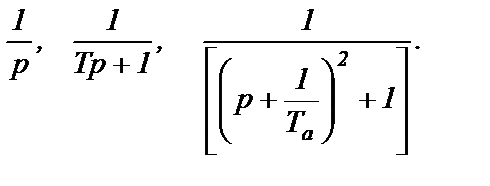

В соответствии с таблицей преобразований Лапласа этим дробям соответствуют оригиналы:

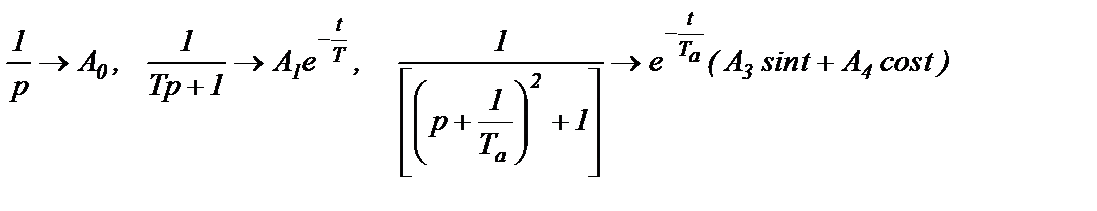(2.64)

Поэтому можно, исходя из (2.63), записать в общем виде выражения оригиналов токов

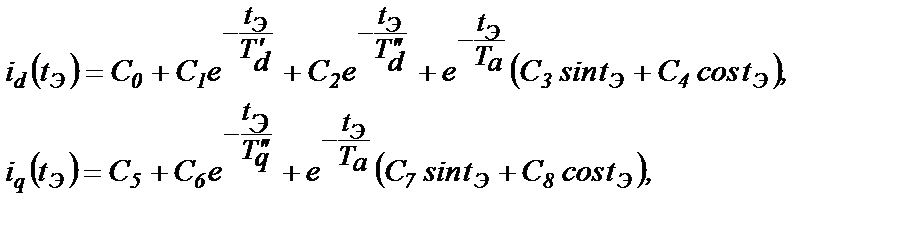(2.65)

где С₀…С₈ – постоянные интегрирования, определяемые из начальных условий;

t_э – электрические секунды.

В выражении (2.65) все постоянные времени также выражены в электрических секундах.

Оригинал тока КЗ, например, фазы А будет следующим

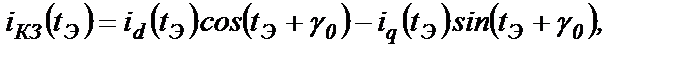
а в физических секундах

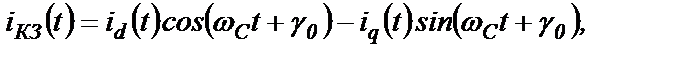(2.66)

причем 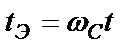(2.67)

Качественно график тока i_КЗ(t) выглядит так, как показано на рис.2.12 Форма графика тока КЗ зависит от начальной фазы g₀ напряжения фазы А СГ.

Практика и расчеты показывают, что самый тяжелый режим КЗ, сопровождающийся наибольшим мгновенным значением тока, наблюдается при g=-5⁰…+5⁰, т.е. при g»0⁰. Наибольшее мгновенное значение тока КЗ называется ударным током. Ударный ток наступает при t_э=w_сt»p.

По величине ударного тока проводится проверка на динамическую устойчивость автоматических выключателей сети. Следовательно, важнейшим для практики является определение простейшим способом величины этого тока.

В соответствии с изложенным, ударный ток определится выражением

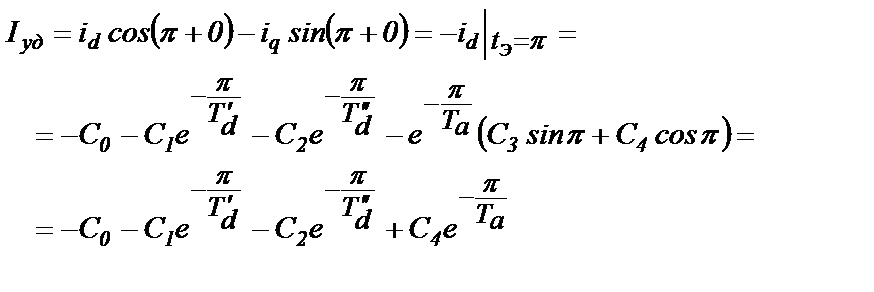(2.68)

Вычисления постоянных интегрирования С₀, С₁, С₂ и С₄ и их подстановка в (2.68) дают следующее выражение для определения ударного тока

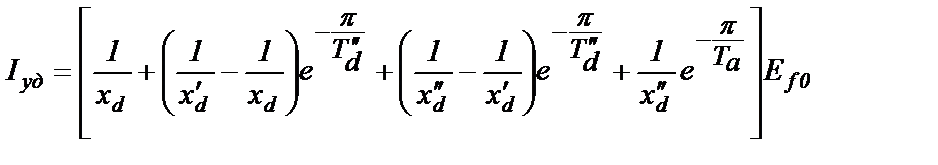(2.69)

Для существующих СГ справедливы неравенства

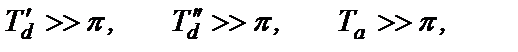
что позволяет принять

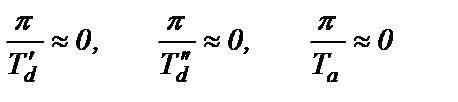(2.70)

С учетом условий (2.70) ударный ток определится приближенно выражением

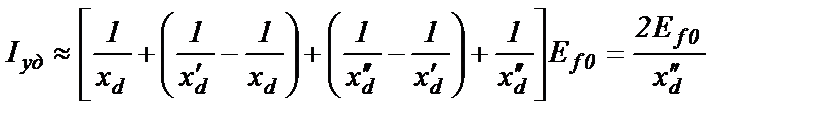(2.71)

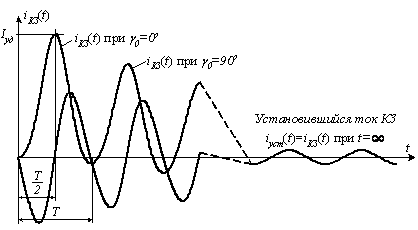
Рисунок 2.12 - Графики тока короткого замыкания СГ

Если не принимать условия (2.70), а вычислить (2.69) при значениях 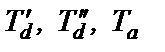, которые характерны для существующих СГ, то для ударного тока получим приближенную формулу

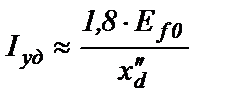(2.72)

Этой формулой пользуются на практике.

Типовое значение ударного тока составляет 10…15 крат номинального тока статора СГ. Установившееся значение тока короткого замыкания составляет всего 1,5…2 крата от номинального тока статора СГ.

Вопросы для самоконтроля

1. Какие допущения принимаются при расчете оригинала составляющих тока КЗ в осях d и q?

2. Как принятые допущения повлияли на трудоемкость и погрешность расчета тока КЗ?

3. Как рассчитать ток короткого замыкания фазы синхронного генератора?

4. При каких начальных условиях рассчитывается ударный ток короткого замыкания?

5. Приведите точные и приближенные выражения ударного тока короткого замыкания.

Литература [1-9]