Уравнения Парка-Горева. Система относительных единиц

Дальнейшие упрощения дифференциальных уравнений СГ связаны с приведением всех обмоток СГ к обмоткам статора и с введением относительных единиц для электрических и механических характеристик СГ в соответствии с выражениями

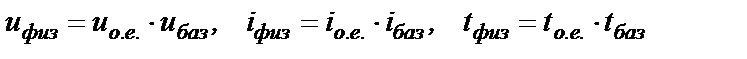и т.д., (2.11)

где индексом "баз" обозначены базисные величины.

За базисные величины принимаются амплитуды номинальных значений напряжения, тока, частота сетевого напряжения и т.д. Преимущество дифференциальных уравнений в относительных единицах в том, что упрощается выбор численного метода решения системы дифференциальных уравнений СГ, а также возможно сравнение между собой процессов в генераторах разных мощностей. Такая возможность сравнения является основой физического моделирования. С формальной точки зрения переход от физической системы уравнений (3.5) к уравнениям в относительных единицах представляет собой замену одних переменных другими.

Изложенные выше идеи простого описания СГ, а также учет уравнений движения ротора СГ под действием момента приводного двигателя (дизеля) и электромагнитного момента сопротивления генератора, приводят к системе уравнений Парка-Горева (сокращенно – УПГ) следующего вида:

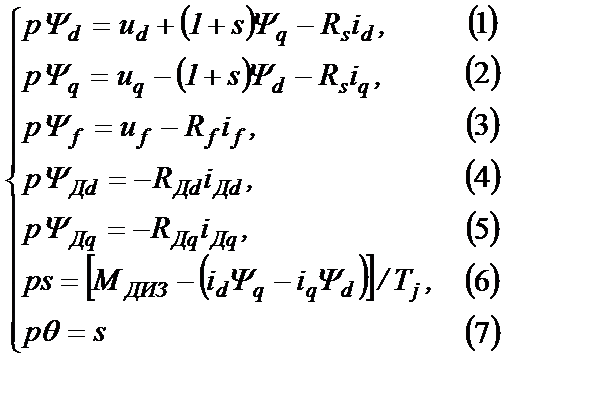(2.12)

где u_d и u_q - напряжения статора, которые определяются выражениями (2.9);

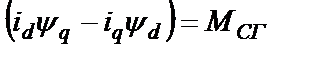- электромагнитный момент синхронного генератора, создающий сопротивление вращению;

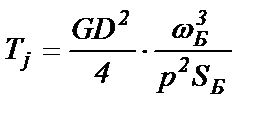- механическая постоянная времени агрегата "СГ + приводной двигатель", имеющих суммарный маховый момент GD²/4;

w_Б – базисная частота, равная частоте напряжения сети w_с;

р – число пар полюсов обмотки статора физического СГ;

S_Б – базисная мощность СГ, равная его номинальной полной мощности;

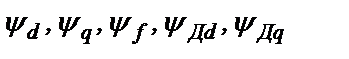- потокосцепления обмоток модельного СГ, которые определяются выражениями

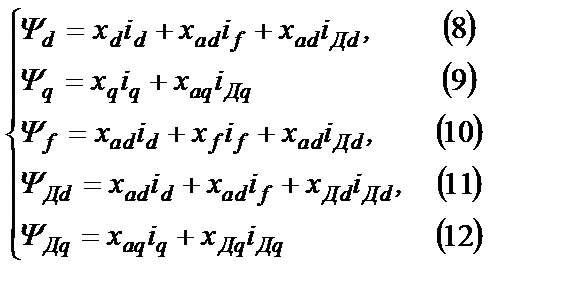(2.13)

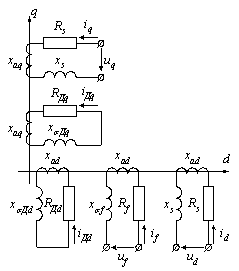
Рисунок 2.6 - Развёрнутая схема обмоток СГ в осях d и q ротора

В выражениях (8)…(12) системы (2.13) индуктивные сопротивления определяются из рис.2.6, являющегося аналогом рис.2.5.

На рис.2.6 обозначены сопротивления:

x_ad – сопротивление взаимной индукции обмоток СГ по продольной оси d;

x_aq - сопротивление взаимной индукции обмоток СГ по поперечной оси q;

x_s – индуктивное сопротивление рассеяния обмоток статора;

x_sf – индуктивное сопротивление рассеяния обмотки возбуждения;

x_sДd, x_sДq – индуктивные сопротивления рассеяния демпферных обмоток по осям d и q;

R_s, R_f, R_Дd, R_Дq – активные сопротивления обмоток СГ.

Полные индуктивные сопротивления обмоток равны сумме индуктивных сопротивлений взаимной индукции и индуктивного сопротивления рассеяния:

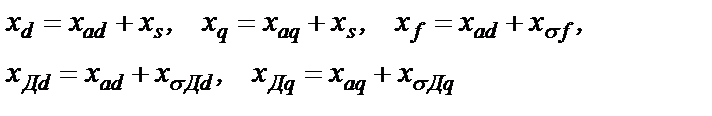(2.14)

Время t в УПГ измеряется в электрических секундах, причем

1 секунда физическая = 314 секунд электрических (2.15)

Если в результате решения УПГ получены, например, токи i_d и i_q, то ток i_A фазы А физического генератора определится выражением

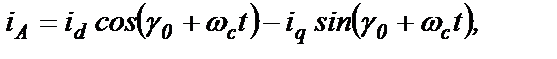(2.16)

где w_с – частота тока в сети;

t – физическое время;

g₀ – начальный угол (при t=0) между осями d и a (см. рис.2.5).

Вращающий момент дизеля М_ДИЗ в системе (2.12) должен быть выражен в относительных единицах

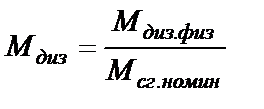(2.18)

Из системы (2.14) токи обмоток выражаются через потокосцепления по формулам

(2.19)

где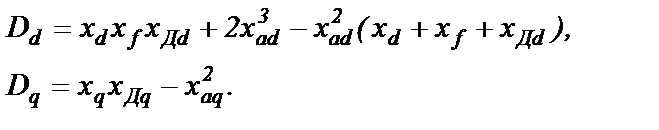

При моделировании процессов в СГ по УПГ (2.12) в качестве переменных интегрирования используются потокосцепления 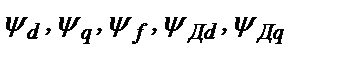. Поэтому в (3.12) все токи должны быть заменены согласно (3.19). При решении УПГ будут получены значения потокосцеплений 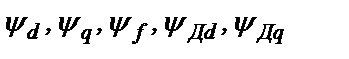. Пересчет потокосцеплений в токи выполняется по формулам (2.19), а переход к физическим переменным осуществляется по формулам типа (2.17).

Вопросы для самоконтроля

1. Приведите уравнения Парка-Горева.

2. Приведите выражения потокосцеплений обмоток СГ.

2. Приведите развернутую схему обмоток СГ в осях его ротора.

3. Приведите выражения величин модели СГ в относительных единицах.

4. Как рассчитать токи физических обмоток статора через токи статора, определенные в осях d и q?

Литература [1-9]