Методика моделирования нелинейных ЭМС на аналоговых решающих элементах
В задачах моделирования возникает необходимость в выполнении нелинейных математических операций, таких как, умножение, деление, воспроизведение нелинейности произвольного вида. Так в электроприводе переменного тока с векторным управлением для определения модуля вектора потокосцепления ротора Ψ2 используются нелинейные операции возведения в квадрат и извлечение квадратного корня: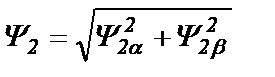 
. Операция умножения двух сигналов х и у может быть реализована на двух блоках возведения в квадрат:
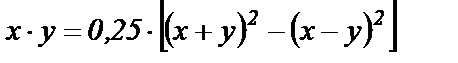
Элементная база для моделирования нелинейностей
Для моделирования любой однозначной нелинейности используются диодные ячейки, представленные на рис.1.7, и еще две линейные ячейки, приведенные на рис.1.8.
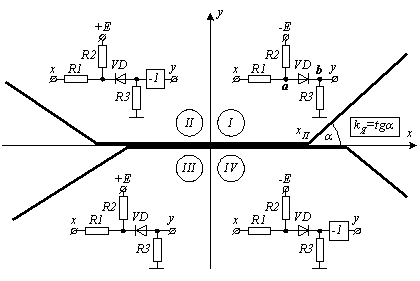
Риунок.1.7 - Принципиальные электрические схемы диодных ячеек
Проходные характеристики диодных ячеек, устанавливаящие связь между входным х и выходным у сигналами, состоят из двух отрезков прямых (рис.1.7). Рассмотрим подробнее и рассчитаем диодную ячейку для первого квадранта. Для рассчетов используем эквивалентную схему этой диодной ячейки, приведенную на рис.1.9.
Катод диода VD (точка b схемы) заземлен через резистор R3 и, поэтому, находится под нулевым потенциалом - напряжение в точке b относительно земли. Диод может быть открытым или закрытым в зависимости от потенциала на его аноде (точке а). Потенциал в точке а создается двумя источниками: отрицательным опорным напряжением -Е и положительным входным сигналом х. Потенциал точки а определим методом двух узлов:
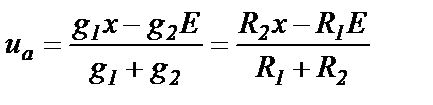(1.23)
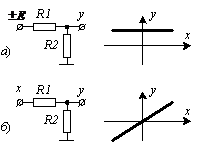
Рисунок 1.8 - Принципиальные электрические схемы линейных ячеек
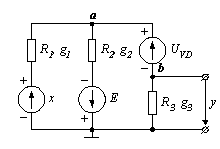
Рисунок 1.9 - Расчётная схема диодной ячейки 1-го квадранта
Диод VD будет закрыт, если напряжение ua на его аноде будет меньше 0,4…0,5 В (для полупроводниковых кремниевых диодов напряжение открытия UVD составляет »0,4…0,5 В). Входное напряжение х, при котором потенциал точки а становится равным UVD и диод VD открывается, называется пороговым хП. С учетом (1.23) пороговое значение определяется расчетом:
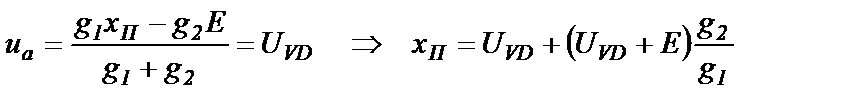
При открытом диоде межузловое напряжение в схеме на рис.1.9 равно
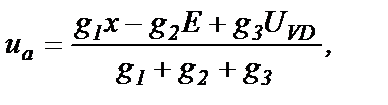
а выходное
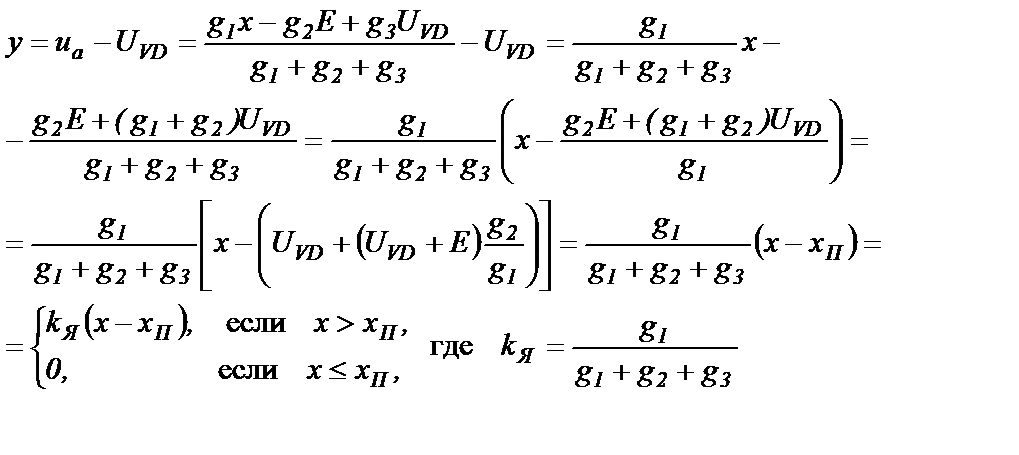(1.24)
Методика моделирования нелинейностей
Методику рассмотрим на примере графика нелинейности, приведенной на рис.1.10. Оси графиков размечены в вольтах – V.
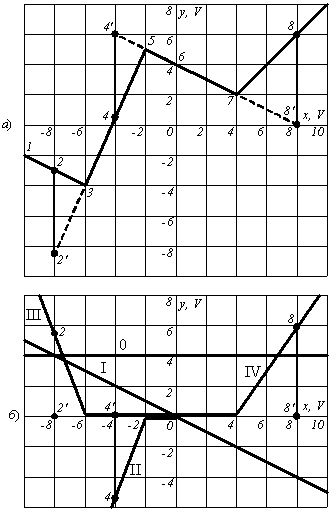
Рисунок 1.10 - Исходная нелинейность (а) и её разложение на типовые характеристики (б)
Разложение исходной нелинейности на типовые характеристики, которые приведены на рис.1.7 и рис.1.8, представим в виде последовательности действий:
1. На рис.1.10,а определяем точку пересечения графика нелинейности с осью у. Это точка 6 и в ней у=4 V. На рис.1.10,б проводим отрезок 0 постоянного уровня у0=4 V. Отрезок 0 будет реализован с помощью схемы, приведенной на рис.1.8,а.
2. На рис.1.10,б проводим отрезок I с наклоном, равным наклону отрезка 5-6-7 на рис.1.10,б. Отрезок I будет реализован с помощью схемы, приведенной на рис.1.8,б, дополненной инвертором. Коэффициент наклона линии I равен
,
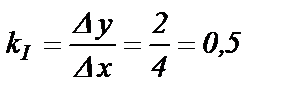где при произвольно заданном изменении сигнала х на величину 4 V определенное из графика I изменение сигнала у составляет 2 V.
3. Непосредственно к отрезку 5-6-7 примыкают два отрезка 3-4-5 и 7-8. Для определенности, начнем с отрезка 3-4-5. Если бы не было ячейки набора нелинейности, воспроизводящей отрезок 3-4-5, то при х=-4 V значению у соответствовала бы точка 4'. С добавлением отрезка 3-4-5 при том же х=-4 V значение у переместится в току 4. Следовательно, ячейка , воспроизводящая отрезок 3-4-5 должна повернуть ход графика нелинейности (рис.1.10,а) против часовой стрелки так, чтобы при х=-4 V опускание графика было бы равно длине отрезка 4-4'. Таким графиком должен быть график II на рис.1.10,б, и его можно реализовать с помощью диодной ячейки третьего квадранта (рис.1.7). Параметры графика II:
- пороговое напряжение хП,II=-2 V;
- коэффициент наклона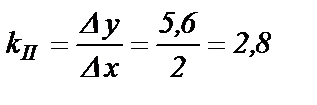 
.
4. Непосредственно к отрезку 3-4-5 примыкает два отрезок 1-2-3. Ячейка, реализующая этот отрезок, должна поворачивать график по часовой стрелке с тем условием, что х=-8 V значение у будет поднято над осью х на величину, равную отрезку 2-2'. Таким графиком должен быть график III на рис.1.10,б, и его можно реализовать с помощью диодной ячейки второго квадранта (рис.1.7). Параметры графика III:
- пороговое напряжение хП,III=-6 V;
- коэффициент наклона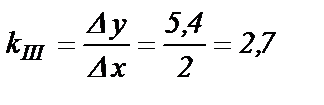 
.
5. Аналогичными рассуждениями устанавливаем, что для реализации отрезка 7-8 на рис.1.10,а необходимо диодной ячейкой воспроизвести график IV, что на рис.1.10,б и такой является диодная ячейка первого квадранта (рис.1.7). Параметры графика IV:
- пороговое напряжение хП,IV=4 V;
- коэффициент наклона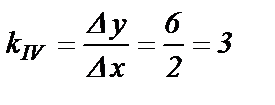 
.
Если, изменяя значение х от -10 V до +10 V, сложить графики 0, I, II, III и IV, что на рис.1.10,б, то их суммой будет график нелинейности, приведенный на рис.1.10,а. Обратно следует, что для воспроизведения графика исходной нелинейности, приведенной на рис.1.10,а достаточно с помощью ячеек, приведенных на рис.1.7 и рис.1.8, воспроизвести графики 0, I, II, III и IV, что на рис.1.10,б, и сложить с использованием многовходового сумматора (рис.1.1) выходные сигналы этих ячеек.
Вопросы для самоконтроля
1. Поясните принцип действия и вид проходных характеристик диодных ячеек.
2. Приведите расчет проходной характеристики диодной ячейки.
3. Поясните принцип представления графика произвольной нелинейности в виде суммы типовых графиков.
4. Как рассчитываются параметры линейных ячеек из процедуры разложения исходного графика нелинейности на типовые?
5. Как рассчитываются параметры диодных ячеек из процедуры разложения исходного графика нелинейности на типовые?
Литература [1-9]