Методы аналогового и цифрового моделирования

Базовые решающие элементы аналоговых моделей

Все виды уравнений могут быть смоделированы на базе многовходовых сумматоров и интеграторов.

Принципиальная схема многовходового сумматора приведена на рис.1.1,а.

Выходной сигнал выражается через входные сигналы следующим образом

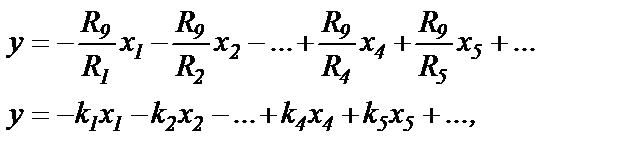(1.1)

где 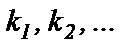- коэффициенты передачи сумматора по входам при условии, что активные проводимости по обоим входам ОУ, вычисленные для цепей протекания постоянного тока, будут равны друг другу:

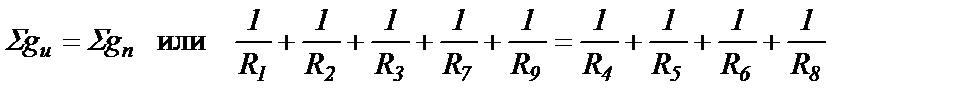(1.2)

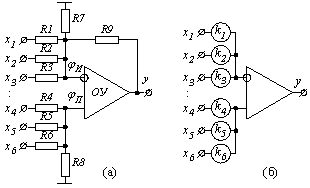
Рисунок 1.1 - Принципиальная (а) и функциональная (б) схемы многоходового сумматора

Доказательство выражения (1.1):

- вычисляем методом двух узлов потенциалы инверсного и прямого входов ОУ:

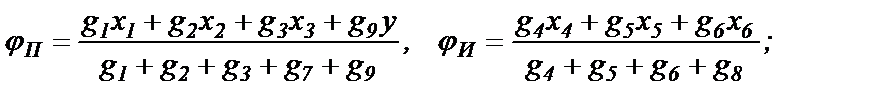(1.3)

- в активном режиме ОУ потенциалы инверсного j_и и прямого j_п входов одинаковы по знаку и величине: j_и=j_п; если принять одинаковыми по величине знаменатели обоих выражений, входящих в систему (1.3), что эквивалентно равенству (1.2), то из равенства числителей выражений (1.3) получим равенство (1.1).

Условие (1.2) является также условием температурной стабильности схемы на базе ОУ.

Принципиальная схема многовходового интегратора приведена на рис.1.2,а.

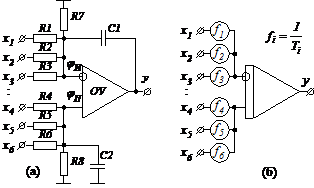
Рисунок 1.2 - Принципиальная (а) и функциональная (б) схемы многоходового интегратора

Конденсаторы С1 и С2 должны быть установлены с одинаковой емкостью, которую обозначим как С.

Выходной сигнал выражается через входные сигналы следующим образом

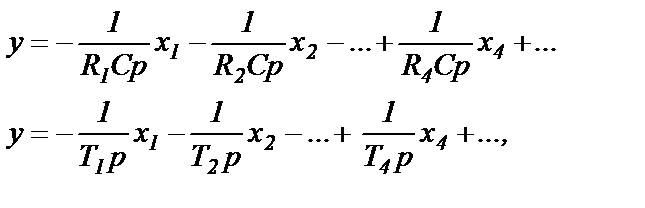(1.7)

где Т₁, Т₂,…- постоянные времени интегратора по соответствующим входам при условии, что активные проводимости по обоим входам ОУ, вычисленные для цепей протекания постоянного тока, будут равны друг другу

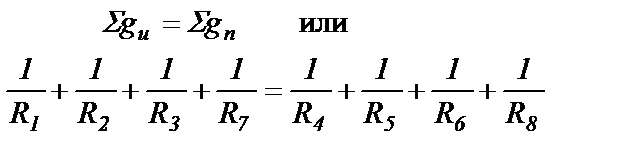(1.8)

Доказательство выражения (1.7):

- вычисляем потенциалы инверсного и прямого входов ОУ

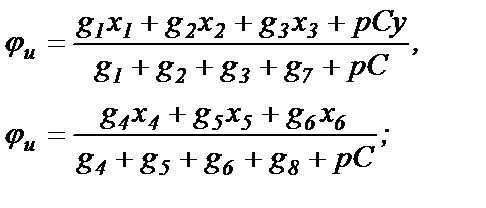(1.9)

- в активном режиме ОУ потенциалы инверсного j_и и прямого j_п входов одинаковы по знаку и величине: j_и=j_п; если принять одинаковыми по величине знаменатели обоих выражений, входящих в систему (1.9), что эквивалентно равенству (1.8), то из равенства числителей выражений (1.9) получим равенство (1.7).

С помощью схем, приведенных на рис.1.1,а и рис.1.2,а, набирается схема решения обыкновенных дифференциальных уравнений. При составлении таких схем на начальных этапах удобно использовать не принципиальные схемы многовходовых сумматоров и интеграторов, а их упрощенные изображения, которые приведены на рис.1.1,б и рис.1.2,б с обозначениями k_i и 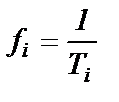входных параметров этих схем.

Вопросы для самоконтроля

1. Приведите вывод выражения (1.1), описывающему работу многовходового сумматора.

2. Приведите вывод выражения (1.7), описывающему работу многовходового интегратора.

3. Зачем выравниваются суммарные активные и реактивные проводимости по обоим входам ОУ в схемах сумматора и интегратора?

Литература [1-9]

Методика моделирования линейных дифференциальных уравнений на аналоговых