Основные характеристики случайной выборки

Лабораторная работа № 3

(подсчет в Excel)

Если набор данных содержит информацию о каждом элементе группы или обо всех возможных измерениях, говорят, что такой набор данных представляет генеральную совокупность. Если измерения проводятся на некотором подмножестве генеральной совокупности или выполняется лишь часть всех возможных измерений, такой набор данных называется выборкой.Метод, когда для описания свойств генеральной совокупности используется выборка, называется методом выборочного обследования.При этом методе используют представительную выборку. Обычно в ее качестве применяется случайная выборка. Для характеристики выборки подсчитывают статистические характеристики

Экспериментально получены измерения некоторой величины

Основные характеристики случайной выборки - student2.ru

Задание № 1

В Excel создадим компьютерную модель решения задачи.

Компьютерная модель = ячейки данных + ячейки вычислений + ячейки результатов

Алгоритм создания компьютерной модели решения задачи

1. Выбрать на листе Excel ячейки и ввести в них данные с пояснениями

2. Последовательно решать задачу: выполнять действия, расчеты и вносить комментарии к ячейкам, в которых производились расчеты

3. Выделить ячейки с результатами (цветом, шрифтом и др.) и написать вывод

Основные характеристики случайной выборки - student2.ru

Рис. Способы размещения компьютерной модели на листе Excel

Подсчитать основные статистические характеристики данной выборки с использованием формул (программирование формул в Excel) для подсчета статистических характеристик (см. ниже).

Рассмотрим на примере подсчета средней арифметической ряда

Действия	Пояснения и визуализация действий
1. Введем исходные данные в столбец
2. С помощью строки состояния подсчитать количество введенных значений и в две соседние ячейки ввести n и количество значений (число)
3.Выделить столбец исходных данных на одну ячейку больше и нажать клавишу . Получим в пустой ячейке сумму выделенного ряда., т.е.
4. Это значение надо разделить на n, т.е. на значение 50. Для этого в ячейку под ячейкой с суммой ряда ввести формулу: =ячейка с суммой/ ячейка, где находится 50 (указать адреса соответствующих ячеек)	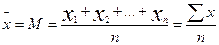Получим значение средней арифметической
5.Для вычисления по некоторым более сложным формулам требуются построения дополнительных рядов по исходному. Поэтому исходные данные мы ввели в столбец.

Задание № 2

В Excel создадим компьютерную модель решения задачи.

Компьютерная модель = ячейки данных + ячейки вычислений + ячейки результатов

Задание № 3

В Excel создадим компьютерную модель решения задачи.

Компьютерная модель = ячейки данных + ячейки вычислений + ячейки результатов

Задание № 4

Провести сравнение статистических характеристик, полученных тремя разными способами в Excel (по арифметическим формулам, по формулам, встроенным в Excel, с помощью пакета). Привести доказательство письменному выводу

Эксцесс

Основные характеристики случайной выборки - student2.ru

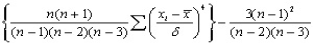
Асимметрия

Основные характеристики случайной выборки - student2.ru

13. Стандартное отклонение Öd²

14. Среднее абсолютное отклонение:

Основные характеристики случайной выборки - student2.ru .

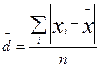15. Коэффициент вариации – отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах:

Основные характеристики случайной выборки - student2.ru .

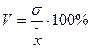Медиана

Медиана разбивает выборку на две равные части. Пятьдесят процентов наблюдений лежит ниже медианы, пятьдесят процентов — выше медианы. Если значение медианы существенно отличается от среднего, то распределение скошено (более подробно см. главу Элементарные понятия).

Мода

Мода — это максимально часто встречающееся значение в выборке. Частота встречаемости также отображается. Если имеется несколько значений с максимальной частотой, то распределение мулътимодалъно. Если каждое значение встречается лишь одни раз, программа делает запись: моды нет (см. электронную таблицу с результатами).

Геометрическое среднее

Геометрическое среднее — это произведение всех значений переменной, возведенное в степень 1/n (единица, деленная на число наблюдений). Геометрическое среднее полезно, например, если шкала измерений нелинейная.

STATISTICA вычисляет геометрическое среднее с помощью логарифмического преобразования: log(геометрическое среднее) = {a[log(xi)]}/n, где x_i— i-е значение, n — число наблюдений. Если переменная содержит отрицательные значения или нуль (0), геометрическое среднее вычислить нельзя.

Гармоническое среднее

Гармоническое среднее иногда используют для усреднения частот. Гармоническое среднее вычисляется по формуле: ГС = n/S( 1/х_i) где ГС — гармоническое среднее, n — число наблюдений, х_i — значение наблюдения с номером i. Если переменная содержит нуль (0), гармоническое среднее вычислить нельзя.

Размах

Размах переменной является показателем изменчивости, вычисляется как максимум минус минимум.

Квартильный размах

Квартальный размах, по определению, равен: верхняя квартиль минус нижняя квартиль (75% процентиль минус 25% процентиль). Так как 75% процентиль (верхняя квартиль) — это значение, слева от которого находятся 75% наблюдений, а 25% процентиль (нижняя квартиль) — это значение, слева от которого находится 25% наблюдении, то квартильный размах представляет собой интервал вокруг медианы, который содержит 50% наблюдений (значений переменной).

Интервал значений признака, содержащий центральные 50% наблюдений выборки, т.е. интервал между 25-м и 75-м процентилями.

Квартильный размах используется вместе с медианой (вместо 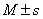Основные характеристики случайной выборки - student2.ru ) для описания данных, имеющих распределение, отличное от нормального.

Асимметрия

Асимметрия — это характеристика формы распределения. Распределение скошено влево, если значение асимметрии отрицательно. Распределение скошено вправо, если асимметрия положительна. Асимметрия стандартного нормального распределения равна 0. Асимметрия связана с третьим моментом и определяется как: асимметрия = n × М³/[(n-1) × (n-2) × s³], где М³равно: 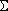Основные характеристики случайной выборки - student2.ru <="" img=""> (х_i-xсреднее_x)³, s³— стандартное отклонение, возведенное в третью степень, n — число наблюдений (СКОС).

Эксцесс

Эксцесс — это характеристика формы распределения, а именно мера остроты его пика (относительно нормального распределения, эксцесс которого равен 0). Как правило, распределения с более острым пиком, чем у нормального, имеют положительный эксцесс; распределения, пик которых менее острый, чем пик нормального распределения, имеют отрицательный эксцесс. Эксцесс связан с четвертым моментом и определяется формулой:

эксцесс = [n × (n+1) × М⁴- 3 × М²× М²× (n-1)]/[(n-1) × (n-2) × (n-3) × s⁴], где M_jравно: 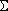Основные характеристики случайной выборки - student2.ru <="" img=""> (х-хсреднее_x, s⁴— стандартное отклонение в четвертой степени, n — число наблюдений (ЭКСЦЕСС).

Стандартная ошибка

Для вычисления стандартной ошибки среднего, используйте одну из следующих формул

= СТАНДАРТНОЕ ОТКЛОНЕНИЕ / КВАДРАТНЫЙ КОРЕНЬ РАЗМЕРА ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ

–ИЛИ-

= STDEV (диапазон значений) и SQRT (Номер)

где:

диапазон значений — данные, используемые для вычисления среднеквадратичного отклонения.

- и -
Номер — это размер всех возможных случайных образцов.

Статистические функцииExcel

СРОТКЛ() - AVEDEV() - Вычисляет среднее абсолютных значений отклонений точек данных от среднего.
СРЗНАЧ() - AVERAGE() - Вычисляет среднее арифметическое аргументов.
СРЗНАЧА() - AVERAGEA() - Вычисляет среднее арифметическое аргументов, включая числа, текст и логические значения.
БЕТАРАСП() - BETADIST() - Определяет интегральную функцию плотности бета-вероятности.
БЕТАОБР() - BETAINV() - Определяет обратную функцию к интегральной функции плотности бета-вероятности.
БИНОМРАСП() - BINOMDIST() - Вычисляет отдельное значение биномиального распределения.
ХИ2РАСП() - CHIDIST() - Вычисляет одностороннюю вероятность распределения хи-квадрат.
ХИ2ОБР() - CHIINV() - Вычисляет обратное значение односторонней вероятности распределения хи-квадрат.
ХИ2ТЕСТ() - CHITEST() - Определяет тест на независимость.
ДОВЕРИТ() - CONFIDENCE() - Определяет доверительный интервал для среднего значения по генеральной совокупности.
КОРРЕЛ() - CORREL() - Находит коэффициент корреляции между двумя множествами данных.
СЧЁТ() - COUNT() - Подсчитывает количество чисел в списке аргументов.
СЧЁТЗ() - COUNTA() - Подсчитывает количество значений в списке аргументов.
СЧИТАТЬПУСТОТЫ() - COUNTBLANK()- Подсчитывает количество пустых ячеек в заданном диапазоне.
СЧЁТЕСЛИ() - COUNTIF() - Подсчитывает количество непустых ячеек, удовлетворяющих заданному условию внутри диапазона.
КОВАР() - COVAR() - Определяет ковариацию, то есть среднее произведений отклонений для каждой пары точек.
КРИТБИНОМ() - CRITBINOM() - Находит наименьшее значение, для которого биномиальная функция распределения меньше или равна заданному значению.
КВАДРОТКЛ() - DEVSQ() - Вычисляет сумму квадратов отклонений.
ЭКСПРАСП() - EXPONDIST() - Находит экспоненциальное распределение.
FРАСП() - FDIST() - Находит F-распределение вероятности.
FРАСПОБР() - FINV() - Определяет обратное значение для F-распределения вероятности.
ФИШЕР() - FISHER() - Находит преобразование Фишера.
ФИШЕРОБР() - FISHERINV() - Находит обратное преобразование Фишера.
ПРЕДСКАЗ() - FORECAST() - Вычисляет значение линейного тренда.
ЧАСТОТА() - FREQUENCY() - Находит распределение частот в виде вертикального массива.
ФТЕСТ() - FTEST()- Определяет результат F-теста.
ГАММАРАСП() - GAMMADIST() - Находит гамма-распределение.
ГАММАОБР() - GAMMAINV() - Находит обратное гамма-распределение.
ГАММАНЛОГ() - GAMMALN() - Вычисляет натуральный логарифм гамма функции.
СРГЕОМ() - GEOMEAN() - Вычисляет среднее геометрическое.
РОСТ() - GROWTH() - Вычисляет значения в соответствии с экспоненциальным трендом.
СРГАРМ() - HARMEAN()- Вычисляет среднее гармоническое.
ГИПЕРГЕОМЕТ() - HYRGEOMDIST() - Определяет гипергеометрическое распределение.
ОТРЕЗОК() - INTERCEPT() - Находит отрезок, отсекаемый на оси линией линейной регрессии.
ЭКСЦЕСС() - KURT() - Определяет эксцесс множества данных.
НАИБОЛЬШИЙ() - LARGE() - Находит k-ое наибольшее значение из множества данных.
ЛИНЕЙН() - LINEST() - Находит параметры линейного тренда.
ЛГРФПРИБЛ() - LOGEST() - Находит параметры экспоненциального тренда.
ЛОГНОРМОБР() - LOGINV() - Находит обратное логарифмическое нормальное распределение.
ЛОГНОРМРАСП() - LOGNORMDIST() - Находит интегральное логарифмическое нормальное распределение.
МАКС() - MAX() - Определяет максимальное значение из списка аргументов.
МАКСА() - MAXA() - Определяет максимальное значение из списка аргументов, включая числа, текст и логические значения.
МЕДИАНА() - MEDIAN() - Находит медиану заданных чисел.
МИН() - MIN()- Определяет минимальное значение из списка аргументов.
МИНА() - MINA() - Определяет минимальное значение из списка аргументов, включая числа, текст и логические значения.
МОДА() - MODE() - Определяет значение моды множества данных.
ОТРБИНОМРАСП() - NEGBINOMDIST() - Находит отрицательное биномиальное распределение.
НОРМРАСП() - NORMDIST() - Выдает нормальную функцию распределения.
НОРМОБР() - NORMINV() - Выдает обратное нормальное распределение.
НОРМСТРАСП() - NORMSDIST() - Выдает стандартное нормальное интегральное распределение.
НОРМСТОБР() - NORMSINV() - Выдает обратное значение стандартного нормального распределения.
ПИРСОН() - PEARSON() - Определяет коэффициент корреляции Пирсона.
ПЕРСЕНТИЛЬ() - PERCENTILE() - Определяет k-ую персентиль для значений из интервала.
ПРОЦЕНТРАНГ() - PERCENTRANK()- Определяет процентную норму значения в множестве данных.
ПЕРЕСТ() - PERMUT()- Находит количество перестановок для заданного числа объектов.
ПУАССОН() - POISSON() - Выдает распределение Пуассона.
ВЕРОЯТНОСТЬ() - PROB() - Определяет вероятность того, что значение из диапазона находится внутри заданных пределов.
КВАРТИЛЬ() - QUARTILE() - Определяет квартиль множества данных.
РАНГ() - RANK()- Определяет ранг числа в списке чисел.
КВПИРСОН() - RSQ() - Находит квадрат коэффициента корреляции Пирсона.
СКОС() - SKEW() - Определяет асимметрию распределения.
НАКЛОН() - SLOPE() - Находит наклон линии линейной регрессии.
НАИМЕНЬШИЙ() - SMALL() - Находит k-ое наименьшее значение в множестве данных.
НОРМАЛИЗАЦИЯ() - STANDARDIZE() - Вычисляет нормализованное значение.
СТАНДОТКЛОН() - STDEV() - Оценивает стандартное отклонение по выборке.
СТАНДОТКЛОНА() - STDEVA()- Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения.
СТАНДОТКЛОНП() - STDEVP() - Определяет стандартное отклонение по генеральной совокупности.
СТАНДОТКЛОНПА() - STDEVPA()- Определяет стандартное отклонение по генеральной совокупности, включая числа, текст и логические значения.
СТОШYX() - STEYX()- Определяет стандартную ошибку предсказанных значений y для каждого значения x в регрессии.
СТЬЮДРАСП() - TDIST() - Выдает t-распределение Стьюдента.
СТЬЮДРАСПОБР() - TINV() - Выдает обратное t-распределение Стьюдента.
ТЕНДЕНЦИЯ() - TREND() - Находит значения в соответствии с линейным трендом.
УРЕЗСРЕДНЕЕ() - TRIMMEAN() - Находит среднее внутренности множества данных.
ТТЕСТ() - TTEST() - Находит вероятность, соответствующую критерию Стьюдента.
ДИСП() - VAR() - Оценивает дисперсию по выборке.
ДИСПА() - VARA() - Оценивает дисперсию по выборке, включая числа, текст и логические значения.
ДИСПР() - VARP() - Вычисляет дисперсию для генеральной совокупности.
ДИСПРА() - VARPA() - Вычисляет дисперсию для генеральной совокупности, включая числа, текст и логические значения.
ВЕЙБУЛЛ() - WEIBULL() - Выдает распределение Вейбулла.
ZТЕСТ() - ZTEST() - Выдает двустороннее P-значение z-теста.