Тема: Интерполирование функций

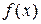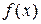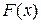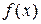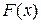Пусть функция задана таблично, либо вычисление ее требует громоздких выкладок. Заменим приближенно функцию на какую-либо функцию , так, чтобы отклонение от было в заданной области в некотором смысле минимальным. Подобная замена называется аппроксимацией функции 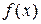, а функция 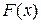– аппроксимирующей (приближающей) функцией.

Классический подход к решению задачи построения приближающей функции основывается на требование строгого совпадения значений и 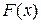в точках 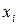( 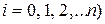, т. е.

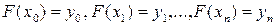. (3.1)

В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), точки 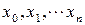– узлами интерполяции.

Часто интерполирование ведется для функций, заданных таблицами с равноотстоящими значениями аргумента . В этом случае шаг таблицы 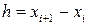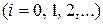является величиной постоянной. Для таких таблиц построение интерполяционных формул (как, впрочем, и вычисление по этим формулам) заметно упрощается.

Задание 1

По заданной таблице значений функции составить формулу интерполяционного многочлена Лагранжа (3.2) и построить график 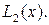Исходные данные берутся из таблицы 3.1.

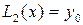
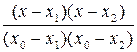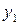
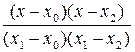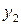
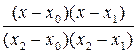+ + (3.2)

Tаблица 3.1.

№
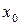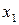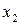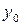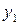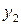				-1	-4
					-2
	-3	-1			-1
				-3	-7
	-2	-1
					-3
	-4	-2
	-1	1.5			-7
				-1	-6
	-9	-7	-4		-3
					-1
	-7	-5	-4		-4

Задание 2

Вычислить одно значение заданной функции для промежуточного значения аргумента ( 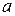) с помощью интерполяционного многочлена Лагранжа (3.3) и оценить погрешность интерполяции. Для выполнения задания исходные данные берутся из таблицы 3.2, 3.3 или 3.4.

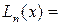
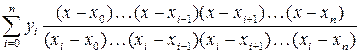(3.3)

Для погрешности 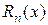выполняется неравенство

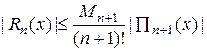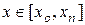, (3.4)

где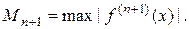

Таблица 3.2

№ варианта	Значение а	№ таблицы
	-2	3.3
	3.77	3.4
	0.55	3.3
	4.83	3.4
	3.5	3.3
	5.1	3.4
	1.75	3.3
	4.2	3.4
	-1.55	3.3
	6.76	3.4

Таблица 3.3

	-3.2	-0.8	0.4	2.8	4.0	6.4	7.6
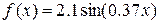	-1.94	-0.61	0.31	1.81	2.09	1.47	0.68

Таблица 3.4

	1.3	2.1	3.7	4.5	6.1	7.7	8.5
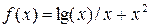	1.777	4.563	13.84	20.39	37.34	59.41	72.4

Таблица 3.5

	0.10	0.15	0.20	0.25	0.30	0.35	0.40
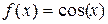	0.995	0.988	0.980	0.969	0.955	0.939	0.921

Таблица 3.6

	0.65	0.70	0.75	0.80	0.85	0.90	0.95
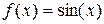	0.605	0.644	0.681	0.71	0.75	0.783	0.813

Задание 3.

Уплотнить часть таблицы заданной на отрезке 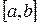функции, используя интерполяционный многочлен Ньютона (3.5) и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке 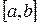с шагом 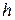. Для выполнения задания исходные данные берутся из таблиц 3.8, 3.5 и 3.6.

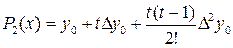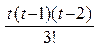
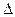+ ³y₀, (3.5)

где .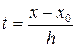

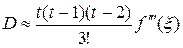, (3.6)

где 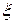– некоторая внутренняя точка наименьшего промежутка, содержащего все узлы 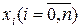и x.

Формула (3.5) называется первой интерполяционной формулой Ньютона. Если вычисляемое значение переменной ближе к концу отрезка 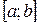, то применяют вторую формулу Ньютона – интерполирование назад (формула (3.6)).

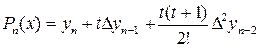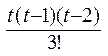
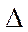+ ³y_n-3 (3.6)

где 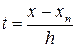и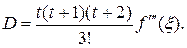

Таблица 3.7

		= -
		=
		=

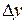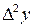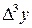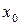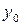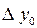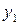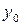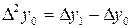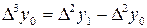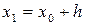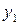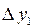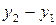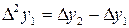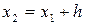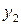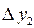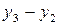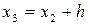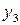Таблица 3.8

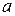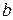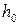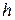№					№ таблицы
	0.65	0.80	0.05	0.01	3.6
	0.25	0.40	0.05	0.025	3.5
	0.75	0.90	0.05	0.01	3.6
	0.70	0.85	0.05	0.025	3.6
	0.80	0.95	0.05	0.025	3.6
	0.1	0.25	0.05	0.025	3.5
	0.15	0.3	0.05	0.025	3.5
	0.7	0.85	0.05	0.025	3.6
	0.2	0.35	0.05	0.01	3.5
	0.80	0.95	0.05	0.01	3.6

Примерный фрагмент выполнения работы

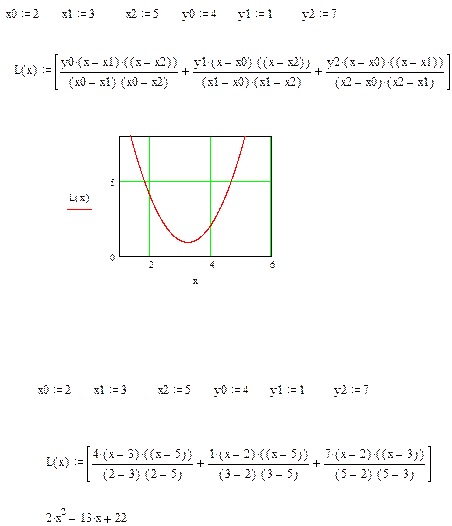
КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем особенность приближения таблично заданной функции методом интерполирования?

2. Как обосновывается существование и единственность интерполяционного многочлена?

3. Как связана степень интерполяционного многочлена с количеством узлов интерполяции?

4. Как строятся интерполяционные многочлены Лагранжа и Ньютона?

5. В чем особенности этих двух способов интерполяции?

6. Как производится оценка погрешности метода интерполяции многочленом Лагранжа?

7. Как используется метод интерполирования для уточнения таблиц функций?

8. В чем отличие между первой и второй интерполяционными формулами Ньютона?

Лабораторная работа №4