Тема: Решение уравнения c одной переменной
Рассмотрим уравнение
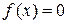(1.1)
где 
определена и непрерывна на некотором конечном или бесконечном интервале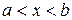 
.
Всякое значение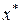 
, обращающее функцию 
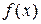в нуль, 
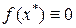, называется корнем уравнения (1.1), а способ нахождения этого значения 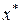и есть решение уравнения (1.1).
Найти корни уравнения вида (1.1) точно удается лишь в редких случаях. Кроме того, часто уравнение содержит коэффициенты, известные лишь приблизительно и следовательно, сама задача о точном определении корней уравнения теряет смысл. Разработаны методы численного решения уравнений вида (1.1), позволяющие отыскать приближенные значения корней этого уравнения.
При этом приходится решать две задачи:
1) отделение корней, т. е. отыскание достаточно малых областей, в каждой из которых заключен только один корень уравнения;
2) вычисление корней с заданной точностью.
Воспользуемся известным результатом математического анализа: если непрерывная функция принимает на концах некоторого интервала значения разных знаков, то интервал содержит по крайней мере один корень уравнения.
Для выделения областей, содержащих один корень, можно использовать, например, графический способом, либо двигаясь вдоль области определения с некоторым шагом, проверять на концах интервалов условие смены знака функции.
Для решения второй задачи существует многочисленные методы, из которых рассмотрим четыре: метод итераций, метод половинного деления, метод хорд, метод касательных.
Задание 1
Сделать отделение корней: графически и по программе (точность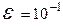 
). Индивидуальные задания приведены в таблице 1.
Задание 2
1. Провести уточнение корней методом половинного деления.
В качестве начального приближения выберем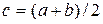 
, затем исследуем функцию на концах отрезков 
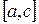и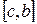 
. Выбирается тот отрезок, у которого значение функции на концах имеет противоположные знаки. Процесс продолжается до тех пор, пока не выполнится условие 
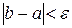. Точность 
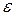принять равной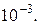 
2. Сделать уточнение корней методом простой итерации.
Пусть корни отделены и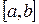 
содержит единственный корень. Уравнение (1.1) приведем к итерационному виду:
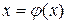(1.2)
где функция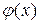 
дифференцируема на 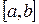и для любого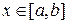 
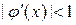. Функцию 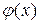можно подобрать в виде
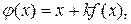(1.3)
где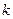 
находится из условия 
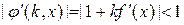, для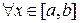 
.
Последнее условие гарантирует сходимость итерационной последовательности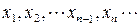 
к корню 
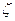. Условием окончания счета будем считать выполнение неравенства
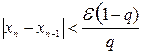
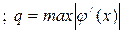(1.4)
3. Сделать уточнение корней методом хорд или касательных (X, K в таблице 1) с заданной точностью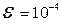 
.
Расчетная формула для метода хорд:
,
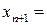
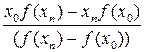для метода касательных:
,
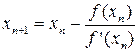Значение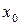 
для метода хорд и начальная точка для метода касательных выбирается из условия выполнения неравенства 
.
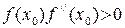В результате вычислений по этим формулам может быть получена последовательность приближенных значений корня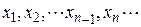 
. Процесс вычислений заканчивается при выполнении условия 
< 
( 
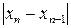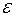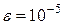). В каждом случае вывести на печать количество итераций, необходимых для достижения заданной точности.
Примерный вариант выполнения лабораторной работы на MathCad
1. Определение, построение таблиц значений и графиков функций и отделение корней уравнения y=x-sinx-0,25.
 |
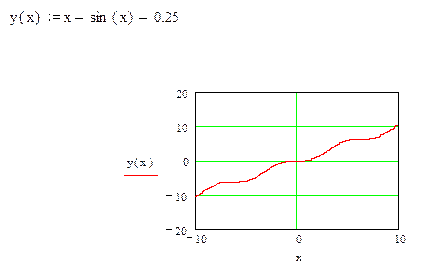Отделяем корни графически.
 |
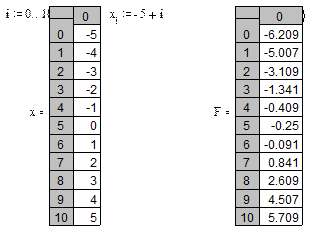Вычисляем значения аргумента и функции.
Набираем i, xi Fi. Ниже, x= и рядом щелкаем мышью, набираем F= ,также рядом щелкаем мышью.
 |
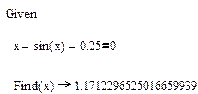2. Решение с использованием операторов given, find.
3. Символьное решение.
 |
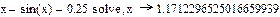4. Слева решение методом итераций, посредине методом касательных, справа методом хорд.
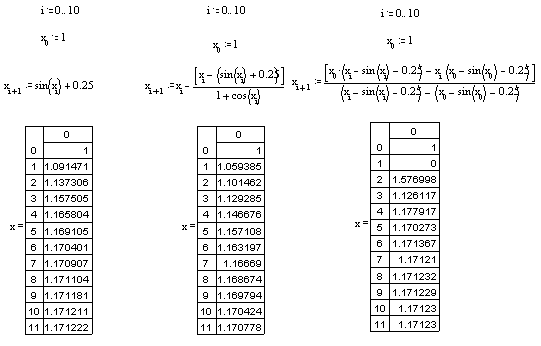
Таблица 1
| N | Метод | Уравнение |
| K |  | |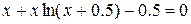
| К |  | |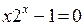
| Х |   | |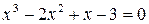
| К |  | |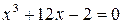
| Х |  | |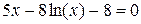
| К |  | |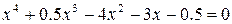
| Х |  | |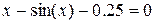
| K |  | |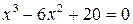
| X |  | |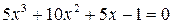
| K |  |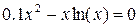
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Этапы решения уравнения с одной неизвестной.
2. Способы отделения корней.
3. Каким образом графическое отделение корней уточняется с помощью вычислений?
4. Дать словесное описание алгоритма метода половинного деления.
5. Необходимые условия сходимости метода половинного деления.
6. Условие окончания счета метода простой итерации. Погрешность метода.
7. Словесное описание алгоритма метода хорд. Графическое представление метода. Вычисление погрешности.
8. Словесное описание алгоритма метода касательных (Ньютона). Графическое представление метода. Условие выбора начальной точки.
Лабораторная работа №2