Тема: «Вычисление пределов, частных производных и дифференциалов функций нескольких действительных переменных»
Цель работы:научиться вычислять пределы, частные производные и дифференциалы функций нескольких действительных переменных.
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
- применять методы дифференциального и интегрального исчисления.
знать:
- основы дифференциального и интегрального исчисления.
Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.
Методические указания по выполнению работы:
1. Ознакомиться с теоретическим материалом по практической работе.
2. Рассмотрите образцы решения задач по теме.
3.Выполнить предложенное задание согласно варианту по списку группы.
4.Изучить условие заданий для практической работы и выполнить её.
5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
5. Оформить отчет о работе. Сделайте вывод.
Краткие теоретические и учебно-методические материалы по теме практической работы
Частные производные и полный дифференциал
Частной производной функцииz=f(x,y) по переменной х называется производная этой функции при постоянном значении переменной у; она обозначается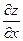 
или z'x.
Частной производной функции z=f(x, у) по переменной у называется производная по у при постоянном значении переменной х; она обозначается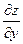 
или z'y.
Частная производная функции нескольких переменных по одной переменной определяется как производная этой функции по соответствующей переменной при условии, что остальные переменные считаются постоянными.
Полным дифференциаломфункции z=f(x, у) в некоторой точке М(х,у) называется выражение
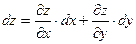(3)
Пример по выполнению практической работы
Пример 1.Найти частные производные функций:
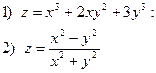
Решение: 1) Находим частную производную по переменной х при постоянном у: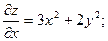 
Находим частную производную по переменной у при постоянном х: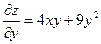 
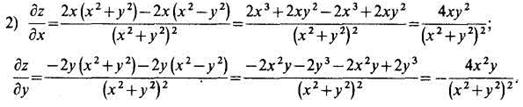
Пример 2. Вычислить значение частной производной функции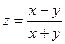 
в точке М(-2; 3).
Решение:Находим
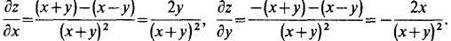
В полученные выражения подставим значения х= -2 и у = 3:
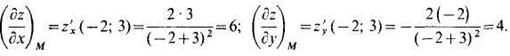
Пример 3.Вычислить полный дифференциал функции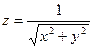 
в точке (1; -1)
Решение: Находим частные производные:
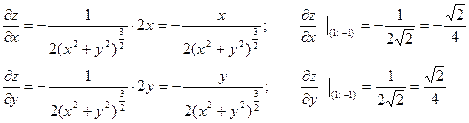
Тогда с учетом формулы (3) имеем: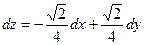 
.
Задания для практического занятия:
Вариант 1
1) Вычислить предел: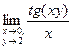 
;
2) Вычислить частные производные и полный дифференциал функции:
а)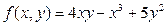 
; б)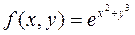 
Вариант 2
1) Вычислить предел: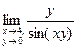 
;
2) Вычислить частные производные и полный дифференциал функции:
а)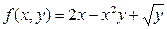 
; б)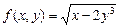 
.
Вариант 3
1) Вычислить предел: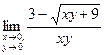 
2) Вычислить частные производные и полный дифференциал функции:
а)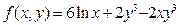 
б)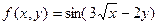 
;
Вариант 4
1) Вычислить предел: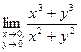 
;
2) Вычислить частные производные и полный дифференциал функции:
а)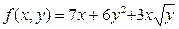 
; б)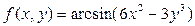 
Контрольные вопросы
1.Дать определение предела функции двух действительных переменных;
2. Какая функция двух действительных переменных называется непрерывной в точке?
3. Дать определение частных производных и полного дифференциала функции двух действительных переменных
Тема 3.5. Первообразная и интеграл.
Практическая работа № 22
«Вычисление неопределенных интегралов»
Цель работы:научиться вычислять неопределенные интегралы.
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
- применять методы дифференциального и интегрального исчисления.
знать:
- основы дифференциального и интегрального исчисления.
Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.
Методические указания по выполнению работы:
1. Ознакомиться с теоретическим материалом по практической работе.
2. Рассмотрите образцы решения задач по теме.
3.Выполнить предложенное задание согласно варианту по списку группы.
4.Изучить условие заданий для практической работы и выполнить её.
5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
5. Оформить отчет о работе. Сделайте вывод.