Для изменения указанного порядка выполнения операций используются скобки.
Алгоритм построения таблиц истинности для сложных выражений:
1. Определить количество строк:
количество строк = 2n + строка для заголовка,
n - количество простых высказываний.
2. Определить количество столбцов:
количество столбцов = количество переменных + количество логических операций;
o определить количество переменных (простых выражений);
o определить количество логических операций и последовательность их выполнения.
3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.
Пример: Составить таблицу истинности логического выражения:
D = А & (B Ú C).
Решение: Ù
1. Определить количество строк:
на входе три простых высказывания: А, В, С поэтому n=3 и количество строк = 23 +1 = 9.
2. Определить количество столбцов:
o простые выражения (переменные): А, В, С;
o промежуточные результаты (логические операции):
А - инверсия (обозначим через E);
B Ú C - операция дизъюнкции (обозначим через F);
а также искомое окончательное значение арифметического выражения:
D = А & (B Ú C). т.е. D = E & F - это операция конъюнкции.
3. Заполнить столбцы с учетом таблиц истинности логических операций.
| A | B | C | E | F | E & F |
Построение логической функции по ее таблице истинности:
Попробуем решить обратную задачу. Пусть дана таблица истинности для некоторой логической функции
Z(X,Y):
| X | Y | Z |
Составить логическую функцию для заданной таблицы истинности.
Правила построения логической функции по ее таблице истинности:
1. Выделить в таблице истинности те строки, в которых значение функции равно 1.
2. Выписать искомую формулу в виде дизъюнкции нескольких логических элементов. Число этих элементов равно числу выделенных строк.
3. Каждый логический элемент в этой дизъюнкции записать в виде конъюнкции аргументов функции.
4. Если значение какого-либо аргумента функции в соответствующей строке таблице равно 0, то этот аргумент взять с отрицанием.
Решение.
1. В первой и третьей строках таблицы истинности значение функции равно 1.
2. Так как строки две, получаем дизъюнкцию двух элементов: ( ) V ( ).
3. Каждый логический элемент в этой дизъюнкции запишим в виде конъюнкции аргументов функции X и Y: (X & Y) V (X & Y).
4. Берем аргумент с отрицанием если его значение в соответствующей строке таблицы равно 0 и получаем искомую функцию:
Z (X, Y) =( X & Y) V (X & Y).
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Пример 1.«3 – простое число» является высказыванием, поскольку оно истинно.
Не всякое предложение является логическим высказыванием.
Пример 2. Предложение «Давайте пойдем в кино» не является высказыванием.
Вопросительные и побудительные предложения высказываниями не являются.
Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Пример 3. «x+2>5» - высказывательная форма, которая при x>3 является истинной, иначе ложной.
Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Слова и словосочетания «не», «и», «или», «если..., то», «тогда и только тогда» и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Высказывания, образованные из других высказываний с помощью логических связок, называются составными(сложными). Высказывания, которые не являются составными, называются элементарными (простыми).
Истинность или ложность составных высказываний зависит от истинности или ложности элементарных высказываний, из которых они состоят.
Чтобы обращаться к логическим высказываниям, им назначают имена.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение (таблица1.1).
Таблица 1.1 - Основные логические операции
| Обозначение операции | Читается | Название операции | Альтернативные обозначения |
| НЕ | Отрицание (инверсия) | Черта сверху | |
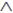 | И | Конъюнкция (логическое умножение) | ∙ & |
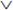 | ИЛИ | Дизъюнкция (логическое сложение) | + |
| → | Если … то | Импликация | 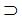 |
| ↔ | Тогда и только тогда | Эквиваленция | ~ |
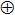 | Либо …либо | Исключающее ИЛИ (сложение по модулю 2) | XOR |
Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием (или знаком ). Высказывание А истинно, когда A ложно, и ложно, когда A истинно.
Операция, выражаемая связкой «и», называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой « • » (может также обозначаться знаками 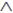 или &). Высказывание А • В истинно тогда и только тогда, когда оба высказывания А и В истинны.
или &). Высказывание А • В истинно тогда и только тогда, когда оба высказывания А и В истинны.
Операция, выражаемая связкой «или» (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio – разделение) или логическим сложением и обозначается знаком 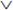 (или плюсом). Высказывание А
(или плюсом). Высказывание А 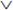 В ложно тогда и только тогда, когда оба высказывания А и В ложны.
В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Операция, выражаемая связками «если …, то», «из … следует», «... влечет …», называется импликацией(лат. implico – тесно связаны) и обозначается знаком → . Высказывание А→В ложно тогда и только тогда, когда А истинно, а В ложно.
Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «... равносильно …», называется эквиваленцией или двойной импликацией и обозначается знаком ↔ или ~ . Высказывание А↔В истинно тогда и только тогда, когда значения А и В совпадают.
Операция, выражаемая связками «Либо … либо», называется исключающее ИЛИ или сложением по модулю 2 и обозначается XOR или 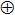 . Высказывание А
. Высказывание А 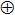 В истинно тогда и только тогда, когда значения А и В не совпадают.
В истинно тогда и только тогда, когда значения А и В не совпадают.
Импликацию можно выразить через дизъюнкцию и отрицание: 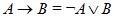 .
.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию: 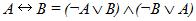 .
.
Исключающее ИЛИ можно выразить через отрицание, дизъюнкцию и конъюнкцию: 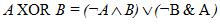 .
.
Операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Приоритет выполнения: отрицание, конъюнкция, дизъюнкция, исключающее или, импликация и эквиваленция.
Логическая формула - это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).
Логическая функция - это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.
Пример 4. 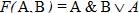 – логическая функция двух переменных A и B.
– логическая функция двух переменных A и B.
Значения логической функции для разных сочетаний значений входных переменных – или, как это иначе называют, наборов входных переменных – обычно задаются специальной таблицей. Такая таблица называется таблицей истинности.
Приведем таблицу истинности основных логических операций (таблица 1.2)
Таблица 1.2
| A | B | 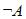 | 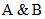 | 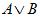 | 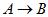 | 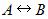 | 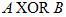 |
Пример 5. Составить таблицу истинности для формулы И–НЕ, которую можно записать так: 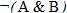 .
.
1. Определить количество строк:
На входе два простых высказывания: А и В, поэтому n=2 и количество строк =22+1=5.
2. Определить количество столбцов:
Выражение состоит из двух простых выражений (A и B) и двух логических операций (1 инверсия, 1 конъюнкция), т.е. количество столбцов таблицы истинности = 4.
3. Заполнить столбцы с учетом таблиц истинности логических операций (таблица 1.3).
Таблица 1.3. Таблица истинности для логической операции
| A | B | 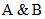 | 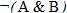 |
Логические формулы можно также представлять с помощью языка логических схем.
Существует три базовых логических элемента, которые реализуют три основные логические операции :
- логический элемент «И» – логическое умножение – конъюнктор;
- логический элемент «ИЛИ» – логическое сложение – дизъюнктор;
- логический элемент «НЕ» – инверсию – инвертор.
