Расстояние от точки до прямой.

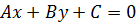Рассмотрим прямую , заданную уравнением , и точку с координатами .

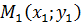Если точка 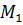принадлежит прямой, то её координаты удовлетворяют уравнению этой прямой, то есть 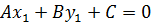– истинное равенство.

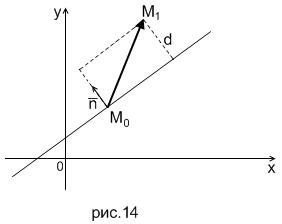
Пусть точка 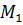не лежит на прямой , то есть 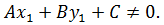Найдём расстояние от неё до этой прямой.

Из рис. 14 очевидно, что искомое расстояние равно .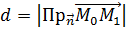

Вычислив проекцию вектора 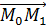на направление нормального вектора прямой 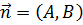, получим следующую формулу:

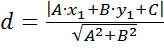. (20)

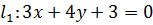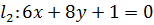Пример 14. Выясним, являются ли прямые и параллельными, и если являются, то вычислим расстояние между ними.

Решение. Из сравнения уравнений данных прямых с общим уравнением прямой (см. (4)) имеем 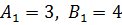, 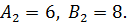Проверим, выполняется ли условие параллельности этих прямых (см.(11)).

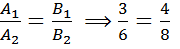– условие выполняется, прямые параллельны. Так как имеет место формула для вычисления расстояния от точки до прямой (см.(20)), возьмём на одной прямой любую точку 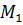и вычислим расстояние от неё до другой прямой. Найденное таким образом расстояние будет равно искомому расстоянию между данными прямыми.

На прямой с уравнением 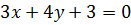выберем точку с координатой 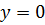, тогда её координата 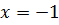. Выбранная точка 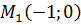принадлежит прямой . Вычислим расстояние от неё до прямой (см.(20)).

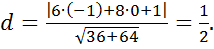
Ответ: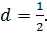

Пример 15. Составим уравнение биссектрисы угла 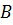треугольника, вершины которого расположены в точках .

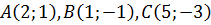Решение. Биссектриса угла 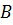обладает тем свойством, что все её точки равноудалены от сторон треугольника 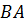и 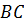. Составим уравнения сторон 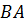и , и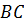спользуя, например, каноническое уравнение (см. (14)).

Направляющим вектором прямой 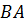является 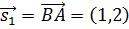и уравнение этой прямой, проходящей через точку 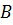, имеет вид 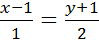. Или в общем виде .

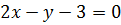Направляющим вектором прямой 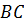является 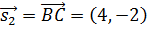и уравнение этой прямой, проходящей через точку 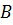, имеет вид 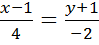. Или в общем виде .

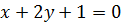Любая точка искомой биссектрисы имеет координаты 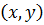. Расстояния от неё до прямых 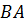и 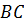, которые равны между собой, вычислим по формуле (20) и получим уравнение, связывающее координаты всех точек биссектрисы, то есть её уравнение.

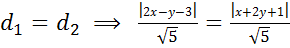или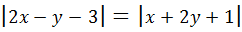

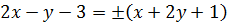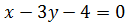
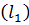Получаем два результата: или

и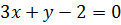

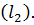
Биссектрисой 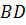треугольника 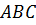является одна из этих прямых.

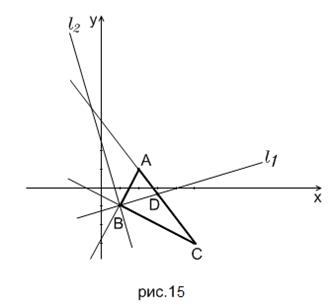
Рассмотрим рис. 15. Видим, что искомая прямая должна пересекать сторону треугольника 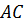в точке 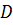, которая принадлежит отрезку 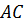. Составим уравнение стороны 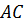и найдём точку её пересечения с первой из найденных прямых. Направляющим вектором прямой 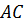является 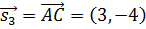и уравнение этой прямой, проходящей через точку 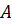, имеет вид 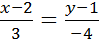. Или в общем виде .

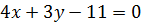Координаты точки пересечения 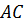и являются решением системы уравнений

,

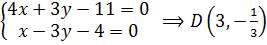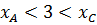
Получили координаты точки 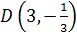и убедились в том, что её абсцисса 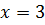принадлежит интервалу 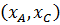, то есть найденная точка принадлежит стороне треугольника 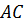(см. рис. 12).Следовательно, искомым является уравнение прямой .

Ответ: .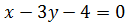

Пучок прямых.

Определение. Пучком прямых называется множество прямых, проходящих через одну общую точку.

Точку можно задать как пересечение двух непараллельных прямых. Теорема. Прямая принадлежит пучку прямых, проходящих через точку, являющуюся точкой пересечения прямых и , тогда и только тогда, когда координаты любой её точки удовлетворяют уравнению

, где (21).

Это уравнение называется уравнением пучка прямых на плоскости.

Пример 16. Составим уравнение прямой, проходящей через точку и точку пересечения прямых и .

Решение. Используем тот факт, что через точку пересечения двух заданных прямых проходит и искомая прямая . То есть эти три прямые принадлежат одному пучку прямых. Следовательно, уравнение прямой можно искать из уравнения пучка (см. (21)): .

Если , то можно обозначить и тогда уравнение имеет вид . Так как точка принадлежит искомой прямой , её координаты удовлетворяют уравнению этой прямой, то есть выполняется равенство , из которого получаем . Подставляем найденное значение в уравнение прямой и после преобразования получаем уравнение искомой прямой: .

Ответ.

Пример 17. Составим уравнение прямой, проходящей через точку пересечения прямых и параллельно прямой .

Решение. Искомая прямая принадлежит пучку прямых, проходящих через точку пересечения двух прямых и , заданных в условии своими уравнениями. Поэтому её уравнение можно найти из уравнения пучка (см.(21)).

Преобразуем это уравнение в общее уравнение прямой (см. (4)).

Имеем ,

Искомая прямая параллельна по условию прямой . Из условия параллельности (см. (11)) следует, что . Отсюда получаем, что . Примем, например, и . При таком выборе уравнение искомой прямой примет вид . После упрощения получаем уравнение

Ответ:

Задачи для самостоятельной работы.

1.Какой угол составляют данные прямые с осью ОХ?

а) ;

б) . (см.(1),(2))

Ответ: а) ; б) .

2.Вычислите угол между прямыми и :

а) и

б) и . (см.(6),(7))

Ответ: а) ; б) .

3. Выясните, являются ли данные прямые параллельными:

а) и ;

б) и ;

в) и . (см.(10),(11))

Ответ: а) нет; б) да; в) да.

4. Выясните, являются ли данные прямые взаимно перпендикулярными:

а) и ;

б) и ;

в) и . (см. (8),(9))

Ответ: а) нет; б) да; в) да.

5. Составьте общее уравнение прямой, проходящей через точку и имеющей угловой коэффициент 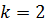. (см.(2),(4))

Ответ:

6. Найдите угол наклона прямой . (см. (2),(1))

Ответ: .

7. Составьте уравнение прямой, проходящей через точку параллельно прямой , используя уравнение с угловым коэффициентом. (см.(10), (2))

Ответ: .

8. Составьте уравнение прямой, проходящей через точку параллельно прямой , используя общее уравнение прямой. (см. (11), (4), (17))

Ответ:

9. Составьте уравнение прямой с угловым коэффициентом, если известно, что она проходит через точку перпендикулярно прямой . (см.(8), (2))

Ответ:

10. Составьте общее уравнение прямой, проходящей через точку перпендикулярно прямой (см. (9), (4), или(18))

Ответ:

11. Убедитесь в том, что прямые и параллельны, и вычислите расстояние между ними. (см. (11), (19))

Ответ:

12. Составьте общее уравнение прямой, проходящей через точку пересечения прямых и параллельно прямой . Составьте общее уравнение прямой, проходящей через ту же точку перпендикулярно прямой

(см. (9),(11), (4) или (21))

Ответ: , .

13. Составьте общее уравнение прямой, проходящей через точки и (см. (16), (4))

Ответ:

14. Составьте уравнения прямых, на которых лежат стороны четырёхугольника с вершинами в точках . (см.(16))

Ответ:

15. Точки являются вершинами треугольника. Вычислите длину его высоты, проведенной из вершины 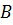, составьте уравнения прямых, на которых лежат высота и медиана, проведенные из этой же вершины. (см.(20),(18),(16))

Ответ: , ,

.

16. Найдите проекцию точки на прямую (см. пример 12 )

Ответ: .

17. Составьте уравнения прямых, делящих пополам углы между прямыми и . (см.(20))

Ответ: и .

18. Точки являются вершинами треугольника. Составьте уравнение биссектрисы угла 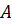. (см.(20))

Ответ:

19. Составьте общее уравнение прямой, проходящей через точку и точку пересечения прямых

и (см.(21))

Ответ:

20. Дано общее уравнение прямой . Составьте её уравнение в отрезках и найдите точки её пересечения с осями координат.

Ответ:

21. Даны две смежные вершины параллелограмма , и

точка пересечения его диагоналей . Составьте уравнения

сторон и диагоналей этого параллелограмма.

Ответ: CD

BD .

22. Даны точки и . Отрезок 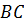является основанием равнобедренного треугольника 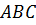. Точка - точка пересечения его медиан. Найдите координаты вершины этого треугольника и запишите уравнения его сторон.

Ответ: ,

,

,

Оглавление.

1. Уравнение прямой с угловым коэффициентом. Стр. 4

2. Общее уравнение прямой. Стр. 8

3. Взаимное расположение прямых на плоскости. Стр. 10

4. Другие виды уравнений прямой на плоскости. Стр. 15

5. Расстояние от точки до прямой. Стр.24

6. Пучок прямых. Стр. 28

7. Список литературы. Стр.35

Список литературы.

1. Канатников А.Н., Крищенко А.П. Аналитическая геометрия. М.: Издательство МГТУ им. Н.Э.Баумана, 2005. 374 с.

2. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М.: Наука, 1965. 432 с.