И.В. Дубограй, О.В. Скуднева, В.Ю. Чуев.
И.В. Дубограй, О.В. Скуднева, В.Ю. Чуев.
ПРЯМАЯ НА ПЛОСКОСТИ
Электронное учебное издание
Методические указания к решению задач
по теме
Москва
УДК №3.11/12, №4.11/12
Рецензент: доц., к.ф.-м.н., Леонид Дмитриевич Покровский
Дубограй И.В., Скуднева О.В., Чуев В.Ю..
Прямая на плоскости: электронное учебное издание. - М.: МГТУ имени Н.Э. Баумана, 2014. 35 с.
Издание содержит основные понятия и определения по теме "Прямая на плоскости», предусмотренные учебным планом МГТУ им. Н.Э.Баумана. Представлен справочный материал, содержащий основные определения, формулировки необходимых теорем. Даны подробные решения задач со ссылками на необходимые формулы.
Для студентов МГТУ имени Н.Э. Баумана всех специальностей.
Электронное учебное издание
Дубограй Ирина Валерьевна
Скуднева Оксана Валентиновна.
Чуев Василий Юрьевич
Прямая на плоскости
© 2014 МГТУ имени Н.Э. Баумана
Введение
В данном пособии представлен справочный теоретический материал, необходимый для освоения одного из важных разделов аналитической геометрии. В сжатой форме изложены все необходимые сведения из теории, подробно разобраны решения типовых задач.
Разделы «указаний» полностью соответствуют программе обучения студентов, утверждённой методической комиссией МГТУ им. Н.Э. Баумана.
Авторы преследовали цель активизировать самостоятельную работу студентов, улучшить качество подготовки учащихся по данному разделу математики.
Методические указания предназначены для студентов первого курса всех специальностей, а также будут полезны студентам старших курсов в качестве справочного материала.
Общее уравнение прямой.
Отметим, что уравнения прямой вида (2) и (3), рассмотренные ранее, являются линейными. Имеет место следующая теорема.
Теорема. Множество точек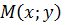 
плоскости принадлежит прямой 
тогда и только тогда, когда их координаты удовлетворяют линейному уравнению, а именно, уравнению вида
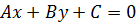, где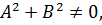 
(4) то есть 
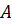и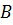 
одновременно не равны нулю.
Уравнение вида (4) называется общим уравнением прямой на плоскости.
Все рассмотренные уравнения прямой связаны между собой. Так, например, пр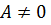и 
и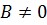 
уравнение (4) приводится к уравнению с угловым коэффициентом вида (2): 
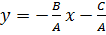, где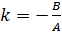 
.
При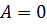 
, 
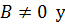равнение (4) после преобразования приводится к уравнению вида 
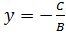с угловым коэффициентом 
.
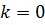При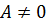 
, 
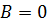получаем из (4) уравнение 
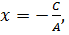что соответствует уравнению вида (3).
Обратно, если уравнение с угловым коэффициентом вида (2) переписать в виде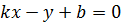 
, то оно будет соответствовать общему уравнению вида (4).
Пример 3. Выясним, под каким углом прямая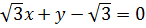 
пересекает ось 
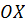, и найдем точки ее пересечения с осями координат.
Решение. Приведем уравнение заданной прямой к виду (2), то есть запишем её уравнение с угловым коэффициентом. Выразив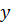 
из исходного уравнения этой прямой, получим уравнение 
.
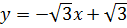Отсюда следует, что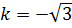 
и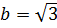 
. Следовательно, искомый угол 
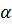таков, что 
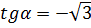(см.(1)), т. е. 
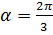- угол, под которым данная прямая пересекает ось .
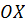Ось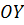 
пересекается прямой в точке 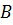с ординатой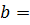 
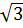, т. е. в точке 
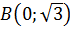. (см. рис.2)
Чтобы найти точку 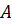, в которой прямая пересекает ось 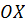, учтем, что в этой точке координата 
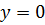, и подставив в уравнение заданной прямой
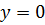, получим 
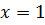. Т.е. координаты точки 
.
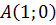Ответ.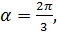 
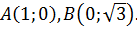
Векторное уравнение прямой.
Если зафиксированная точка 
и произвольная точка 
прямой заданы своими радиус-векторами (см. рис. 9)
и 
, то 
или 
.
Отсюда следует, что для радиус-вектора любой точки прямой имеет место уравнение
. (15)
Это уравнение называется векторным уравнением прямой 
Пучок прямых.
Определение. Пучком прямых называется множество прямых, проходящих через одну общую точку.
Точку можно задать как пересечение двух непараллельных прямых. Теорема. Прямая принадлежит пучку прямых, проходящих через точку, являющуюся точкой пересечения прямых 
и 
, тогда и только тогда, когда координаты любой её точки 
удовлетворяют уравнению
, где 
(21).
Это уравнение называется уравнением пучка прямых на плоскости.
Пример 16. Составим уравнение прямой, проходящей через точку 
и точку пересечения прямых 
и 
.
Решение. Используем тот факт, что через точку пересечения двух заданных прямых проходит и искомая прямая . То есть эти три прямые принадлежат одному пучку прямых. Следовательно, уравнение прямой можно искать из уравнения пучка (см. (21)): 
.
Если 
, то можно обозначить 
и тогда уравнение имеет вид 
. Так как точка принадлежит искомой прямой , её координаты удовлетворяют уравнению этой прямой, то есть выполняется равенство 
, из которого получаем 
. Подставляем найденное значение 
в уравнение прямой и после преобразования получаем уравнение искомой прямой: 
.
Ответ. 
Пример 17. Составим уравнение прямой, проходящей через точку пересечения прямых 
и 
параллельно прямой 
.
Решение. Искомая прямая принадлежит пучку прямых, проходящих через точку пересечения двух прямых 
и 
, заданных в условии своими уравнениями. Поэтому её уравнение можно найти из уравнения пучка (см.(21)). 
Преобразуем это уравнение в общее уравнение прямой (см. (4)).
Имеем 
, 
Искомая прямая параллельна по условию прямой . Из условия параллельности (см. (11)) следует, что 
. Отсюда получаем, что 
. Примем, например, 
и 
. При таком выборе уравнение искомой прямой примет вид 
. После упрощения получаем уравнение 
Ответ:
Задачи для самостоятельной работы.
1.Какой угол составляют данные прямые с осью ОХ?
а) 
;
б) 
. (см.(1),(2))
Ответ: а) 
; б) 
.
2.Вычислите угол между прямыми и :
а) 
и 
б) 
и 
. (см.(6),(7))
Ответ: а) 
; б) 
.
3. Выясните, являются ли данные прямые параллельными:
а) 
и 
;
б) 
и 
;
в) 
и 
. (см.(10),(11))
Ответ: а) нет; б) да; в) да.
4. Выясните, являются ли данные прямые взаимно перпендикулярными:
а) 
и 
;
б) 
и 
;
в) 
и 
. (см. (8),(9))
Ответ: а) нет; б) да; в) да.
5. Составьте общее уравнение прямой, проходящей через точку 
и имеющей угловой коэффициент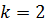 
. (см.(2),(4))
Ответ: 
6. Найдите угол наклона прямой 
. (см. (2),(1))
Ответ: 
.
7. Составьте уравнение прямой, проходящей через точку 
параллельно прямой 
, используя уравнение с угловым коэффициентом. (см.(10), (2))
Ответ: 
.
8. Составьте уравнение прямой, проходящей через точку параллельно прямой 
, используя общее уравнение прямой. (см. (11), (4), (17))
Ответ: 
9. Составьте уравнение прямой с угловым коэффициентом, если известно, что она проходит через точку 
перпендикулярно прямой 
. (см.(8), (2))
Ответ: 
10. Составьте общее уравнение прямой, проходящей через точку 
перпендикулярно прямой 
(см. (9), (4), или(18))
Ответ: 
11. Убедитесь в том, что прямые 
и 
параллельны, и вычислите расстояние между ними. (см. (11), (19))
Ответ: 
12. Составьте общее уравнение прямой, проходящей через точку пересечения прямых 
и 
параллельно прямой 
. Составьте общее уравнение прямой, проходящей через ту же точку перпендикулярно прямой 
(см. (9),(11), (4) или (21))
Ответ: 
, 
.
13. Составьте общее уравнение прямой, проходящей через точки 
и 
(см. (16), (4))
Ответ: 
14. Составьте уравнения прямых, на которых лежат стороны четырёхугольника с вершинами в точках 
. (см.(16))
Ответ: 
15. Точки 
являются вершинами треугольника. Вычислите длину его высоты, проведенной из вершины 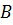, составьте уравнения прямых, на которых лежат высота и медиана, проведенные из этой же вершины. (см.(20),(18),(16))
Ответ: 
, 
,
.
16. Найдите проекцию точки 
на прямую 
(см. пример 12 )
Ответ: 
.
17. Составьте уравнения прямых, делящих пополам углы между прямыми 
и 
. (см.(20))
Ответ: 
и 
.
18. Точки 
являются вершинами треугольника. Составьте уравнение биссектрисы угла 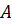. (см.(20))
Ответ: 
19. Составьте общее уравнение прямой, проходящей через точку 
и точку пересечения прямых
и 
(см.(21))
Ответ: 
20. Дано общее уравнение прямой 
. Составьте её уравнение в отрезках и найдите точки её пересечения с осями координат.
Ответ: 
21. Даны две смежные вершины параллелограмма 
, 
и
точка пересечения его диагоналей 
. Составьте уравнения
сторон и диагоналей этого параллелограмма.
Ответ: 
CD 
BD 
.
22. Даны точки 
и 
. Отрезок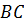 
является основанием равнобедренного треугольника 
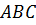. Точка 
- точка пересечения его медиан. Найдите координаты вершины этого треугольника и запишите уравнения его сторон.
Ответ: 
,
,
,
Оглавление.
1. Уравнение прямой с угловым коэффициентом. Стр. 4
2. Общее уравнение прямой. Стр. 8
3. Взаимное расположение прямых на плоскости. Стр. 10
4. Другие виды уравнений прямой на плоскости. Стр. 15
5. Расстояние от точки до прямой. Стр.24
6. Пучок прямых. Стр. 28
7. Список литературы. Стр.35
Список литературы.
1. Канатников А.Н., Крищенко А.П. Аналитическая геометрия. М.: Издательство МГТУ им. Н.Э.Баумана, 2005. 374 с.
2. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М.: Наука, 1965. 432 с.
И.В. Дубограй, О.В. Скуднева, В.Ю. Чуев.
ПРЯМАЯ НА ПЛОСКОСТИ
Электронное учебное издание
Методические указания к решению задач
по теме
Москва
УДК №3.11/12, №4.11/12
Рецензент: доц., к.ф.-м.н., Леонид Дмитриевич Покровский