Арифметические и логические операторы

+- сложение(А+В), слагаемые должны быть одинакового размера. Если одно из слагаемых скаляр он добавляется ко всем элементам другого операнда

- -вычитание(А-В), уменьшаемое и вычитаемое должны быть одинакового размера, за исключен

нием когда один из вычитаемых скаляр. Скаляр вычитается из всех элементов другого операнда

.+- умножение(А*В), поэлементное перемножение 2х массивов одинакового размера. На скаляр умножаем все элементы массива.

\- решение систем линейных уравнений(АХ=В). Если А- квадратная матрица размером nхn уравнение решается методом исключения Гаусса. Если А- прямоугольная матрица размером mxn, а В- матрица размером nxk система решается на основе минимизации 2-й нормы невязок.

.\- левое деление массивов (А.\В), результатом является матрица. С элементами B(i,j)/A(i,j);матрицы должны быть одинаковых размеров.
/- (XA=B) решение системы линейных уравнений.
./(А./B) правое деление массивов. Результатом является матрица с элементами А(i,j)/A(i,j). Матрицы должны быть одинаковых размеров.

^- степень матрицы(А^p). P- целое положительное число, если p-целое отрицательное число, то степень матрицы вычисляется путем перемножения на обратную матрицу
.^- степень массива(А.^В).Результатом является матрица с элементами А(i,j)^B(i,j).Матрицы должны быть одинаковых размеров
‘-транспонирование матрицы. Для действительных результатов является транспонированная матрица
.’- транспонирование массива.

Логические операторы. Операции соотношения.
Операции соотношения выполняют поэлементное сравнение2-х массивов, в результате возвращают массив того же размера, элементы которого равны единицы, если они совпадают; в противном случае = 0.
(<,=<,>,>=,==,~=) синтаксис: A<B A>B A=<B A>=B A==B A~=B
< =< > =>- используются для сравнения действительной части чисел
== ~- сравнивают и действительные и мнимые числа.

Логические операции
& ~ | синтаксис:
A&B A|B ~A
Эти логические операции соответствует элементам булевой алгебры
AND NOT OR

& ~ |
Массив рассматривается как совокупность булевых переменных поэтому значение 0 соответствует значению FALSE. Любое другое значение соответствует булевым значениям TRUE. Логические операции имеют более низкий приоритет по отношению к арифметическим операциям.

Специальные символы, переменные и константы.
Формирование векторов и матриц.
[]- указывают последовательность выходных параметров при обращении к функциям возвращающим более одного параметра.

()- а) указывает порядок выполнения операции в арифметических выражениях б) указывает индексы элемента матрицы, вектора или массива в) указывает последовательность входных параметров функций.

=- знак присваивания в арифметических выражениях.

.- а) является десятичной точкой б) используется для поэлементного выполнения операций на массивах данных.
,- используется а) для указания индексов элемента вектора, матрицы, массива б) для отделения операторов языка MATLAB
;- разделитель, используется: а) для отделения строк матрицы или массивов б) для подавления вывода на экран результата вычислений.
:- используется а) в заголовке цикла FOR б) для формирования векторов, выделения строк, столбцов подблоков массива.
%- является указателем а) логического указателя строки, т.е. текст следующий за этим символом игнорируется б) указывает на строки комментария.

!- является указателем ввода команды DOC
Ans результат выполнения последней операции

Iили I- мнимая единица, константа и j первоначально присваивается значение равное (sqrt-1)=sqrt(-1). Они используются для ввода комплексных чисел.

Pi-число p:П=3,14.
Математические функции
В системе MATLAB имеется библиотека математических функций. В каждой функции соответствует определенное имя. Функция ставит в соответствии от значения своих аргументов, значение результата. Аргументы функций указываются в круглых скобках после имени функции, если их больше одной разделяются запятыми. В качестве аргумента можно использовать другие функции и любые выражения языка MATLAB.
Элементарные функции

Это обычно функции от одной переменной. Имя переменной к которой присваивается значение функции располагается слева от знака равенства, если значения переменной( присваиваемой) не указывается значения функции присваивается служебной переменной ans. Тип результата вычисления математической функции совпадает с типом ее аргумента.

Abs.синтаксис: у= abs(x)-абсолютное значение. Для массива действительных чисел функция у=abs(x)возвращает массив у абсолютных значений элементов х. Для строковой переменной S(y= abs(s)) функцияy=abs(x) возвращает вместо символов, включая пробелы их ABSCII-коды.
ANGLE- аргументы комплексного числа. Синтаксис: P= angle(z) Для массива комплексных чисел z эта функция возвращает массив значений аргумента для элементов z.
Для вычисления аргумента комплексного числа используется следующее соотношение:

angle(z)= atan 2 (imag(z), real(z)).

REAL- синтаксис x= real(z), IMAG синтаксис x= imag(z)- действительная и мнима части комплексного числа. Для массивов комплексных чисел z функция x=reab(z) Возвращает массив действительных

чисел, а x=imag(z) массив мнимых частей элементов z.
SIGN- симметричен s=sign(z) вычесление знака числа. Для массива действительных чисел х эта функция возвращает массив s тех же размеров на месте положительного числа --1, на месте нулевого- 0. Для массива комплексных чисел zэта функция возвращает массив комплексных чисел:

S=Z ./abs(z), модуль который равен 1
1. ceil y= ceil(x)
2. FIX y=fix(x) - функции округления
3. FLOOK y=flook(x)
4. ROUND y=round(x)
1.- возвращает значение округленные до ближайшего целого > или равного x(>=).

2.-возвращает значения с усечением дробной части числа.
3.- возвращает значение округленные до ближайшего целого =< x.
4.- возвращает значение округленные до ближайшего целого.
Для массива комплексных чисел z эти функции применяются одновременно к действительной и мнимой частям.
REM: четная (х, у)- функция остатка. Для действительных х и у это функция вычисляет остаток от деления х и у.Для массивов чисел эта функция применяется поэлементно.

GCD: g= gcd (m, n) наибольший больший делитель [g,c,d]= gcd(m, n) эта функция вычисляет наиболее общий делитель 2х целых чисел mи n кроме наибольшего общего делителя вычисляет 2 множителя c и d таких, что выполняет соотношение g= m* c+ n* d.
Для массива чисел эту функцию не применяют.
LCM: наименьшее общее кратное. Синтаксис: y= lcm(m, n). Эта функция вычисляет наименьшее общее кратное 2х целых чисел m и n. Для массивов не применяется.
EXP (экспонента).

Тригонометрические функции

SIN, SIN H-функции синуса.

1) V= sin(z)
2) V=sinh(z)
1. вычисляет sin значений элементов массива z.

2. вычисляет гиперболический sin от значений элементов массива z углы измеряются в радианах.
1). V= asin(z)
2). V= asinh(z)
1. вычисляет обратную функцию sin от значений элементов массива z.
2.вычисляет обратную функцию гиперболического sin от значений элементов массива z углы измеряются в радианах.

CSC, CSCH-функции косеканса.
1). V=csc(z)
2). V=csch(z)
1. вычисляет косеканс от значений элементов массива z.
2. вычисляет гиперболический косеканс от значений элемента массива z.
COS, COSH- функции косинуса.
1) V= cos(z)
2) V= cosh(z)

1.вычисляет cos от значений элементов массива z.
2. вычисляет гиперболический cos от значений элементов массива z.
TAN, TANH- функции тангенса.

1) V= tan(z)
2) V=tanh)(z)
1. выселяет тангенс от значений элементов массива z.

2. вычисляет гиперболический тангенс от значений элементов массива z.

Матричные функции
Характеристика матриц
NORM- нормы векторов и матриц. Синтаксис: 1. n=norm(v,p)- вычисляет p- нормы вектора V.
RANK- матрицы p r=rank(A) эта функция возвращает rank- матрицы.
DET- определитель матрицы d=det(A)- эта функция вычисляет определитель квадратной матрицы; если матрица целочисленная, то результатом является целое число.
TRIU-формирование верхней матрицы (массива).
1) u=triu (x)
2) u=triu (x, k)
1)-сохраняет часть матрицы (массива) Х.
2)-сохраняет часть матрицы (массива) Х начиная с диагонали с № К
при К>0 это № К-ой верхней диагонали.
при К<0 это № К-ой нижней диагонали

FLIRLR-поворот матрицы относительно вертикальной оси.
B=flipir (A)
Это функция переставляет столбцы матрицы А симметрично относительно вертикальной оси. Если матрица А имеет нечетное число столбцов, то средний столбец остается на своем месте.

FLIPUD-поворот матрицы относительно горизонтальной оси.
B=flipud (A)
Это функция переставляет строки матрицы А симметрично относительно горизонтальной оси. Если матрица А имеет нечетное число строк, то средняя строка остается на своем месте

ROT 90-поворот матрицы на 90 градусов.

1. B=rot 90(A)

2. B=rot 90(A,K)

3. -осуществляет поворот матрицы А размером M*N на 90 градусов против часовой стрелки.

-это функция поворачивает матрицу А размером M*N yf 90 градусов против часовой стрелки 90*, К=+_1;+_2

Операции над матрицами.

DIAG-формирование или извлечение диагоналей матрицы.

x=diag (v)

x=diag (v, k)

v=diag (x)

v=diag (x, k)

1. формирует квадратную матрицу Х с вектором v на главной диагонали.

2. Формирует матрицу Х с вектором u на К-ой диагонали.

3. Извлекает из матрицы Х главную диагональ.

4. Извлекает из матрицы Х квадратную диагональ
при К>0, это номер К-ой верхней диагонали
при К<0, это номер К-ой нижней диагонали .

TRIL-формирование нижней матрицы.

L=tril (x)

L=tril (x, k)
-

1.сохраняет нижнюю часть матрицы Х

2.сохраняет нижнюю часть матрицы Х начиная с диагонали с № К
при К>0, № К-ой верхней диагонали,
при К<0, № К-ой нижней диагонали.

Решение систем линейных уравнений
\, /- решатели систем линейных уравнений
Синтаксис: x=B\A- эта функция находит решение системы уравнений вида AX=B, где а- прямоугольная матрица размера nxn.

Графические команды и функции
Элементы графической функции системы MATLAB позволяют построить на экране и вывести на печатающее устройство следующие типы графиков:

1. Линейный
2. Логарифмический
3. Полулогарифмический
4. Полярный

Для каждого графика можно задать заголовок нанести обозначение осей, а также масштабную сетку.

Двумерные графики
1. PLOT- график в линейном масштабе. Синтаксис:
1 plot(y)
2 plot(x;y)
3 plot(x,y,s)
4 plot(x,y,s,x2,y2,s2,...)
1. строит график элементов одномерного массива у в зависимости от номера элемента.
2. соответствует построению обычной функции если одномерный массив х соответствует значениям аргумента, одномерный массив у значениям функции.
3. позволяет выделить график функции указов способ отображения линии, способ отображения точек, цвет линий и точек с помощью строковой переменной S, которая может включать до 3х символов из:

Тип линии:

- непрерывная - - штриховая : двойной пунктир -. штрих пунктирная

Тип точки:

.точка + плюс *звездочка окружок хкрестик

Цвет

y желтый m фиолетовый cголубой rкрасный g зеленый b синий wбелый kчерный

4. позволяет обьеденить на одном графике несколько функций y1(x1), y2(x2)...
Определив для каждой из них свой способ отаброжения.
2. LOGLOG- график в логшарифмическом маштабе.
Синтаксис: 1. loglog (x, y)
2. loglog (x, y, s)
3. loglog (x, y, s, x1,y1, s1...)
Эти комманды анологичны функциям PLOT но используют по обеим осям логорифмический маштаб вместо линейного.
3. SEMILOGX- Синтаксис (график в полулогорифмическом маштабе):
semilogx(x, y)
semilogx(x, y, s)
semilogx(x, y, s, x2, y2, s2...)
4. SEMILOGY semilogy(x, y)
semilogy(x, y, s)
semilogy(x, y, s, x1, y2, s2...)
semilogx- использует логарифмический маштаб по оси х и линейный маштаб по оси у.
semilogy- использует логарифмический маштаб по оси у и линейный маштаб по оси х
5. POLAR- график в полярных координатах:
polar(phi, rho)
polar(phi, rho, s)
Эти комманды реализуют построение графиков в полярных координатах задаваемых углом phi и радиусом rho.

под блоков массива.

% является указателем а) логич. конца строки, т.е. текст следуюший за этим символом игнорируется б) указывает на строки комментария.

! является указателем ввода комманды dos

Ans результат выполнений последней операции.

I или - мнимая единица , константа и j первоначально присвоив. значение равное

( )=sqrt (-1). Они использ. для ввода компл. чисел.

Pi- число p:п=3.14

МАТЕМАТИЧЕСКИЕ ФУНКЦИИ.

В ик-ме MATLAB имеется библиотека математ.фун-й. В каждой фун-ции соответ-ет определ-е имя.Фун-я ставит в соответствие от значения своих аргументов, значение результата. А ргументы функций указываются в круг. скобках после имени функции, если их больше одной разделяются запятыми. В качестве аргумента можно использ. др. функции и любы выраженея языка MATLAB.

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ.

Это обычно фун-и от одной переменной . Имя переменной к которой присвоив. значение функции распол. слева от знака равенства, если значения переменной (присваиваемой) не указыв. значение ф-и присваив-е служеб. переменной ans. Тип результата вычесления мат. функции совпадает с типом ее аргумента.

Abs.Синтаксис: у=abs (x)- абсолютное значение.Для массива действит. чисел х функция y=abs (x) возвращает массив у абсолютных значений элементов х. Для строковой переменной S (y=abs (s)) функция у=abs(x) возвращает вместо символов , включая пробелы их ABSCII- коды.

ANGLE аргумент комплексного числа . Синтаксис: P=angle (z). Для массива комплексных чисел Z эта функция возвращает

массив значений аргументов для элементов Z.

Для вычисления аргумента комплек. числа использ. след. соотношение:

angle (z)= atan 2 ( imag(z) , real (z)).

REAL Синтаксис : x=real (z) действит.и мни-

Imag Синтаксис: x=imag(z) мая части комплексного числа .Для массивов комплексных чисел z функция x=reab (z) возвращает массив действ. чисел, а x=imag(z) - массив мнимыхчастой элементов z.

SING Син.: s=sing (z) вычисление знака числа.

Для массива действю чисел х - эта функция возвращает массив S тех не размеров на месте положит. числа стоит 1, на месте отрицат. числа - -1 , на месте нулевого -0. Для массива комплек. чисел Z - эта функция возвращает массив комплек. чисел:

S= Z./ abs (z) , модуль к-рых равен 1.

ЭЛЕМЕНТЫ ОТЛАДКИ

DBSTOP Установить контрольную точку.Синтаксис: abstop in^2 имя М-файла>- позволяет задать режим отладки М- функции.Останавливает исполнение процедуры ипозволяет пользователю проверить любую локальную переменную и выполнить любую комманду.dbstop at <номер строки> in <имя Ф М-функции>.Устанавливает контрольную точку в заданной строке М файла.

dbstop if error

dbstop if naninf

dbstop if infnan

Устанавливают контр. точку по условию связанному с возникновением ошибки при исполнении модуля или при появлении результата nan или inf. Как только условие контр. точки выполняется на мониторе появляется спец. приглашение K>> для ввода комманды системы MATLAB.

DBCLEAR Удаление контр. точек.Синтаксис: dbclear in <имя функции> удаляет контр. точку в заданной строке определ М функции.

dbclear at <имя функции> in <имя функции> удаляет все контр. точки в данном М файле.

dbclear all in <имя файла>удаляет все контр. точки во всех активных М функциях.

dbclear all удаляет контр. точку перед первым исполняемым оператором данного М файла.

dbclaer if error удаляет контр. точки коммандой if error/

Файлы

В MATLAB особое значение имеют файлы двух типов — с расшире­ниями *.mat и *.m. Первые являются бинарными файлами, представ­ляющими запись сеанса (сессии) работы системы. Вторые представ­ляют собой текстовые файлы, содержащие внешние определения ко­манд и функций системы. Именно к ним относится большая часть команд и функций Toolbox — набор m-файлов стандартного расширения сис­темы, в том числе задаваемых пользователем для ре­шения своих специфических задач.

ТИПЫ М-ФАЙЛОВ

1. М сценарии или М списки

2. М функции

1. Характеристики М сценариев:

а) не допускает вход и выход аргументов

б) оперирует с данными из раб. области

в) предназначен для автоматизации последов-и шаблон. которые нужно выполнять много раз.

2. Характеристики М функции.

а) допускает вход и выход аргументов

б) по умолчанию внутр. переменные явл-ся локальными по отношению к функции

в) предназначена для раскрытия возможностей языка MATLAB, т. е. содержит библиотеки функций а также пакеты прикладных программ.

Структура М файла.

М-файл оформленный в виде функции состоит из следующих компонентов:

1. Строки определения ф-ций. Задают имя, кол-во и порядок следования входных и выходных аргументов

2. Первой строки комментария. Задают и определяет назначение функций. Вывод. на экран с помощью комманд look for или help<имя кат-а>.

3. Комментария, котор. выводится на экран вместе с первой строкой при использовании комманды help<имя функции>.

Тело ф-ции- это програмный код, который реалезует вычисления и присваивает значение выходным аргументам.

Стркутура М-функции.

М-ф-ция включает след. компоненты:

1. Строки определения ф-ции, котор. сообщают системе MATLAB, что файл является М-ф-цией,а также определяет список входных аргументов. Ключевое слово определения ф-ла как М-ф-ции- funktion. Если функция имеет более одного выходного аргумента список выходных аргументов помещается в квадратные скобки.

Если есть входные аргументы, то они помещаются в круглые скобки. Для отделения аргументов используются запятые.

2. Первая строка комментария. Начинается с символа % содержит текст комментария, в который обычно включается назначение ф-ции. Перв. строка текста появляется при наборе help funktion name.

3. Комментарий. Для М-файла можно создать on line подсказку вводя комментарии в более чем в одной строке. Тогда при вводе комманды help<имя ф-и> система MATLAB отображает комментарий, размещенный между строкой опред. фун-и и первой пустой строкой.

4. Оглавление каталога. Можно создать ком-й для целого каталога. Если создать файл с именем contents. m, который должен содержать только строки комментариев. Содержимое этого файла вывод-ся по комманде help<имя каталога>.

5. Тело функции, содержит программу на языке MATLAB, который выполняет вычисления и присваивает значение выходным аргументам. Операторы в теле ф-ции могут состоять из вызовов функции.

Имена М-функций.

Содержат ограничения имен переменных:

длина их не должна превышать 31 символа.

Единичная матрица.

DBSTEP Выполнить одну или несколько строк программы в режиме отладки.

Синтаксис: 1) dbstep

2) db step <количество строк>

3) db step in

1) допускают построчное исполнение М-ф информации 2)допускает исполнение сразу несколько строк 3)позволяет исполнить строку,

в к-рой присутствует вызов другой М-функции

DBCONT продолжить выполнение .Синтаксиса:dbcjnt
вызывает исполнение М-функций до следушей контрольной
точки установленной командой

dbstop или dbstep .

DBTIPE текстом М функции суказанием номеров

строк синтаксис:dbtype <имя функции>

dbtype <имя M-ф-и> <начало> <конец>

2 комманда позволяет ввести текст М-ф-и с указанием номеров строки. Для вывода части текста нужно указать диапозон выводимых номеров строк. Для вывода одной строки указать ее номер.

DBQUITE Выход из режима отладки. Синтаксис: dbquite. Эта комманда прекращает режим отладки и возвращает управление базисному модулю. Исполнение текущего М ф-а прерывается. Результаты не возвр.

ВРЕМЯ И ДАТЫ

Функции для обработки времени и дат.

Время и now текущее время и дата в файле

даты date текущая дата в форме строки

clock текущее время и дата в ф-и

Преобра date num перевести в N порядковой стр.

зование date str строковое представление даты

date vec векторное представление даты

Утили calendar календарь

ты weekday день недели

eamday последний день месяца

date tick дата с метками времени

Интер cputime время работы центр. процес-ра

валы tic

toc

E time

Задачи:

1) Построить график ф-ции y=sin(x)

z=cos(x)

x=[0;2п]

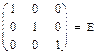
Задание

1) Вывести матрицу 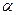размерами 3 на 3.

2) Протранспронировать матрицу и перевести ее в матрицу В.

Ввести матрицы А и В, получить их сумму и обозначить С.

Программа дискриминанта:

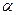=[1 2 3; 5 4 6; 7 8 9]

A=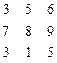

>> z=det(A)

z=-49

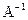- обратная матрица

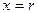cos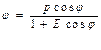

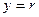
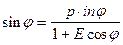
E= положительная гипербола

Е=0 парабола

Е<0- эллипс

Е= min- окруж.

Имена М-функций должны начинаться, остальные символы могут быть любой комбинацией букв. Расширение у М-ф-й -.m.

Если имя ф-ла и имя ф-ции разные, то исполняется имя ф-ла. Внутреннее имя игнорируется, хотя имя функции может не совпадать с именем ф-ла, желательно давать одинаковые имена ф-ям и ф-лам.

ОПЕРАТОР ПЕРЕКЛЮЧЕНИЯ

SWITCH... CASE... OTHERWISE... END

switch<выражение>case<значение1> инструкции otherwise инструкции end

Этот оператор выполняет ветвление в зависимости от значения искомой переменной или выражения.

Оператор переключения включает:

1) Заголовок switch за которым следует выполняемое выражение.

2) Произвольное количество группы case.

Заголовок группы состоит из слова case за которым следует возможное значение выр-я, расположенное на одной строке.

МАТРИЧНОЕ ДЕЛЕНИЕ

Имеется 2 символа матричного деления- левое и правое (\ и /).

X=A\B решение уравнения A*X=B

X=A/B решение уравнения X*A=B

Левое деление, \, определено когда В имеет столько же строк сколько А.

Правое деление, /, может быть определено в виде левого деления В/A=(A\B).

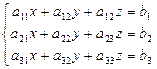
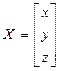
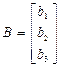
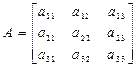
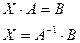
(Инвертированная матрица )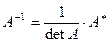

X=B/A

Задача:

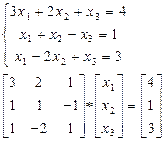
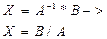
Блокнот М-file

% Лабораторная работа 1

A=[5 8 -1; 1 2 1; 2 -3 2]

B=[-7; 1; 9;]

S=B\A

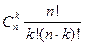
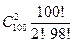
k=0;

for x=1;

k=k+x;

end

n=k

Общее число элементов 5,используют 80 байтов.

Сопутствуещие функции:EXP,LOG,SQRTM.

EXP Экспоненциальная функция

Синтаксис:

V=exp(Z)

Описание:

Функция V=exp(Z) вычесляет экспоненты значений элементов массива Z.

Для комплексных значений z=x+iy справедлива формула Эйлера

e^z=e^x(cos(y)+i sin(y)).

Вычесление экспоненты от матрицы реализовано с помощью специальной функции expm.

Cопутствующие функции: LOG,LOG2,LOG10,EXPM.

LOG Функция натурального логарифма

Cинтаксис:

V=log(Z)

Описание:

Функция V=log(Z) вычесляет натуральный логарифм значений элементов массива Z.

Длякомплексныч значений z=x+iy справедлива формула

ln(z)=ln(abs(z))+i atan2(y,x).

Вычесление функции натурального логарифма от матрицы реализовано с помощью специальной функции logm.

Пример:

Одна из возможностей вычесления значения числа p-это вычислить

log(-1)

log(-1)

ans=

0+3.141592653589793е+000i

Cопутствуещие функции:EXP,LOG2,LOG!0,LOGM.

POW2 Экспонента по основанию 2

Синтаксис:

V=pow2(Z) X=pow2([M,P])

Описание:

Функция V=pow2(Z) вычесляет массив степеней 2.Z.

Функция X=pow2([M,P]) для действительных массивов М и Р вычесляет массив X=M.*(2.P).

Пример:

Для компьютеров с IEEE- арифметикой, в которых определены объекты eps, realmax и realmin, функция x=pow2([m.p]) вычесляет следуещие величины :

m	p	x
1/2
pi/4		pi
-3/4		-3
1/2	-51	eps
1-eps/2		realmax
1/2	-1021	realmin

Cопутствующие функции:LOG2,NEXTPOW2.

NEXTPOW2 Ближайщая степень по основанию 2

Синтаксис:

p=nextpow2(n)

p=nextpow2(x)

Описание:

Функция p=nextpow2(n) возвращает такой показатель степени p, что 2 pіn.

Футкция p=ntxtpow2(x) для одномерного массива х возвращает значение nextpow2(length(x)). Эта операция широко применяется при вычеслении быстрого

преобразования Фурье.

Пример:

Для любого целого числа n в диапазоне от 513 до 1024 функция nextpow2(n) возвращает

значения 10.

Сопутствующие функции:FFT,LOG2,POW2.

LOG2 Функция логарифма

Синтаксис:

V=log2(Z) [M,P]=log2(x)

Описание:

Функция V=log2(Z) вычесляет логарифм пооснованию 2 от значений элементов массива Z.

Функция [M,P]=log2(X) для массива Х действительных чисел возвращает массив М значений мантисс и целочисленный массив P показательстепеней,позволяющих

представить любой элементу соответствует представление {f=0, e=0}.

Примеры:

Для компьютеров с IEEE-арифметикой, в которых определены объекты eps, realmax,realmin,

функция log2 вычесляет следуещие величины:

log2(eps)=-52, log2(realmax)=1024, log2(realmin)=-1022,

а функция [M,P}=log2(X) строет следующие представления чисел

х m p

1 1/2 1

pi pi/4 2

-3 -3/4 2

eps 1/2 -51

realmax 1-eps/2 1021

realmin 1/2 -1021

Сопутствующие функции:LOG2, NEXTPOW2, POW2.

LOG !0 Функция логарифма

Синтаксис:

V=log 10(Z)

Описание:

Функция V=log 10(Z) вычесляет логарифм по основанию 10 от значений элементов массива Z

Примеры:

Для компьютеров с IEEE-арифметикой, в которых определены объекты eps, realmax,

realmin, функция log 10 вычесляет следующие величины:

log 10(eps) log 10(realmax) log 10(realmin)

-15.6536 308.2547 -307.652

Сопутствующие функции: EXP, LOG2, LOGM, POW2.

Тригонометрические функции

SIN, SINH Функции синуса

Синтаксис:

V=sin(Z)

V=sin(Z)

Описание:

Функция V=sin(Z) вычесляет синус от значение элементов массива Z.

Функция V=sinh(Z) вычесляет гиперболический синус от значений элементов массива Z.

Массив Z допускает комплексные значения; углы измераются в радионах.

Для вычесления функции от матрицы следует применять специальные функции funm или

expm.

Алгоритм:

Для вычесления функций синуса используются следуещие соотнощения:

sin(x+iy)=sin(x)ch(y)+icos(x)sh(y);

sh(z)=e^z-e^-z ;

sin(z)=-i sh(iz).

Cопутствующие функции: ASIN, ASIMH, CSC, CSCH, ACSC, ACSCH, EXPM, FUNM.

ASIN, ASINH Функция обратного синуса

Синтаксис:

V=asin(Z)

V+asinh(Z)

Описание:

Функция V=asin(Z) вычесляет обратную функцию синуса от значение элементов массива Z.

Функция V=asinh(Z) вычесляет обратную функцию гиперболического синуса от значений

элемента массива Z.

Массив Z допускает комплексные значения; углы V измеряются в радианах.

Функция Y=asin(X) для действительных значений -1Ј х Ј1 определена в интервале

-p/2Ј x Јp/2.

Для вычисления функций от матрицы следует применять специальную функцию funm.

Алгаритм:

Для вычисления функций обратного синуса используются следующие соотношения :

arsh(z)=ln[z+(1+z^2) ];

arcsin(z)=-i arsh(iz).

Cопутствующие функции

МАТЕМАТИЧЕСКИЕ ФУНКЦИИ

В системе MATLAB имеется обширные библиотека матем-ких функций. Каждой функции соответствует определенное имя. Функция ставит в соответствие значениям своих аргументов значение результата.

Аргументы функции всегда указываются в круглых скобках после имени функции и, если их больше одного, разделяються запятыми. В качестве аргументов могут использоватся другие функции и любые выражения языка MATLAB (при условии соответствия типов аргументов).

Элементарные функции

Элементарная математическая функция-это, как правило, функция от одной переменной, и в этом случае устанавливается соответствие между массивами значений аргумента и результата.

Аргумент указывается в круглых скобках после имени функции. Имя переменной, которой присваивается значения функции, располагаются слева от знака равенства. Если имя присваиваемой переменной не указано, значение функции присваиваетсяслужебной переменной ans.

Тип результата вычесления математической функции всегда соовпадает с типом ее аргумента . Например, если аргументом функции является вектор-столбец, то значением этой функции также будет вектор-столбец.

Рассмотрим встроенные математические функции системы MATLAB, которые применяются к числам, скалярным переменным и к массивам (поэлементно).

Базовые функции

ABS Абсолютное значение

Синтаксис:

Y=abs(X)

Описание:

Для массива действительных чисел Х функции Y=abs(X) возвращает массив Y абсолютных значений элементов Х.

Для массива комплексных чисел Z функция Y=abs(Z) возвращает массив Y модулей комплексных элементов Z.

Для строковой переменной S функция Y=abs(S) возвращает вместо символов, включая пробелы, их ASCII-коды.

Пример:

abs(-5)=5

abs(3+4i)=5

ascii=abs(‘3+41’)

ascii=51 32 43 32 52 105

setstr(ascii)

ans=3+41

Сопутствующие функции: SIGN, ANGLE, REAL, IMAG, SETSTR.