Кинематика рядного зубчатого механизма.

Сложные зубчатые механизмы

Сложными зубчатыми механизмами называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным и (или) параллельным соединением простейших типовых зубчатых механизмов.
Механизмы, в которых кинематические цепи образуют один или несколько замкнутых контуров и в которых входной поток механической мощности в процессе передачи и преобразования делится на несколько потоков, а затем суммируется на выходном звене, называются многопоточными механизмами. Распределение передаваемых усилий по нескольким кинематическим парам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный контакт звеньев механизма существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Однако, за счет образования в структуре механизма внутренних контуров, число избыточных или пассивных связей в механизме увеличивается. Поэтому при изготовлении и сборке механизма необходимо либо повышать точность деталей, либо увеличивать зазоры в кинематических парах.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. К типовым планетарным механизмам относятся:

• однорядный планетарный механизм;
• двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением
• двухрядный планетарный механизм с двумя внешними зацеплениями;
• двухрядный планетарный механизм с двумя внутренними зацеплениями.

Элементы планетарного механизма имеют специальные названия:

• зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным";
• колесо с внутренними зубьями называют "короной" или "эпициклом";
• колеса, оси которых подвижны, называют "сателлитами";
• подвижное звено, на котором установлены сателлиты, называют "водилом" . Звено водила принято обозначать не цифрой, а латинской буквой h.

В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.

Таблица 15.1

Типовые планетарные механизмы

№	Структурная схема механизма	Uред	КПД
		3....10	0.97....0.99
		7....16	0.96....0.98
		25....30	0.9....0.3
		30....300	0.9....0.3

Формула Виллиса.

Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним зацеплением (см. рис. 15.3). Число подвижностей в этом механизме равно 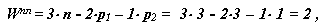то есть для получения определенности движения звеньев механизма необходимо сообщить независимые движения двум его звеньям. Рассмотрим движение звеньев механизма относительно стойки и относительно водила. Угловые скорости звеньев в каждом из рассматриваемых движений приведены в таблице 15.2.

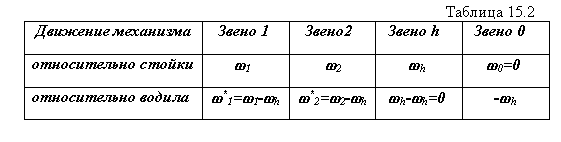
В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось зубчатого колеса 2 подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.

Вопросы для самопроверки

- Какой зубчатый механизм называется сложным?

- Какой механизм называется планетарным?

- Как определить передаточное отношение одной из схем планетарного редуктора аналитическим способом ?

- Как используются графический и аналитический способы для определения угловых скоростей звеньев планетарных зубчатых механизмов?

- Как устанавливаются кинематические зависимости в планетарном зубчатом механизме с коническими колесами?

- Как используется графический способ для определения угловых скоростей звеньев дифференциалов?

- Какова цель применения метода обращения движения при кинематическом анализе планетарных механизмов?

- Что отличает передаточное отношение от передаточного числа?

- Как определяют передаточное отношение многоступенчатого рядового механизма? Какое участие в формуле передаточного отношения принимают числа зубьев связанных колес?

- Какие звенья планетарного механизма называют центральными?

- Что представляет собой «обращенный механизм»?

- Запишите формулы Виллиса: для дифференциальной ступени типа 2КН; для планетарной ступени типа 3К.

- Как вычисляют передаточное отношение комбинированного механизма с последовательным соединением ступеней?

- Опишите методику кинематического анализа замкнутого дифференциального механизма.

Вопросы для самопроверки

Задача 1

Сколько оборотов сделает колесо , когда водило H совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 2(см. рисунок к задаче 1)

Сколько оборотов сделает водило H, когда колесо совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 3(см. рисунок к задаче 1)

Определить величину передаточного отношения , если соотношение чисел зубьев колес .

Задача 4(см. рисунок к задаче 1)

Сколько оборотов сделает колесо относительно водила H, когда водило совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 5

Определить величину передаточного отношения , если соотношение чисел зубьев колес .

Задача 6(см. рисунок к задаче 5)

Сколько оборотов сделает водило H, когда колесо совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 7(см. рисунок к задаче 5)

Сколько оборотов сделает колесо , когда водило H совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 8(см. рисунок к задаче 5)

Сколько оборотов сделает колесо относительно водила H, когда последнее совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 9

Найти угловую скорость сателлита , если =1 c^-1, =-1 c^-1. Соотношение чисел зубьев колес .

Задача 10

Для планетарной ступени комбинированного редуктора написать формулы для проверки условий соосности, соседства и сборки, выразив их через числа зубьев колес.

Задача 11(см. рисунок к задаче 10)

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес.

Задача 12

Для планетарной ступени комбинированного редуктора написать формулы для проверки условий соосности, соседства и сборки, выразив их через числа зубьев колес.

Задача 13(см. рисунок к задаче 12)

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес.

Задача 14

Для планетарной ступени комбинированного редуктора написать формулы для проверки условий соосности, соседства и сборки, выразив их через числа зубьев колес.

Задача 15(см. рисунок к задаче 3.14)

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес; рассчитать величину при =18; =36; =77; =22; =21; =75.

Задача 16(см. рисунок к задаче 14)

Для комбинированного редуктора установить условие, при выполнении которого его передаточное отношение .

Задача 17

Считая, что =3, найти частоту относительного вращения , если выходной вал B вращается с частотой =-10 об/мин.

Задача 18

Считая, что , найти частоту относительного вращения , если выходной вал вращается с частотой =-20 об/мин.

Задача 19

Формулу передаточного отношения редуктора 3К выразить через числа зубьев колес.

Задача 20(см. рисунок к задаче 19)

Для редуктора 3К написать условия соосности, соседства (в предположении, что ) и сборки, выразив их через числа зубьев колес.

Задача 21

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес.

Задача 22

Для непланетарной части комбинированного редуктора написать формулы для проверки условий соосности, соседства и сборки, выразив их через числа зубьев колес.

Задача 23

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес. Рассчитать величину при .

Задачи 24 – 26

Формулу передаточного отношения каждого из редукторов типа 4К выразить через числа зубьев колес.

Задача 27

Для планетарного двухступенчатого редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес.

Задача 28(см. рисунок к задаче 27)

Для планетарного двухступенчатого редуктора определить величину передаточного отношения при , .

Задача 29

Вал B редуктора вращается с частотой =100 об/мин, передаточное отношение редуктора =-25. Найти частоту вращения вала колеса относительно водила H, если соотношение чисел зубьев .

Задача 30

Вал B редуктора вращается с частотой =100 об/мин; найти частоту вращения колеса относительно вала водила H, если соотношение чисел зубьев .

Задача 31

Вал B редуктора вращается с частотой =40 об/мин, передаточное отношение редуктора = 25; найти частоту вращения колеса относительно вала A, если соотношение чисел зубьев .

Задача 32

Вал B редуктора вращается с частотой =100 об/мин, передаточное отношение редуктора = 25; найти частоту вращения колеса относительно вала A, если соотношение чисел зубьев .

Задача 33

Вал B редуктора вращается с частотой =40 об/мин, передаточное отношение редуктора = 25; найти частоту вращения колеса относительно вала A, если соотношение чисел зубьев .

Задача 34

Выходной вал B редуктора вращается с частотой =40 об/мин; найти частоту вращения колес и относительно вала водила, если соотношение чисел зубьев .

Задача 35

Выходной вал B редуктора вращается с частотой =40 об/мин, передаточное отношение редуктора = 31; найти частоту вращения колес и относительно входного вала, если соотношение чисел зубьев .

Задача 36

Передаточное отношение редуктора =-40, соотношение чисел зубьев , частота вращения входного вала =1400 об/мин; определить относительную частоту вращения .

Задача 37

Вал A редуктора вращается с частотой =1500 об/мин, передаточное отношение =40. Определить частоту вращения колеса относительно вала A, если =12.

Задача 38(см. рисунок к задаче 37)

Вал A редуктора вращается с частотой =1500 об/мин, передаточное отношение =40. Определить частоту вращения колеса относительно водила H, если .

Задача 39

Выходной вал B редуктора вращается с частотой =-40 об/мин, передаточное отношение редуктора =-35; найти частоту вращения водила H относительно вала A, если соотношение чисел зубьев .

Задача 40(см рисунок к задаче 39)

Входной вал A редуктора вращается с частотой =1400 об/мин, передаточное отношение редуктора =-35; найти частоту вращения водила H относительно вала A, если соотношение чисел зубьев .

Задача 41

Определить частоту вращения колеса относительно вала A, если и передаточное отношение редуктора =40. Выходной вал редуктора вращается с частотой =50 об/мин.

Задача 42

Определить частоту вращения колеса относительно вала водила , если передаточное отношение и частота вращения выходного вала =100 об/мин

Задача 43

Частота вращения вала A редуктора , передаточное отношение ; определить частоту относительного вращения , если .

Задача 44

Частота вращения вала A редуктора =1400 об/мин, передаточное отношение ; определить частоту вращения водила , если .

Задача 45

Передаточное отношение редуктора выразить через числа зубьев колес.

Задача 46(см. рисунок к задаче 44)

Рассчитать передаточное отношение редуктора при следующих соотношениях чисел зубьев: ; .

Задача 47

Водило OAB планетарного механизма вращается с угловой скоростью =15 рад/с, колесо неподвижно. Определить угловые скорости сателлитов и , если числа зубьев колес =30, =20.

Задача 48

Рассчитать передаточное отношение редуктора, если числа зубьев колес равны: =33; =36.

Задача 49(см. рисунок к задаче 47)

Подобрать числа зубьев колес и редуктора, обеспечивающих получение передаточного отношения , если разность .

Сложные зубчатые механизмы

Сложными зубчатыми механизмами называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным и (или) параллельным соединением простейших типовых зубчатых механизмов.
Механизмы, в которых кинематические цепи образуют один или несколько замкнутых контуров и в которых входной поток механической мощности в процессе передачи и преобразования делится на несколько потоков, а затем суммируется на выходном звене, называются многопоточными механизмами. Распределение передаваемых усилий по нескольким кинематическим парам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный контакт звеньев механизма существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Однако, за счет образования в структуре механизма внутренних контуров, число избыточных или пассивных связей в механизме увеличивается. Поэтому при изготовлении и сборке механизма необходимо либо повышать точность деталей, либо увеличивать зазоры в кинематических парах.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. К типовым планетарным механизмам относятся:

• однорядный планетарный механизм;
• двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением
• двухрядный планетарный механизм с двумя внешними зацеплениями;
• двухрядный планетарный механизм с двумя внутренними зацеплениями.

Элементы планетарного механизма имеют специальные названия:

• зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным";
• колесо с внутренними зубьями называют "короной" или "эпициклом";
• колеса, оси которых подвижны, называют "сателлитами";
• подвижное звено, на котором установлены сателлиты, называют "водилом" . Звено водила принято обозначать не цифрой, а латинской буквой h.

В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.

Таблица 15.1

Типовые планетарные механизмы

№	Структурная схема механизма	Uред	КПД
		3....10	0.97....0.99
		7....16	0.96....0.98
		25....30	0.9....0.3
		30....300	0.9....0.3

Кинематика рядного зубчатого механизма.

Рядным зубчатым механизмом называется сложный зубчатый механизм с неподвижными осями колес, образованный последовательным соединением нескольких простых зубчатых механизмов. Рассмотрим кинематику рядного механизма составленного из двух зубчатых передач: одной внешнего зацепления и одной внутреннего зацепления. Схема механизма изображена на рис. 15.1.

Напоминание: Для вращательного движения твердого тела относительно оси проходящей через точку А. Примем для размеров масштаб μl, мм/м, а для линейных скоростей - масштаб μV, мм/м∙с-1. Угловая скорость звена i равна

Таким образом при графическом кине матическом анализе угловая скорость звена равна произведению тангенса угла наклона прямой распределения лиейных скоростей на отношение масштабов длин и скоростей.