Часть 1. Теория Автоматического Управления (ТАУ)

Часть 1. Теория Автоматического Управления (ТАУ)

Лекция 1. Основные термины и определения ТАУ. (2 часа)

Основные понятия.

Системы управления современными химико-технологическими процессами характеризуются большим количеством технологических параметров, число которых может достигать нескольких тысяч. Для поддержания требуемого режима работы, а в конечном итоге – качества выпускаемой продукции, все эти величины необходимо поддерживать постоянными или изменять по определенному закону.

Физические величины, определяющие ход технологического процесса, называются параметрами технологического процесса. Например, параметрами технологического процесса могут быть: температура, давление, расход, напряжение и т.д.

Параметр технологического процесса, который необходимо поддерживать постоянным или изменять по определенному закону, называется регулируемой величиной или регулируемым параметром.

Значение регулируемой величины в рассматриваемый момент времени называется мгновенным значением.

Значение регулируемой величины, полученное в рассматриваемый момент времени на основании данных некоторого измерительного прибора называется ее измеренным значением.

Пример 1.Схема ручного регулирования температуры сушильного шкафа.

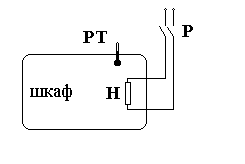Рис. 1.1

Требуется вручную поддерживать температуру в сушильном шкафу на уровне Т_зад.

Человек-оператор в зависимости от показаний ртутного термометра РТ включает или выключает нагревательный элемент Н с помощью рубильника Р. ¨

На основе данного примера можно ввести определения:

Объект управления (объект регулирования, ОУ) – устройство, требуемый режим работы которого должен поддерживаться извне специально организованными управляющими воздействиями.

Управление – формирование управляющих воздействий, обеспечивающих требуемый режим работы ОУ.

Регулирование – частный вид управления, когда задачей является обеспечение постоянства какой-либо выходной величины ОУ.

Автоматическое управление – управление, осуществляемое без непосредственного участия человека.

Входное воздействие (Х) – воздействие, подаваемое на вход системы или устройства.

Выходное воздействие (Y) – воздействие, выдаваемое на выходе системы или устройства.

Внешнее воздействие – воздействие внешней среды на систему.

Структурная схема системы регулирования к примеру 1 изображена на рис. 1.2.

Пример 2.Схема автоматического регулирования температуры сушильного шкафа.

В схеме используется ртутный термометр с контактами РТК. При повышении температуры до заданной контакты замыкаются столбиком ртути, катушка релейного элемента РЭ возбуждается и цепь нагревателя Н размыкается контактом РЭ. При понижении температуры контакты термометра размыкаются, реле обесточивается, возобновляя подачу энергии на объект (см. рис. 1.3). ¨

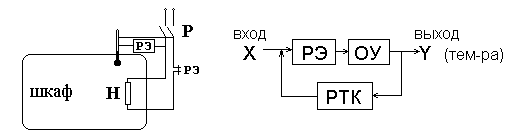Рис. 1.3

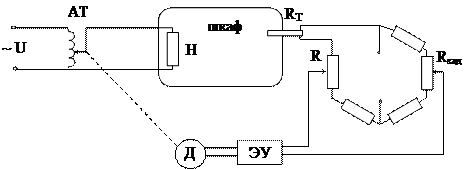
Пример 3.Схема АСР температуры с измерительным мостом.

При температуре объекта, равной заданной, измерительный мост М (см. рис. 1.4) уравновешен, на вход электронного усилителя ЭУ сигнал не поступает и система находится в равновесии. При отклонении температуры изменяется сопротивление терморезистора R_Т и равновесие моста нарушается. На входе ЭУ появляется напряжение, фаза которого зависит от знака отклонения температуры от заданной. Напряжение, усиленное в ЭУ, поступает на двигатель Д, который перемещает движок автотрансформатора АТ в соответствующую сторону. При достижении температуры, равной заданной, мост сбалансируется и двигатель отключится.

Рис. 1.4

Величина заданного значения температуры устанавливается с помощью резистора R_зад. ¨

Исходя из описанных примеров, можно определить типовую структурную схему одноконтурной АСР (см. рис. 1.5). Принятые обозначения:

x - задающее воздействие (задание), e = х - у - ошибка регулирования, u - управляющее воздействие, f - возмущающее воздействие (возмущение).

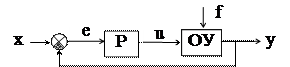Рис. 1.5

Определения:

Задающее воздействие (то же, что входное воздействие Х) - воздействие на систему, определяющее требуемый закон изменения регулируемой величины).

Управляющее воздействие (u) - воздействие управляющего устройства на объект управления.

Управляющее устройство (УУ) - устройство, осуществляющее воздействие на объект управления с целью обеспечения требуемого режима работы.

Возмущающее воздействие (f) - воздействие, стремящееся нарушить требуемую функциональную связь между задающим воздействием и регулируемой величиной.

Ошибка управления (е = х - у) - разность между предписанным (х) и действительным (у) значениями регулируемой величины.

Регулятор (Р) - комплекс устройств, присоединяемых к регулируемому объекту и обеспечивающих автоматическое поддержание заданного значения его регулируемой величины или автоматическое изменение ее по определенному закону.

Автоматическая система регулирования (АСР) - автоматическая система с замкнутой цепью воздействия, в котором управление (u) вырабатывается в результате сравнения истинного значения у с заданным значением х.

Дополнительная связь в структурной схеме АСР, направленная от выхода к входу рассматриваемого участка цепи воздействий, называется обратной связью (ОС). Обратная связь может быть отрицательной или положительной.

Классификация АСР.

1. По назначению (по характеру изменения задания):

· стабилизирующая АСР - система, алгоритм функционирования которой содержит предписание поддерживать регулируемую величину на постоянном значении (x = const);

· программная АСР - система, алгоритм функционирования которой содержит предписание изменять регулируемую величину в соответствии с заранее заданной функцией (x изменяется программно);

· следящая АСР - система, алгоритм функционирования которой содержит предписание изменять регулируемую величину в зависимости от заранее неизвестной величины на входе АСР (x = var).

2. По количеству контуров:

· одноконтурные - содержащие один контур,

· многоконтурные - содержащие несколько контуров.

3. По числу регулируемых величин:

· одномерные - системы с 1 регулируемой величиной,

· многомерные - системы с несколькими регулируемыми величинами.

Многомерные АСР в свою очередь подразделяются на системы:

а) несвязанного регулирования, в которых регуляторы непосредственно не связаны и могут взаимодействовать только через общий для них объект управления;

б) связанного регулирования, в которых регуляторы различных параметров одного и того же технологического процесса связаны между собой вне объекта регулирования.

4. По функциональному назначению:

АСР температуры, давления, расхода, уровня, напряжения и т.д.

5. По характеру используемых для управления сигналов:

· непрерывные,

· дискретные (релейные, импульсные, цифровые).

6. По характеру математических соотношений:

· линейные, для которых справедлив принцип суперпозиции;

· нелинейные.

Принцип суперпозиции (наложения): Если на вход объекта подается несколько входных воздействий, то реакция объекта на сумму входных воздействий равна сумме реакций объекта на каждое воздействие в отдельности:

L(х₁ + х₂) = L(х₁) + L(х₂),

где L - линейная функция (интегрирование, дифференцирование и т.д.).

7. По виду используемой для регулирования энергии:

· пневматические,

· гидравлические,

· электрические,

· механические и др.

8. По принципу регулирования:

· по отклонению:

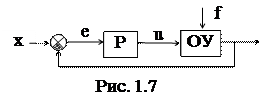Подавляющее большинство систем построено по принципу обратной связи - регулирования по отклонению (см. рис. 1.7).

Элемент называется сумматором. Его выходной сигнал равен сумме входных сигналов. Зачерненный сектор говорит о том, что данный входной сигнал надо брать с противоположным знаком.

· по возмущению.

Данные системы могут быть использованы в том случае, если есть возможность измерения возмущающего воздействия (см. рис. 1.8). На схеме обозначен К - усилитель с коэффициентом усиления К.

· комбинированные - сочетают в себе особенности предыдущих АСР.

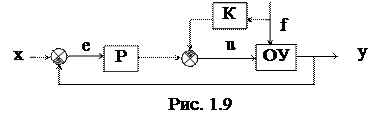
Данный способ (см. рис. 1.9) достигает высокого качества управления, однако его применение ограничено тем, что возмущающее воздействие f не всегда можно измерить.

Основные модели.

Работу системы регулирования можно описать словесно. Так, в п. 1.1 описана система регулирования температуры сушильного шкафа. Словесное описание помогает понять принцип действия системы, ее назначение, особенности функционирования и т.д. Однако, что самое главное, оно не дает количественных оценок качества регулирования, поэтому не пригодно для изучения характеристик систем и построения систем автоматизированного управления. Вместо него в ТАУ используются более точные математические методы описания свойств систем:

· статические характеристики,

· динамические характеристики,

· дифференциальные уравнения,

· передаточные функции,

· частотные характеристики.

В любой из этих моделей система может быть представлена в виде звена, имеющего входные воздействия Х, возмущения F и выходные воздействия Y

Под влиянием этих воздействий выходная величина может изменяться. При этом при поступлении на вход системы нового задания она должна обеспечить с заданной степенью точности новое значение регулируемой величины в установившемся режиме.

Установившийся режим - это режим, при котором расхождение между истинным значением регулируемой величины и ее заданным значением будет постоянным во времени.

Статические характеристики.

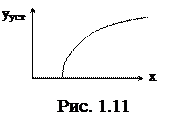Статической характеристикой элемента называется зависимость установившихся значений выходной величины от значения величины на входе системы, т.е.

y_уст = j(х).

Статическую характеристику (см. рис. 1.11) часто изображают графически в виде кривой у(х).

Статическим называется элемент, у которого при постоянном входном воздействии с течением времени устанавливается постоянная выходная величина. Например, при подаче на вход нагревателя различных значений напряжения он будет нагреваться до соответствующих этим напряжениям значений температуры.

Астатическим называется элемент, у которого при постоянном входном воздействии сигнал на выходе непрерывно растет с постоянной скоростью, ускорением и т.д.

Линейным статическим элементом называется безинерционный элемент, обладающий линейной статической характеристикой:

у_уст = К*х + а₀.

Как видно, статическая характеристика элемента в данном случае имеет вид прямой с коэффициентом наклона К.

Линейные статические характеристики, в отличие от нелинейных, более удобны для изучения благодаря своей простоте. Если модель объекта нелинейна, то обычно ее преобразуют к линейному виду путем линеаризации.

САУ называется статической, если при постоянном входном воздействии ошибка управления е стремится к постоянному значению, зависящему от величины воздействия.

САУ называется астатической, если при постоянном входном воздействии ошибка управления стремится к нулю вне зависимости от величины воздействия.

Передаточные функции.

Примеры типовых звеньев.

Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе. Соотношение входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями.

Простейшие типовые звенья:

· усилительное,

· интегрирующее,

· дифференцирующее,

· апериодическое,

· колебательное,

· запаздывающее.

1) Усилительное звено.

Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления.

Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз (см. рис. 1.15).

Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др.

2) Интегрирующее.

2.1) Идеальное интегрирующее.

Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины.

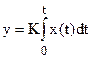; W(s) =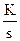

При подаче на вход звена воздействия выходной сигнал постоянно возрастает (см. рис. 1.16).

Это звено астатическое, т.е. не имеет установившегося режима.

2.2) Реальное интегрирующее.

Передаточная функция этого звена имеет вид:

W(s) = .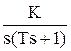

Переходная характеристика в отличие от идеального звена является кривой (см. рис. 1.17).

Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора.

3) Дифференцирующее.

3.1) Идеальное дифференцирующее.

Выходная величина пропорциональна производной по времени от входной:

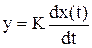; W(s) = K*s

При ступенчатом входном сигнале выходной сигнал представляет собой импульс (d-функцию).

3.2) Реальное дифференцирующее.

Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям. Переходная характеристика и передаточная функция этого звена имеют вид:

W(s) = .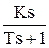

4) Апериодическое (инерционное).

Этому звену соответствуют ДУ и ПФ вида:

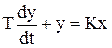; W(s) = .

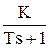Определим характер изменения выходной величины этого звена при подаче на вход ступенчатого воздействия величины х₀.

Изображение ступенчатого воздействия: X(s) = 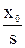. Тогда изображение выходной величины:

Y(s) = W(s) X(s) = 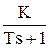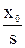= K x₀ .

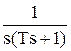Разложим дробь на простые:

= + = = - = -

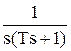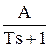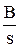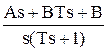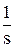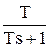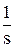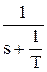
Оригинал первой дроби по таблице: L^-1{ 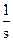} = 1, второй:

L^-1{ } = .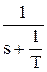

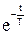Тогда окончательно получаем:

y(t) = K x₀ (1 - ).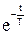

Постоянная Т называется постоянной времени.

Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону (см. рис. 1.19).

5) Колебательное звено имеет ДУ и ПФ вида

,

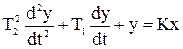W(s) = .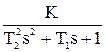

При подаче на вход ступенчатого воздействия амплитудой х₀ на переходная кривая будет

иметь один из двух видов: апериодический (при Т₁ ³ 2Т₂) или колебательный (при Т₁ < 2Т₂).

6) Запаздывающее.

y(t) = x(t - t), W(s) = e^-ts.

Выходная величина у в точности повторяет входную величину х с некоторым запаздыванием t. Примеры: движение груза по конвейеру, движение жидкости по трубопроводу.

Соединения звеньев.

Поскольку исследуемый объект в целях упрощения анализа функционирования разбит нами на звенья, то после определения передаточных функций для каждого звена встает задача объединения их в одну передаточную функцию объекта. Вид передаточной функции объекта зависит от последовательности соединения звеньев:

1) Последовательное соединение.

W_об = W₁^.W₂^.W₃…

При последовательном соединении звеньев их передаточные функции перемножаются.

2) Параллельное соединение.

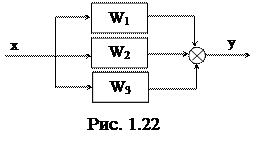W_об = W₁ + W₂ + W₃ + …

При параллельном соединении звеньев их передаточные функции складываются.

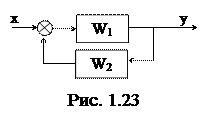3) Обратная связь

Передаточная функция по заданию (х):

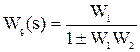
«+» соответствует отрицательной ОС,

«-» - положительной.

Для определения передаточных функций объектов, имеющих более сложные соединения звеньев, используют либо последовательное укрупнение схемы, либо преобразуют по формуле Мезона.

Передаточные функции АСР.

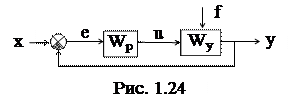Для исследования и расчета структурную схему АСР путем эквивалентных преобразований приводят к простейшему стандартному виду «объект - регулятор».

Это необходимо, во-первых, для того, чтобы определить математические зависимости в системе, и, во-вторых, как правило, все инженерные методы расчета и определения параметров настройки регуляторов применены для такой стандартной структуры.

В общем случае любая одномерная АСР с главной обратной связью путем постепенного укрупнения звеньев может быть приведена к такому виду.

Если выход системы у не подавать на ее вход, то мы получим разомкнутую систему регулирования, передаточная функция которой определяется как произведение:

W_¥ = W_p^.W_y

(W_p - ПФ регулятора, W_y - ПФ объекта управления).

То есть последовательность звеньев W_p и W_y может быть заменена одним звеном с W_¥. Передаточную функцию замкнутой системы принято обозначать как Ф(s). Она может быть выражена через W_¥:

Ф_з(s) = = .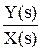

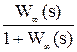(далее будем рассматривать только системы с обратной отрицательной связью, поскольку они используются в подавляющем большинстве АСР).

Данная передаточная функция Ф_з(s) определяет зависимость у от х и называется передаточной функцией замкнутой системы по каналу задающего воздействия (по заданию).

Для АСР существуют также передаточные функции по другим каналам:

Ф_e(s) = 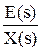= 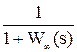- по ошибке,

Ф_в(s) = 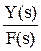= 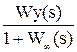- по возмущению.

Поскольку передаточная функция разомкнутой системы является в общем случае дробно-рациональной функцией вида W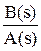_¥ = , то передаточные функции замкнутой системы могут быть преобразованы:

Ф_з(s) = 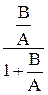= 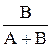, Ф_e(s) = = .

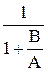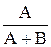Как видно, эти передаточные функции отличаются только выражения ми числителей. Выражение знаменателя называется характеристическим выражением замкнутой системы и обозначается как D_з(s) = A(s) + B(s), в то время как выражение, находящееся в числителе передаточной функции разомкнутой системы W_¥, называется характеристическим выражением разомкнутой системы B(s).

Частотные характеристики.

Примеры ЛЧХ.

1. Фильтр низких частот (ФНЧ)

ЛАЧХ ЛФЧХ Пример цепи

Фильтр низких частот предназначен для подавления высокочастотных воздействий.

2. Фильтр высоких частот (ФВЧ)

ЛАЧХ ЛФЧХ Пример цепи

Фильтр высоких частот предназначен для подавления низкочастотных воздействий.

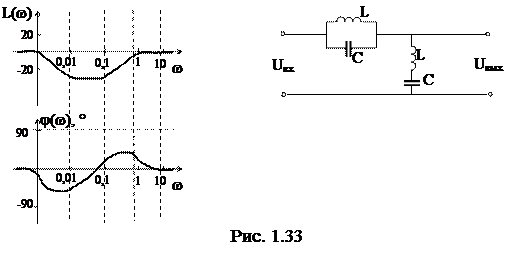
3. Заградительный фильтр.

Заградительный фильтр подавляет только определенный диапазон частот

ЛАЧХ и ЛФЧХ Пример цепи

.

Лекция 3. Качество процессов управления.(2 часа)

Критерии устойчивости.

Устойчивость.

Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменение его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.

Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости:

1) корневой критерий,

2) критерий Стодолы,

3) критерий Гурвица,

4) критерий Найквиста,

5) критерий Михайлова и др.

Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем. Критерий Гурвица является алгебраическим и разработан для определения устойчивости замкнутых систем без запаздывания. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.

Корневой критерий.

Корневой критерий определяет устойчивость системы по виду передаточной функции. Динамической характеристикой системы, описывающей основные поведенческие свойства, является характеристический полином, находящийся в знаменателе передаточной функции. Путем приравнивания знаменателя к нулю можно получить характеристическое уравнение, по корням которого определить устойчивость.

Корни характеристического уравнения могут быть как действительные, так и комплексные и для определения устойчивости откладываются на комплексной плоскости (см. рис. 1.34).

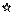(Символом обозначены корни уравнения).

Виды корней характеристического уравнения:

- Действительные:

положительные (корень № 1);

отрицательные (2);

нулевые (3);

- Комплексные

комплексные сопряженные (4);

чисто мнимые (5);

По кратности корни бывают:

одиночные (1, 2, 3);

сопряженные (4, 5): s_i = a ± jw;

кратные (6) s_i = s_i+1 = …

Корневой критерий формулируется следующим образом:

Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости. Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (не зависимо от числа корней в левой), то система является неустойчивой.

Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.

Пример 3.1.Передаточная функция системы имеет вид:

.

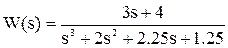Характеристическое уравнение: s³ + 2s² + 2.25s + 1.25 = 0.

Корни: s₁ = -1; s₂ = -0,5 + j; s₃ = -0,5 - j.

Следовательно, система устойчива. ¨

Критерий Стодолы.

Этот критерий является следствием из предыдущего и формулируется следующим образом: Линейная система устойчива, если все коэффициенты характеристического полинома положительны.

То есть, для передаточная из примера 3.1 по критерию Стодола соответствует устойчивой системе.

Критерий Гурвица.

Критерий Гурвица работает с характеристическим полиномом замкнутой системы. Как известно, структурная схема АСР по ошибке имеет вид (см. рис.)

W_p - передаточная функция регулятора,

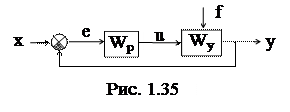W_y - передаточная функция объекта управления.

Определим передаточную функцию для прямой связи (передаточную функцию разомкнутой системы, см. п. 2.6.4): W_¥ = W_p W_y.

Далее с учетом наличия отрицательной обратной связи получаем передаточную функцию замкнутой системы:

.

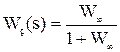Как правило, передаточная функция разомкнутой системы имеет дробно-рациональный вид:

.

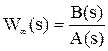Тогда после подстановки и преобразования получаем:

.

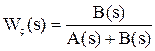Отсюда следует, что характеристический полином замкнутой системы (ХПЗС) можно определить как сумму числителя и знаменателя W_¥:

D_з(s) = A(s) + B(s).

Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с a_n+1 по a₀. Справа и слева от нее записываются коэффициенты с индексами через 2 (a₀, a₂, a₄… или a₁, a₃, a₅ …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля.

Если хотя бы один определитель будет равен нулю, то система будет находится на границе устойчивости.

Если хотя бы один определитель будет отрицателен, то система неустойчива не зависимо от числа положительных или нулевых определителей.

Пример.Дана передаточная функция разомкнутой системы

.

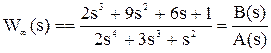Требуется определить устойчивость замкнутой системы по критерию Гурвица.

Для этого определяется ХПЗС:

D(s) = A(s) + B(s) = 2s⁴ + 3s³ + s² + 2s³ + 9s² + 6s + 1 = 2s⁴ + 5s³ + 10s² + 6s + 1.

Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а₄ = 2, а₃ = 5, а₂ = 10, а₁ = 6, а₀ = 1.

Матрица имеет вид:

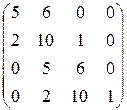
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:

Δ₁ = 5 > 0,

,

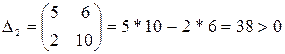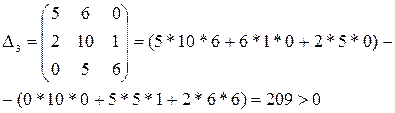
Δ₄ = 1* Δ₃ = 1*209 > 0.

Поскольку все определители положительны, то АСР устойчива. ♦

Критерий Михайлова.

Описанные выше критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, то есть может быть записана в виде

,

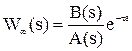где t - запаздывание.

В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно. Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.

Порядок применения критерия Михайлова:

1) Записывается характеристическое выражение замкнутой системы:

D_з(s) = A(s) + B(s)^.e^-ts.

2) Подставляется s = jw: D_з(jw) =Re(w) + Im(w).

3) Записывается уравнение годографа Михайлова D_з(jw) и строится кривая на комплексной плоскости.

Для устойчивой АСР необходимо и достаточно, чтобы годограф Михайлова (см. рис.), начинаясь при w = 0 на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании w от 0 до ¥ n квадрантов, где n - степень характеристического полинома.

Если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.

Критерий Найквиста.

Данный критерий аналогичен критерию Михайлова, но работает с АФХ системы, поэтому более сложен для расчетов.

Последовательность:

1) Определяется передаточная функция разомкнутой системы .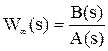

2) Определяется число правых корней m.

3) Подставляется s = jw: W_¥(jw).

4) Строится АФХ разомкнутой системы.

Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W_¥(jw) m раз охватывала точку (-1; 0), где m - число правых корней разомкнутой системы.

Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости.

В случае, если характеристическое уравнение разомкнутой системы A(s) = 0 корней не имеет (т.е. m = 0), то критерий, согласно критерию, замкнутая система является устойчивой, если АФХ разомкнутой системы W_¥(jw) не охватывала точку (-1; 0), в противном случае система будет неустойчива (или на границе устойчивости).

Показатели качества

Если исследуемая АСР устойчива, то может возникнуть вопрос о том, насколько качественно происходит регулирование в этой системе и удовлетворяет ли оно технологическим требованиям. На практике качество регулирования может быть определено визуально по графику переходной кривой, однако, имеются точные методы, дающие конкретные числовые значения.

Показатели качества разбиты на 4 группы:

1) прямые - определяемые непосредственно по кривой переходного процесса,

2) корневые - определяемые по корням характеристического полинома,

3) частотные - по частотным характеристикам,

4) интегральные - получаемые путем интегрирования функций.

Прямые показатели качества.

К ним относятся: степень затухания y, перерегулирование s, статическая ошибка е_ст, время регулирования t_p и др.

Рис. 1.38

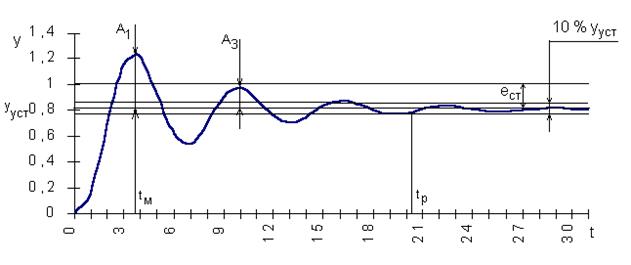Предположим, переходная кривая, снятая на объекте, имеет колебательный вид (см. рис. 1.38).

Сразу по ней определяется установившееся значение выходной величины у_уст.

Степень затухания y определяется по формуле

,

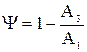где А₁ и А₃ - соответственно 1-я и 3-я амплитуды переходной кривой.

Перерегулирование s = 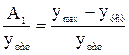, где y_max - максимум переходной кривой.

Статическая ошибка е_ст = х - у_уст, где х - входная величина.

Время достижения первого максимума t_м определяется по графику.

Время регулирования t_p определяется следующим образом: Находится допустимое отклонение D = 5% у_уст и строится «трубка» толщиной 2D. Время t_p соответствует последней точке пересечения y(t) с данной границей. То есть время, когда колебания регулируемой величины перестают превышать 5 % от установившегося значения.

Настройка регуляторов.

Типы регуляторов.

Для регулирования объектами управления, как правило, используют типовые регуляторы, названия которых соответствуют названиям типовых звеньев:

1) П-регулятор (пропорциональный регулятор)

W_П(s) = K₁.

Принцип действия заключается в том, что он вырабатывает управляющее воздействие на объект пропорционально величине ошибки (чем больше ошибка е, тем больше управляющее воздействие u).

2) И-регулятор (интегрирующий регулятор)

W_И(s) = .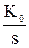

Управляющее воздействие пропорционально интегралу от ошибки.

3) Д-регулятор (дифференцирующий регулятор)

W_Д(s) = K₂ s.

Генерирует управляющее воздействие только при изменении регулируемой веричины:

u = K₂ .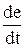

На практике данные простейшие регуляторы комбинируются в регуляторы вида:

4) ПИ-регулятор (пропорционально-интегральный регулятор)

W_ПИ(s) = K₁ + .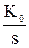

	Рис. 1.40

5) ПД-регулятор (пропорционально-дифференциальный регулятор)

W_ПД(s) = K₁ + K₂ s.

	Рис. 1.41

6) ПИД-регулятор.

W_ПИД(s) = K₁ + 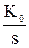+ K₂ s.

Наиболее часто используется ПИД-регулятор, поскольку он сочетает в себе достоинства