Определение геометрических размеров оси арок.

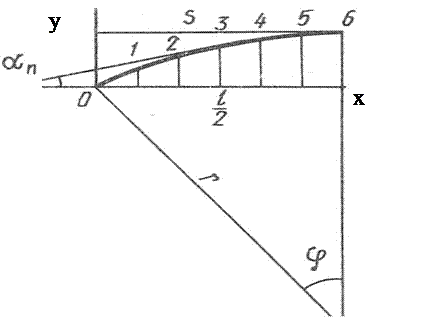
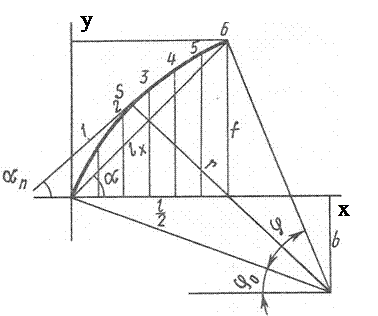
Геометрический расчет арки заключается в определении всех необходимых для статического расчета размеров углов наклона и их геометрических функций. Ввиду того, что арки имеют симмет­ричные схемы, такой расчет достаточно произвести только для одной, обычно левой половины схемы. Рассчитывать удобно в прямоугольной системе координат с началом в центре левого опор­ного узла (рис. 3.1). Основными исходными величинами являются ее пролет l и высота f, а в стрельчатой арке также радиус полуарок r.

а)

б)

Рис. 3.1. Геометрические схемы полуарок:

а – сегментной; б – стрельчатой.

Геометрический расчет треугольной арки заключается в опре­делении угла наклона оси арки a, длины оси полуарки s и коорди­нат сечений числом n, равных х и у, которые находятся из выражений:

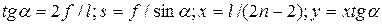
Геометрический расчет сегментной арки заключается в опреде­лении радиуса ее оси r, центрального угла дуги полуарки j, длины оси полуарки s, координат сечений х и у и углов наклона касательных an к оси в этих сечениях, которые определяются из выражений:

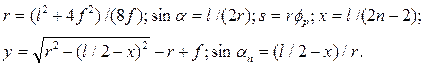
Геометрический расчет стрельчатой арки заключается в опре­делении следующих величин: угла наклона хорды a, длины хорды 1Х, центрального угла оси j, длины оси s, угла наклона первого радиуса j0, координат центра b и с, координат сечений x и у, координат сечений по хорде z, углов наклона касательных к оси an, расстояния ее от среднего радиуса до центра правой опоры. Эти величины определяются из следующих выражений:

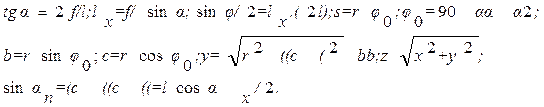
3.3. Сбор нагрузок на арки.

Нагрузки, приходящиеся на 1 м² горизонтальной поверхности, определяют от собственного веса арки и временной (снеговой и ветровой) нагрузок.

Сбор нагрузок производится согласно СНиП 2.01.07-85. «Нормы проектирования. Нагрузки и воздействия» и приложению 2 методических указаний по схеме, приведенной в табл. 3.1.

Таблица 3.1.

Наименование нагрузок	Нормативная	Коэффициент надежности по нагрузке gf	Расчетная
Кровля		1,2
Покрытие		1,1
Утеплитель		1,2
Арка		1,1
Итого	q		q
Снег по [2] п. 5.2, табл. 4
Ветер по [2] п. 6.4, табл.6
Всего	qн		qр

СНиП 2.01.07-85 прил.3

Номер схемы	Профили покрытий и схемы снеговых нагрузок	Коэффициенты m и область применения схем
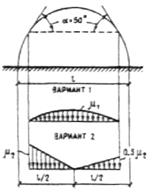	Здания со сводчатыми и близкими к ним по очертанию покрытиями	m1=l/8f, но не более 1.0 и не менее 0.4. Вариант 2 следует учитывать при f/l≥1/8: f/l 1/8 1/6 ≥1/5 m2 1.6 2.0 2.2 m1 = cos 1,8a; m2 = 2,4 sin 1,4a, где a — уклон покрытия, град

СНиП 2.01.07-85 прил.4

Номер схемы	Схемы зданий, сооружений, элементов конструкций и ветровых нагрузок	Определение аэродинамических коэффициентов с
	Здания со сводчатыми и близким к ним по очертанию покрытиями	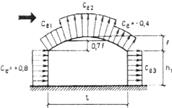Коэффициент h1/l Значения се1, се2 при f/l, равном 0,1 0,2 0,3 0,4 0,5 се1 +0,1 +0,2 +0,4 +0,6 0,7 0,2 -0,2 -0,1 +0,2 +0,5 +0,7 ≥1 -0,8 -0,7 -0,3 +0,3 +0,7 се2 Произ-ое -0,8 -0,9 -1 -1,1 -1,2

Статический расчет арок.

Производим в следующем порядке. Определяем действующие на арку расчетные нагрузки. Затем вычисляют опорные реакции — вертикальную R и горизонтальную H — и действующие в сечениях арки усилия — изгибающие моменты М, продольные N и поперечные Q силы. Затем подбирают сечения арки — ее верхнего и нижнего поясов и проверяют действующие в них нормальные s и скалывающие t напряжения, которые не должны превышать расчетных сопротив­лений древесины при сжатии R_c, растяжении R_р, скалывании t и расчетного сопротивления стали R. В заключение рассчитывают узловые соединения.

Распределенные нагрузки определяются с учетом шага расста­новки арок B. Они являются линейными и их удобно вычислять в кН/м, сосредоточенные нагрузки — в кН.

Постоянная нагрузка g условно, в небольшой запас прочности, считается равномерно распределенной по длине пролета арки, для чего ее фактическое значение увеличивается на отношение длины арки к ее пролету, т. е. 2S/l. Снеговая нагрузка S на треугольные и стрельчатые арки дается в нормах условно равномерно распре­деленной по длине пролета арки, расположенной на всем пролете или на полупролетах. Снеговая нагрузка на сегментные арки может быть равномерно распределенной по всему пролету или его половинам и зависит от отношения длины пролета к его высоте — l/(8f). Эта нагрузка S₁ может быть также треугольной с максимальными значениями над опорными узлами и нулевыми в коньке в зависимости от отношения высоты арки к пролету f/l.

Ветровая нагрузка W дается нормами равномерно распределен­ной по длине верхнего пояса арки. На пологие треугольные и сегментальные арки она действует в виде ветрового отсоса W и, как правило, не учитывается в расчете, так как она почти не увеличивает усилий, действующих в сечениях этих арок. На относительно высокие сегментные треугольные и стрельчатые арки ветровая нагрузка действует в виде давления W+ на подветренную сторону и отсоса W- на заветренную, обычно близких по значению. На стрельчатые арки ветровая нагрузка может приниматься условно равномерно распределенной по длине хорд полуарок. При расчете этих арок ветровая нагрузка обязательно учитывает­ся, так как она существенно увеличивает усилия в их сечениях. Сосредоточенные нагрузки от подвесного оборудования с грузами Р принимаются в соответствии с данными технологической части расчета.

Определение усилий в сечениях арок производится с учетом того, что трехшарнирные арки являются статически определенными конструкциями. Двухшарнирные арки однажды статически не определимы. Однако расчет их как трехшарнирных дает в большинстве случаев результаты, достаточно близкие к расчету, с учетом их статической неопределимости.

Опорные реакции трехшарнирной арки без затяжки, опираю­щиеся прямо на фундаменты, имеют вертикальные и горизон­тальные составляющие. Вертикальная опорная реакция арки R определяется из условия равенства нулю изгибающего момента в противоположном опорном шарнире. Горизонтальная опорная реак­ция Н, численно равная распору арки без затяжки, определяется из условия равенства нулю изгибающего момента в коньковом шарнире. В арке с затяжкой горизонтальная опорная реакция отсутствует. В такой арке возникает продольная растягивающая сила в затяжке, численно равная горизонтальной опорной реакции арки без затяжки. Например, при равномерной снеговой наг­рузке на левом полупролете арки без затяжки вертикальная опор­ная реакция левой опоры R = Зs1/8, а при этой нагрузке на правом полупролете R = s1/8. В обоих случаях горизонтальная опорная реакция H = 5sl2/(16f).

При треугольной снеговой нагрузке s₁ на левом полупролете арки с максимальным значением на опоре вертикальная опорная реакция левой опоры R = 5s₁l/24. При такой же нагрузке на правом полупролете вертикальная опорная реакция левой опоры R = sl/24. В обоих случаях горизонтальная опорная реакция H = sl²/(48f). Опорные реакции от двусторонней равномерной нагрузки будут равны сумме реакций от нагрузок на левом и правом полупролетах, т. е. R=q1/2 и H= ql²/(8f).

Усилия в сечениях арок — изгибающие моменты М, продоль­ные N и поперечные Q силы — определяются в зависимости от нагрузок, координат сечений x и у и углов наклона a, касательных к оси в этих сечениях. Например, при равномерной снеговой нагрузке s на левом полупролете арки М_х, Q_x и N_х определяются по формулам:

М_х = R_х — Ну — sх²/2; N_х = (R — sх)sina + Нcosa;

Q_х = (R — sx)соsa — Hsina.

При равномерной снеговой нагрузке на правой полуарке эти усилия определяются по тем же формулам без членов, содержа­щих нагрузку s. При треугольной нагрузке на левом полупролете с максимальным значением над опорой s₁ и промежуточными значе­ниями s_x= (1 — 2x/l)s₁ усилия в верхнем поясе сегментной арки определяются по формулам:

М_х = R_х — Ну — s₁х²/2+sx³/(3l); N_х = (R — s₁х+ s₁х²/l)sina + Нcosa;

Q_Х = (R— s₁x+ s₁х²/l)соsa — Hsina.

При треугольной снеговой нагрузке на правом полупролете усилия в левой полуарке сегментной арки определяют по этим же формулам без членов, содержащих нагрузку s₁.

Определение опорных реакций и усилий в сечениях удобно производить в одной, например, левой полуарке в следующем порядке. Сначала от снеговой равномерно распределенной и тре­угольной нагрузки на левом и затем на правом полупролете арки, затем от ветровой нагрузки при ветре слева и справа и далее от подвесного оборудования.

Изгибающие моменты следует определять во всех сечениях левой полуарки и иллюстрировать их эпюрами моментов. Продольные и поперечные силы можно определять только в опорном и коньковом шарнирах сегментных арок, где они достигают наибольших значений. Усилия от двусторонней снеговой равномерно распределенной нагрузки определяются путем суммирования усилий от снеговых нагрузок на левом и правом полупролетах арки, а усилия от постоянной равномерно распределенной нагрузки определяются путем умножения усилий от равномерно распределенной нагрузки на всем пролете арки на отношение постоянной и снеговой равномерно распределенных нагрузок g/s. Полученные значения сводятся в таблицу усилий в сечениях арки. Затем с помощью этой таблицы определяют мак­симальные положительные и отрицательные изгибающие момен­ты, продольные и поперечные силы в сечениях арки и опорные реакции при расчетных сочетаниях действующих нагрузок. При этом усилия от двух и более временных нагрузок уменьша­ются коэффициентом сочетаний k = 0,9.

Подбор сечения.

Подбор сечений деревянных арок производится на действие в них максимальных усилий — изгибающих моментов М, про­дольных N и поперечных Q сил, при наиболее неблагоприятных сочетаниях расчетных нагрузок.

Верхние пояса арок рассчитываются на сжатие с изгибом и скалывание, а нижние пояса — на растяжение.

Подбор сечения верхнего пояса клеедеревянной арки производится в следующем порядке: задаемся шириной прямоугольного сечения b в соответствии с шириной досок сортамента пиломатериалов и с учетом их острожки по кромкам. Определяем требуемый момент сопротивления W_тп и требуемую высоту сечения h_тр, исходя из формулы изгиба, в кото­рой влияние продольной силы можно учитывать коэффициентом 0,8:

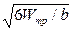
W_тр = М/(0,8R_и); h_тр =

Затем высоту сечения следует увязать с толщиной досок d, из которых склеивается арка после их острожки.

Проверка напряжений.

Проверка нормальных сжимающих напряжений в сечениях арки производится по формуле:

s=N/A+M_Д/W≤Rc,

где М_Д=М/x; x=1-N/(jR_cA).

Расчетное сопротивление сжатию должно приниматься с учетом высоты сечения m_б, ветра m_п, и толщины досок m_сл.

Проверка скалывающих напряжений производится в концах полуарки по формуле:

t=QS/(Ib)≤R_ск.

Расчет на устойчивость.

Расчет на устойчивость плоской формы деформи­рования верхнего пояса особенно необходим при расчете клеедеревянных арок, которые имеют сечения пояса значительной высо­ты h при относительно малой его ширине b. Этот расчет должен исключать опасность выхода пояса из вертикальной плоскости до момента потери им несущей способности по прочности. Верх­ние пояса арок закрепляются от выхода из вертикальной плоскости скатными связями в точках, равные расстояния между которыми называются расчетными длинами l_р. Эти связи, как правило, располагаются близ верхних кромок арок.

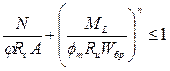
Расчетной длиной полуарки из ее плоскости является длина ее оси s.

Если условие не соблюдается, шаг скатных связей должен быть уменьшен или необходимы дополнительные связи, закрепляющие из плоскости нижнюю зону полуарки.