Волноводные многополюсники и их матрицы рассеяния

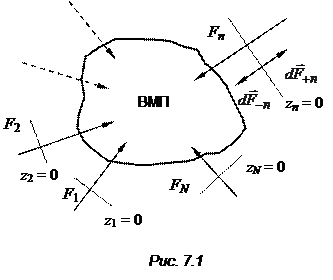
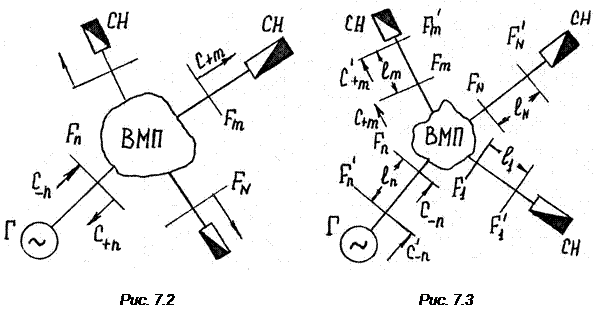
1. Волноводным многополюсником (ВМП) называется любое устройство, имеющее N входов в виде отрезков линий передачи (рис. 7.1). При этом во входных линиях введены отсчетные плоскости (сечения) 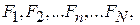которые являются условными границами ВМП и от которых отсчитывается продольная координата 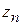, возрастающая в направлении ВМП (см. рис. 7.1). Поля волн, падающих на многополюсник 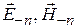и рассеянных многополюсником 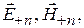представляются единообразно в виде произведения эталонных волн 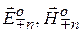и безразмерных комплексных амплитуд (коэффициентов)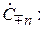

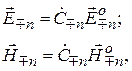(7.1)

где 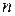– номер входа.

Под эталонными волнами понимаются падающие и волны, несущие одинаковую фиксированную мощность для всех N плеч:

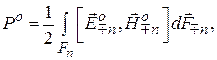(7.2)

где 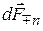– элемент поверхности поперечного сечения n-й линии передачи, направленный в сторону переноса мощности (см. рис. 7.1). В качестве эталонных волн могут быть использованы волны нормированных собственных функций. После выбора эталонных волн входных линий и соблюдения условий (7.1), (7.2) состояние ВМП по всем входам можно описывать безразмерными амплитудами падающих и расходящихся волн 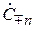в каждой из N линий.

2. Реакция ВМП на внешнее воздействие; матрицы рассеяния. Соотношения между амплитудами падающих и расходящихся волн (7.1) могут быть записаны в виде произведения матриц:

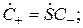(7.3)

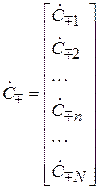(7.4)

– матрицы-столбцы амплитуд сходящихся («воздействие») 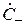расходящихся («реакция») 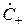волн;

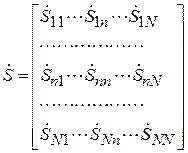(7.5)

– матрица рассеяния многополюсника.

Согласно формулам (7.3)–(7.5) амплитуду расходящейся волны, например в m-линии, можно записать:

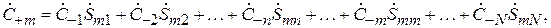(7.6)

где 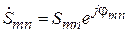– элементы матрицы рассеяния, безразмерные комплексные числа, характеризующиеся двумя числами: модулем 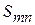и фазой 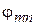. Если в (7.3) или в (7.6) положить все амплитуды сходящихся волн равными нулю, кроме одной 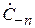, то становится ясным физический смысл каждого 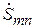как коэффициента прохождения или комплексного коэффициента передачи из 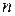-линии в 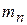-линию (рис. 7.2):

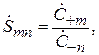(7.7)

Диагональный коэффициент 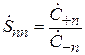имеет смысл комплексного коэффициента отражения в 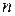-линии при условии, что все другие нагружены на согласованные нагрузки (СН) и все 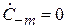(см. рис. 7.2):

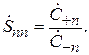(7.8)

3. Пересчет элементов S-матрицы при переносе отсчетных плоскостей. Допустим, имеется ВМП, у которого зафиксировано положение отсчетных плоскостей 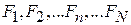и известны элементы S-матрицы, определенные (7.6) – (7.8). Перенесем отсчетные плоскости в направлении от ВМП на расстояние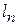 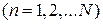. Возникнут новые отсчетные плоскости 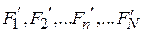(рис. 7.3). В этих сечениях комплексные амплитуды расходящихся волн (7.4) получат дополнительную фазовую задержку на величину 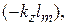а сходящиеся волны (7.4) получат опережение по фазе на величину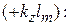

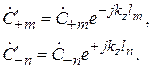(7.9)

Подставляя (7.9) в (7.8), найдем новое значение элементов новой 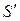-матрицы:

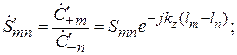(7.10)

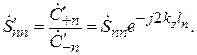(7.11)

4. Взаимные многополюсники. Большинство многополюсников обладают свойством взаимности: в таких ВМП коэффициент прохождения из 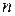-линии в 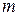-линию равен коэффициенту прохождения в обратном направлении из 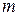-линии в 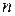-линию:

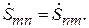(7.12)

Условие (7.12) есть условие взаимности матрицы S: коэффициенты, расположенные симметрично относительно главной диагонали (7.5), равны друг другу. Условие взаимности (7.12) могут нарушить ферритовые вкладыши в СВЧ-узлах, например ферритовые вентили или ферритовые циркуляторы.

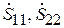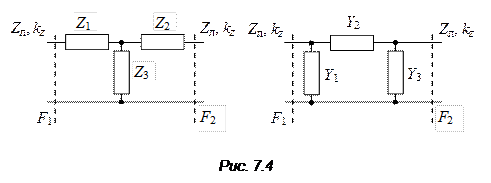
5. Канонические эквивалентные схемы волновых четырехполюсников (2N = 4). Поскольку S-матрица взаимного четырехполюсника (ЧП) содержит только три независимых элемента: и 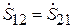(см. (7.12)), то минимальное число независимых элементов его эквивалентной схемы также должно быть равно трем. Это дает возможность в качестве схемной модели ЧП использовать Т-образные и П-образные схемы (рис. 7.4). Сопоставив матрицы рассеяния этих схем и взаимного ЧП, можно определить параметры схем:

для Т-схемы:

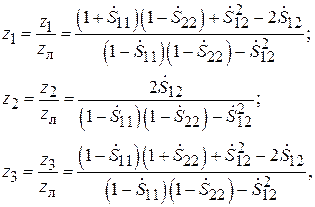(7.13)

для П-схемы:

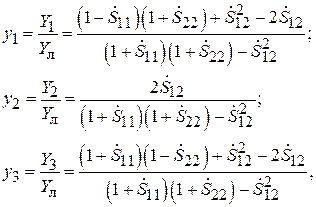(7.14)

7. S-матрица и эквивалентная схема симметричного волноводного ЧП. Электрически симметричными называют четырехполюсники, которые ведут себя одинаково при прямом и обратном включении. Таким образом, в матрице рассеяния ЧП

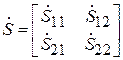(7.15)

имеются следующие дополнительные связи между элементами:

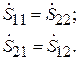(7.16)

Из (7.16) следует, что электрически симметричный ЧП всегда взаимен (см. (7.12)), но не наоборот. Эквивалентные схемы имеют два независимых элемента:

для Т-схемы:

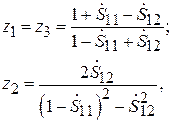(7.17)

для П-схемы:

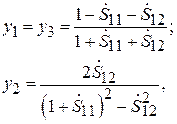(7.18)

7. S-матрицы симметричных ЧП с поперечными неоднородностями и их эквивалентные схемы. Поперечными неоднородностями называются такие неоднородности, размеры которых вдоль оси линии очень малы. Они подразделяются да симметрично и антисимметрично рассеивающие. К симметрично рассеивающим относятся: индуктивная и емкостная диафрагма в волноводе, индуктивный или емкостный штыри в волноводе, диск на внутреннем проводнике коаксиала (рис. 7.5) и др. Примерами антисимметрично рассеивающих четырехполюсников являются: поперечный разрез внутреннего проводника коаксиала, поперечная узкая щель в широкой стен

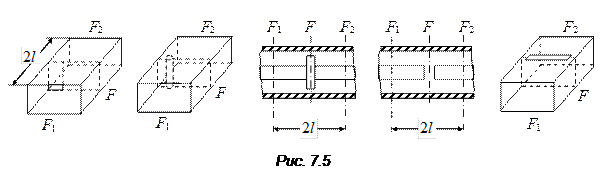ке волновода. Эти неоднородности геометрически и электрически симметричны, и поэтому их S-матрицы определяются согласно (7.15) и (7.16). Малая протяженность этих неоднородностей позволяет найти дополнительные связи между элементами матрицы рассеяния 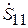, 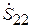и уменьшить общее число независимых элементов, определяющих их матрицу и эквивалентную схему. Если выбрать отсчетные плоскост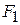и и 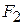на равных расстояниях 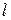от неоднородности, находящейся в плоскости 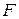(рис. 7.6, 7.7), то можно показать, что недиагональные элементы матрицы рассеяния определяются следующим образом:

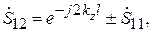(7.19)

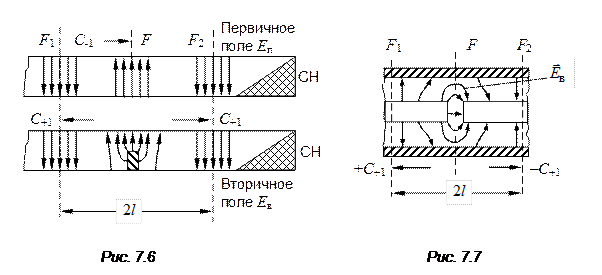
где 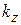– продольное волновое число в линии. Двойной знак «±» перед 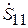в (7.19) соответствует симметрично и антисимметрично рассеивающим неоднородностям.

На рис. 7.6, 7.7 изображены картины силовых линий электрических полей, созданных штырем в волноводе и разрывом внутреннего проводника коаксиала, при падении на них волны основного типа.

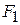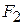Если отсчетные плоскости перенести из и в плоскость 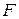(в направлении к ЧП!), то, согласно формулам (7.10), (7.11), новая матрица рассеяния примет вид

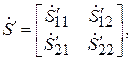(7.20)

где

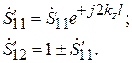(7.21)

Подстановка (7.20). (7.21) в (7.17), (7.18) значительно упрощает эквивалентные схемы ЧП:

для П-схемы

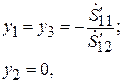(7.22)

для Т-схемы

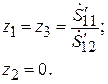(7.23)

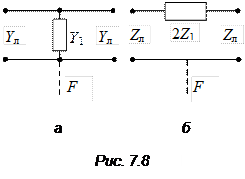
Согласно (7.22), эквивалентная схема симметрично рассеивающей неоднородности содержит только один элемент – поперечную проводимость (рис. 7. 8, а):

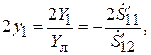(7.24)

Согласно (7.23), эквивалентная схема антисимметрично рассеивающей неоднородности содержит только один элемент – последовательное сопротивление (рис. 7.8, б):

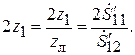(7.25)

8. S-матрицы и эквивалентные схемы реактивных ЧП. Реактивный многополюсник удовлетворяет следующим требованиям: а) в нем отсутствуют потери мощности; б) энергетический обмен с внешним пространством происходит только по входным линиям.

Мощность, входящая в многополюсник по входным линиям, равна мощности, выходящей через те же линии. Матрица рассеяния реактивного многополюсника обладает свойством унитарности:

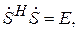(7.26)

где 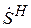– матрица, эрмитово-сопряженная к S (т. е. матрица S, к которой применены операций транспонирования и комплексного сопряжения: 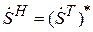); S – матрица рассеяния; 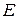– единичная матрица. Факт унитарности S-матрицы (7.26) означает, что между ее элементами имеются связи, которые придают ей специфический вид. S-матрица реактивного четырехполюсника приобретает следующую структуру:

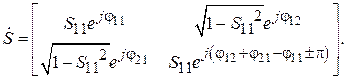(7.27)

Из (7.27) видно, что для определения матрицы необходимо знать четыре вещественные числа: 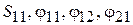. Эквивалентные схемы реактивных четырехполюсников состоят из реактивных (не поглощающих) элементов.

9. S-матрицы и эквивалентные схемы реактивных четырехполюсников с поперечными неоднородностями. Четырехполюсники с поперечными неоднородностями имеют матрицы рассеяния, определяемые соотношениями (7.19), и одновременно структуру типа (7.27), так как четырехполюсники реактивные. Использование соотношения (7.19) для S-матрицы (7.27) позволяет получить матрицу S реактивной поперечной неоднородности:

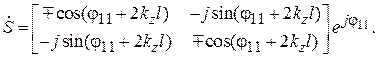(7.28)

Из (7.28) видно, что для записи S-матрицы нужно знать: фазу диагонального элемента 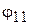и электрическую длину 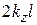между отсчетными плоскостями F₁ и F₂. При переносе отсчетных плоскостей в плоскость неоднородности F все элементы S-матрицы (7.28) Нужно домножить на экспоненту 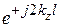. Новая матрица S примет вид:

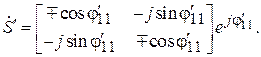(7.29)

Из (7.29) видно, что матрицу S можно записать, зная только фазу ее диагонального элемента и тип четырехполюсника симметрично «–» или антисимметрично «+» рассеивающий.

Подставляя в формулы (7.24) или (7.25) значения 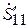и 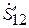, из (7.29) находим для обоих типов неоднородностей реактивные элементы эквивалентных схем (см. рис. 7.8):

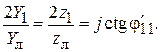(7.30)

Типичными представителями реактивных ЧП с поперечными неоднородностями являются диафрагмы и штыри в волноводах, диск на внутреннем проводнике коаксиала. Эти ЧП относятся к типу симметрично рассеивающих. Четырехполюсник в виде разреза внутреннего проводника коаксиала – реактивный антисимметрично рассеивающий.

7.2. Экспериментальное определение элементов S-матриц
четырехполюсников с поперечной неоднородностью

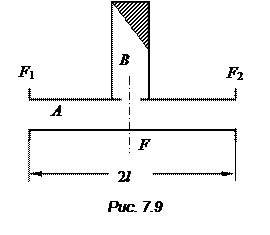1. Антисимметрично рассеивающий (АСР) четырехполюсник с потерями. Волновой ЧП с потерями (рис. 7.9) состоит из двух волноводов А и В; в широкой стенке волновода А прорезана узкая поперечная щель, связывающая его с волноводом В, в котором имеется поглотитель. Так как поперечная щель является антисимметрично рассеивающей неоднородностью, то ее матрица S, отнесенная к плоскостям 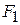, , 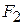имеет вид (7.19). При определении ее элементов достаточно найти модуль 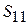и фазу 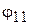диагонального элемента и электрическую длину ЧП 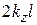. Для этого необходимо измерить геометрическую длину ЧП 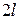и определить длину волны в волноводе А, тогда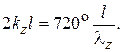

При определении 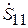необходимо пользоваться методикой измерения коэффициента отражения, изложенной в 1–3, а именно, подключить к концу ИЛ короткозамыкатель (КЗ), измерить координаты двух соседних условных конца 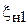, 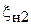и определить длину волны 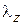. Затем вместо КЗ подключается ЧП, нагруженный на втором входе на согласованную нагрузку (СН); измеряется КБВ и 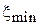. Находится модуль 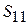и смещение минимума 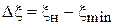и определяется фаза 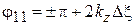. Для определения 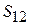= 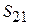необходимо воспользоваться (7.19). Пересчет S-матрицы к плоскости F осуществляется умножением ее элементов на 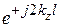. Эквивалентная схема, соответствующая совмещенным плоскостям отсчета, представляется последовательным сопротивлением (см. рис. 7.8, б), которое рассчитывается по (7.25).

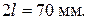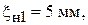
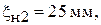
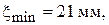
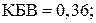
Рассмотрим пример расчета параметров антисимметрично рассеивающего ЧП с потерями, длиной Результаты эксперимента: 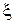возрастает от нагрузки к генератору. Результаты расчета приведены в табл. 7.1.

Таблица 7.1

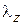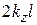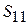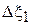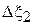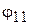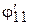	630o	0,47		-4	108o	18o

Комплексные величины S-параметров и эквивалентного сопротивления:

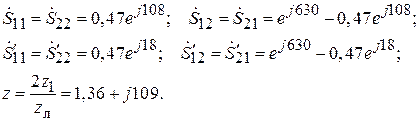
2. Реактивный сильно отражающий симметрично рассеивающий ЧП с поперечной неоднородностью. Этот ЧП имеет структуру S-матрицы типа (7.28) с верхним знаком. Из (7.28) видно, что для нахождения S-матрицы необходимо определить фазовый угол 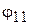элемента 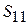и электрическую длину ЧП 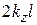. В отличие от п.1 здесь можно опустить измерение КБВ, а модул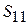и и 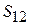вычислять по (7.28). Формулы (7.29, а), (7.30) определяют эквивалентную проводимость ЧП.

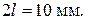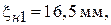
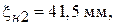
Рассмотрим пример расчета параметров реактивного сильно отражающего симметрично рассеивающего ЧП длиной Результаты эксперимента: 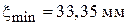; 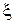возрастает от нагрузки к генератору.

Результаты расчета приведены в табл. 7.2.

Таблица 7.2

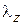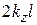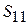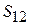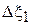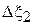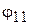	72o	0,707	0,707	16,65	-8,15	135o	18o

S-параметры и эквивалентная проводимость:

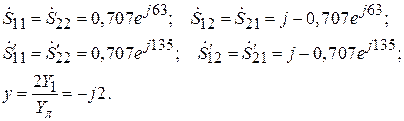
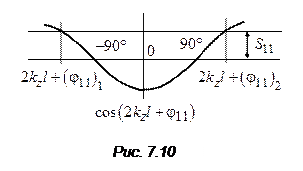Изложенный метод дает приемлемую точность, если коэффициент отражения достаточно высок ( 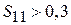), минимумы достаточно глубоки и их местоположения 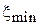определяются сравнительно точно. В случае слабо отражающих ЧП ( 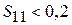) минимумы будут неглубоки (не «остры»), и их положения 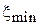определить с большой точностью не удается, что приводит к ошибкам при вычислениях.

3. Реактивный слабо отражающий ЧП с поперечной неоднородностью. Слабо отражающими ЧП являются, например диафрагмы с большим размером окна и штыри, сильно смещенные к узкой стенке волновода. Набор измеряемых величин тот же, что и в п. 1.

Значение КБВ, близкое к единице, измеряется достаточно точно, а положение минимума 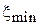измеряется с погрешностью, и поэтому неточно определяется фаза коэффициента отражения 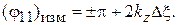Для уточнения 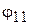используются (7.28), (3.42):

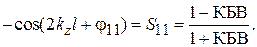(7.31)

Из уравнения (7.31) находятся два решения для 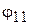(рис. 7.11):

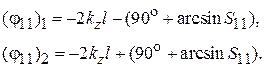
Из двух решени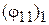й и 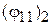выбирается то, которое ближе к измеренному 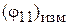. Далее расчет, как в п. 2.

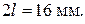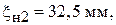
Рассмотрим пример расчета параметров реактивного слабо отражающего ЧП длиной Результаты эксперимента: 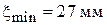(определен с ошибкой); 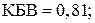возрастает от нагрузки к генератору. Результаты расчета приведены в табл. 7.3.

Таблица 7.3

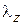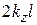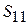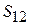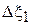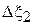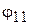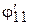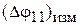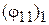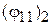	128o	0,105	0,996		–5,5	–224o	–96o	92o	–224o	–32o

Уточненное значение 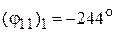(или +136°) – это то, которое ближе к 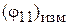(рис. 7.11).

S-параметры и эквивалентная проводимость:

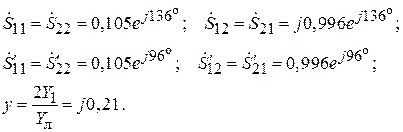
Порядок выполнения работы

1. Определение местоположения условных концов ИЛ и длины волны в волноводе. Закоротите ИЛ. Найдите отсчеты условных концов 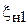, 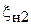и длину волны на частоте в пределах частотного диапазона генератора.

2. Определение элементов матрицы рассеяния и эквивалентной схемы антисимметрично рассеивающего четырехполюсника с потерями. Подключите к концу ИЛ четырехполюсник (рис. 7.9). К второму входу ЧП подключите СН. Определите КБВ и местоположение минимума между условными концами. Измерьте геометрическую длину четырехполюсника 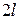. По этим данным рассчитайте: элементы матрицы рассеяния S для отсчетных плоскостей, разнесенных на 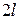, элементы матрицы рассеяния S' и значение нормированного последовательного сопротивления 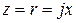эквивалентной схемы для отсчетных плоскостей, совмещенных с плоскостью симметрии ЧП. В отчете необходимо воспроизвести все этапы расчета этих величин по образцу задачи из п. 1.

3. Определение элементов S-матрицы и эквивалентной схемы реактивного симметрично рассеивающего сильно отражающего ЧП.

Подключите к концу ИЛ четырехполюсник в виде отрезка волновода с диафрагмой или поперечным штырем (штырями). Должен быть взят заведомо сильно отражающий ЧП. Ко второму входу ЧП долина быть подключена согласованная нагрузка. Определите местоположение минимума 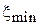между условными концами ИЛ. Измерьте геометрическую длину ЧП 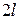. По этим данным рассчитайте: элементы матрицы рассеяния S для отсчетных плоскостей, разнесенных на 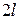, элементы матрицы рассеяния S' и значение нормированной параллельной проводимости 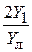эквивалентной схемы для отсчетных плоскостей, совмещенных с плоскостью симметрии ЧП. В отчете необходимо воспроизвести все этапы расчета этих величин по образцу задачи из п. 2.

4. Определение элементов матрицы рассеяния и эквивалентной схемы реактивного симметрично рассеивающего слабо отражающего ЧП.

Подключите к концу ИЛ четырехполюсник, в виде отрезка волновода с диафрагмой или поперечным штырем. Должен быть взят заведомо слабо отражающий ЧП. Ко второму входу ЧП подключите СН. Определите местоположение минимума между условными концами ИЛ. Измерьте геометрическую длину ЧП 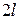. По этим данным рассчитайте: элементы матрицы рассеяния для отсчетных плоскостей, разнесенных на 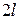; элементы матрицы рассеяния S' и значение нормированной параллельной проводимости 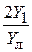эквивалентной схемы для отсчетных плоскостей, совмещенных с плоскостью симметрии ЧП. В отчете необходимо воспроизвести все этапы расчета этих величин по образцу задачи из п. 3, в том числе привести эскизы типа рис. 7.10, 7.11.

5. По каждому этапу расчета должны быть приведены формулы, исходные числа, размерности величин.

7.4. Контрольные вопросы

1. Что является волноводным многополюсником?

2. Как определяются границы ВМП?

3. Что такое эталонные волны и зачем они нужны?

4. Что такое матрица рассеяния ВМП?

5. Какой физический смысл элементов матрицы рассеяния?

6. Как изменяются элементы матрицы рассеяния при переносе отсчетных плоскостей?

7. Что такое взаимные ВМП и каковы их свойства?

8. Каково условие взаимности ВМП?

9. Вывести формулы для сопротивлений эквивалентной Т-схемы через элементы матрицы рассеяния четырехполюсника.

10. Вывести формулы для проводимостей эквивалентной П-схемы через элементы матрицы рассеяния четырехполюсника.

11. Какова матрица рассеяния симметричного четырехполюсника и каковы их эквивалентные схемы?

12. Что является поперечными неоднородностями и каковы их матрицы рассеяния и эквивалентные схемы?

13. В чем различия симметричного и антисимметричного рассеивающих поперечных неоднородностей?

14. Какова матрица рассеяния симметричного и антисимметричного рассеивающих поперечных неоднородностей?

15. Какова матрица рассеяния и эквивалентные схемы симметричного и антисимметричного рассеивающих поперечных неоднородностей?

16. Что называется реактивными ВМП?

17. Что означает эрмитово-сопряженная матрица?

18. Что означает свойство унитарности реактивного ВМП?

19. Какова структура матрицы рассеяния реактивного четырехполюсника?

20. Какова структура матрицы рассеяния симметричного и реактивного четырехполюсника?

21. Как зная фазу коэффициента отражения симметричного и реактивного четырехполюсника, можно определить матрицу рассеяния и эквивалентную схему?