Проблема согласования нагрузки с линией передачи
Нагрузка, подключенная к концу линии передачи, называется согласованной, если её нормированное сопротивление или проводимость равны единице: 
В линии устанавливается режим бегущей волны. На практике возникают ситуации, когда условие 
не выполняется и в то же время линию и нагрузку изменять запрещено. В этих условиях необходимо изыскать способ обеспечения в линии режима бегущей волны, причем вся мощность этой волны должна поглощаться в нагрузке.
Общий принцип, который кладется в основу при решении этой проблемы, состоит в том, что нагрузка подключается к линии не непосредственно, а через согласующий трансформатор (рис. 6.5, а).
От трансформатора требуется, чтобы он трансформировал проводимость 
подключенную к его выходным клеммам, в проводимость, равную единице на его входных клеммах:
(6.10)
Это есть условие согласования, при котором в линии устанавливается режим бегущей волны. Поскольку отраженной волны нет, а в трансформаторе потери должны отсутствовать, вся мощность падающей волны поглощается в нагрузке.
Трансформаторы, применяемые на СВЧ, выполняются на отрезках линий. Рассмотрим устройство трансформа-тора, реализующего так называемое одношлейфное согласование (рис. 6.5, б). Трансформатор представляет собой отрезок линии длиной 
, на входе которого включена параллельная реактивная неоднородность, имеющая нормированную проводимость 
. Полная проводимость на входе трансформатора складывается из двух параллельно включенных проводимостей: проводимости и проводимости 
Эта вторая проводимость представляет собой проводимость нагрузки, трансформированную к входным клеммам отрезком линии длиной . Итак:
(6.11)
Подстановка (6.10) в (6.11) дает условие согласования в виде двух равенств:
(6.12)
(6.13)
Условие (6.12) можно удовлетворить путем выбора такой относительной длины трансформирующего отрезка 
чтобы активная часть проводимости 
была равна единице: 
Условие (6.13) можно удовлетворить подбором реактивной проводимости (проводимости шлейфа): 
; 
Приведём пример расчета.
Задача. Проводимость нагрузки 
Длина волны в линии 
Рассчитайте длину трансформирующей секции и реактивную проводимость 
, при которых в основной обеспечивается режим бегущей волны.
Решение. Нанесем на диаграмму проводимостей точку 1, соответствующую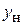 
(рис. 6.6). Отсчет по шкале «к генератору», соответствующий этой точке, равен 0,222, а КБВ = 0,23. Перемещаясь по окружности КБВ = 0,23 к генератору, непременно доходим до точки 2, через которую проходит окружность 
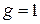. Отсчет по шкале перемещений, соответствующий точке 2, равен 0,32, а значение реактивной проводимости здесь 
Таким образом, на расстоянии 
от нагрузки трансформированная проводимость 
Чтобы компенсировать реактивную проводимость 
, проводимость шлейфа нужно выбрать равной 
Итак, длина трансформирующего отрезка 
Если линия передачи – волновод, то в качестве шлейфа можно взять емкостную диафрагму, подобрав ее ширину по формуле (6.9).
Из рис. 6.6 видно, что имеется другой вариант трансформатора: в точке 2' на круговой диаграмме проводимость , так же, как и в точке 2, имеет активную часть, равную единице. В этом случае реактивный шлейф должен иметь индуктивную проводимость, а длина отрезка 
должна быть больше, чем в рассчитанном случае.
Порядок выполнения работы
1. Нахождение условных концов линии и длины волны в волноводе. Установите частоту генератора, заданную преподавателем. Подключите к концу ИЛ заглушку и определите положение двух соседних условных концов линии. Определите длину волны в волноводе и сравните ее с расчетным значением, найденным по формуле (3.19).
2. Определение входной проводимости подвижной нагрузки. Подключите к концу ИЛ подвижную нагрузку и установите перемещаемый клин в какое-нибудь фиксированное положение (начальный отсчет по шкале нагрузки 
должен быть не очень велик – не более 10...15 мм). Измерьте нормированную проводимость нагрузки, отнесенную к ее входному фланцу. Методика измерений по 4.8, но с учетом того, что измеряется проводимость, а не сопротивление. Приведите эскиз (типа рис. 1.6). Рассчитайте относительные расстояния 
и 
. Пользуясь круговой диаграммой, определите 
и 
. В отчете необходимо поместить рисунок (типа рис. 4.7) с указанием всех числовых данных, получаемых при построении на круговой диаграмме. Точка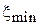 
должна быть на нижней полуоси диаграммы проводимостей.
3. Расчет одношлейфного согласования. Дальнейшей задачей является одношлейфное согласование подвижной нагрузки с проводимостью 
, определенной в 6.2. По методике 6.6 рассчитайте минимальную длину трансформирующего отрезка и проводимость реактивного шлейфа . Определите, какую диафрагму (индуктивную или емкостную) нужно включить в качестве шлейфа, и по (6.8) или (6.9) найдите размер окна диафрагмы С. В отчете приведите полный расчет согласующего трансформатора по схеме задачи из 6.6 (иллюстрация типа рис. 6.6 обязательна).
4. Проверка качества согласования. Из имеющегося набора выберите диафрагму с нужным Вам размером окна С. Разместить ее можно только в плоскости выходного фланца ИЛ. Соберите схему рис. 6.7. Если Вы оставите отсчет по шкале нагрузки равным , то расстояние между диафрагмой и нагрузкой будет равно нулю, тогда как оно должно быть равно . Поэтому сместите перемещенный клин на от диафрагмы. Тогда отсчет по шкале нагрузки должен быть ( + ). Измерьте КБВ в ИЛ. Он должен оказаться существенно ближе к единице, чем в п. 2. Идеального согласования может и не получиться, поскольку диафрагма рассчитывалась по приближенной формуле. Поэтому попытайтесь путем небольших смещений нагрузки повысить КБВ в ИЛ (скорректированный КБВ).
5. Частотная зависимость согласования. Ничего не изменяя в узле «нагрузка – трансформатор» измерьте зависимость КБВ в ИЛ от частоты. Шаг по частоте 100...200 МГц. Количество частотных точек по 3–4 выше и ниже рабочей частоты. При изменении частоты не забывайте перестраивать резонатор ИЛ. Постройте график.
6.7. Контрольные вопросы
1. Как записываются напряжение и ток в виде волн через коэффициент отражения?
2. Какова связь коэффициента отражения и нагрузки?
3. Что такое входное сопротивление линии, и какова его формула?
4. Что такое входная проводимость линии, и какова ее формула?
5. Как меняется сопротивление (или проводимость) вдоль линии?
6. Каково сопротивление (или проводимость) в точках минимума и максимума напряжения и как оно связано с КБВ и КСВ?
7. В чем отличие и сходство круговых диаграмм сопротивлений и проводимостей?
8. Как вводятся понятия нормированных сопротивлений (или проводимостей) волноводов?
9. Что собой представляет продольная координата на круговой диаграмме сопротивлений (или проводимостей) для волноводов?
10. Как возникает вторичное (рассеянное) поле, отраженное от диафрагмы?
11. Как может быть представлена реактивная часть вторичного поля созданного диафрагмой? И какова его особенность?
12. Как представляется полное поле основного типа, распространяющиеся «за» диафрагмой?
13. Как пояснить, что «индуктивная» диафрагма является именно индуктивной, а «емкостная» – емкостной?
14. Покажите, как по круговой диаграмме найти входное сопротивление в сечении 2, если оно известно в сечении 1.
15. Как, зная нормированное сопротивление в некотором сечении линии, найти нормированную проводимость в том же сечении?
16. В чем состоит принцип одношлейфного согласования?
7. ИССЛЕДОВАНИЕ ВОЛНОВОДНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ
С ПОПЕРЕЧНЫМИ НЕОДНОРОДНОСТЯМИ
Цель работы: изучение свойств и измерение элементов матриц рассеяния волновых многополюсников.