Основные свойства и характеристики волн в ВС
1. Из курсов «Электромагнитные поля и волны» и «Техническая электродинамика» следует, что комплексные амплитуды вектора напряженности электрического 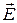 и магнитного полей
и магнитного полей 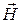 в волноводах, а также напряжения U, тока I в длинных линиях представляют собой суперпозицию прямых (падающих) и обратных (отраженных) волн:
в волноводах, а также напряжения U, тока I в длинных линиях представляют собой суперпозицию прямых (падающих) и обратных (отраженных) волн:
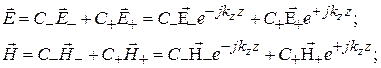 (1.1)
(1.1)
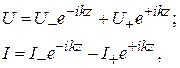 (1.2)
(1.2)
где 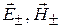 – собственные векторные функции основного типа поля волновода прямой «–» и обратной «+» волн;
– собственные векторные функции основного типа поля волновода прямой «–» и обратной «+» волн; 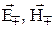 – векторные функции поперечных координат волновода;
– векторные функции поперечных координат волновода; 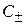 – комплексные амплитуды (безразмерные коэффициенты) прямой «–» и обратной «+» волн в волноводе;
– комплексные амплитуды (безразмерные коэффициенты) прямой «–» и обратной «+» волн в волноводе; 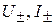 – комплексные амплитуды напряжения и тока прямой «–» и обратной «+» волн в длинной линии;
– комплексные амплитуды напряжения и тока прямой «–» и обратной «+» волн в длинной линии;
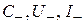 – определяются уровнем мощности генератора;
– определяются уровнем мощности генератора;
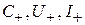 – определяются отражением волн от нагрузки;
– определяются отражением волн от нагрузки;
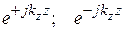 (1.3)
(1.3)
– множители, определяющие фазу колебаний прямой «–» и обратной «+» волн в поперечном сечении длинной линии или волновода с продольной координатой z; k – волновое число или фазовая постоянная свободного пространства (фазовая постоянная для длинной линии и свободного пространства совпадают), длина волны 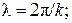
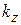 – продольное волновое число в волноводе для основного типа, длина волны
– продольное волновое число в волноводе для основного типа, длина волны 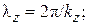
2. В результате наложения прямой и обратной волн в линиях и волноводах возникает интерференционная картина распределения модуля комплексной амплитуды суммарного поля вдоль оси волноведущей структуры: регулярно чередующиеся с периодом в половину длины волны максимумы и минимумы. На рис. 1.4 изображен один из возможных вариантов интерференционной картины.
3. Для характеристики уровня отражения вводится понятие коэффициента отражения от нагрузки 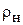 , как отношение комплексных амплитуд отраженной
, как отношение комплексных амплитуд отраженной 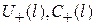 и падающей
и падающей 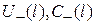 волн в месте подключения нагрузки (т. е. при
волн в месте подключения нагрузки (т. е. при 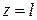 , где
, где 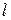 – длина линии или
– длина линии или 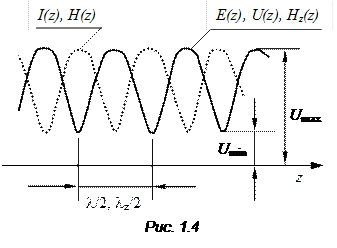 волновода):
волновода):
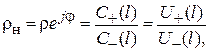 (1.4)
(1.4)
где 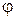 – фаза коэффициента отражения от нагрузки,
– фаза коэффициента отражения от нагрузки, 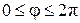 (или
(или 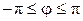 );
); 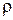 – модуль коэффициента отражения,
– модуль коэффициента отражения, 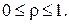
4. Полученные соотношения (1.1)–(1.4) позволяют представить распределение модуля амплитуды напряжения 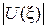 или напряженности электрического поля
или напряженности электрического поля 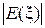 вдоль волноведущей структуры следующим образом:
вдоль волноведущей структуры следующим образом:
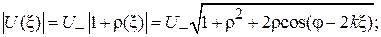 (1.5)
(1.5)
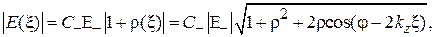 (1.6)
(1.6)
где 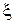 – координата вдоль линии (или волновода), отсчитываемая от конца (от нагрузки в сторону генератора);
– координата вдоль линии (или волновода), отсчитываемая от конца (от нагрузки в сторону генератора); 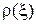 – коэффициент отражения в сечении волноведущей структуры с продольной координатой
– коэффициент отражения в сечении волноведущей структуры с продольной координатой 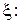
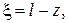 (1.7)
(1.7)
для линии
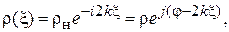 (1.8)
(1.8)
для волновода
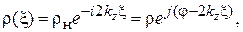 (1.9)
(1.9)
где 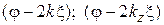 – полная фаза коэффициента отражения в сечении с координатой
– полная фаза коэффициента отражения в сечении с координатой 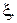
Из формул (1.5), (1,6), (1,8), (1,9) видно, что на расстояниях 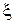 от конца линии (или волновода) кратных целому числу полуволн значение напряжения (или поля) равно значению напряжения (поля) на конце линии (волновода.) Эти значения
от конца линии (или волновода) кратных целому числу полуволн значение напряжения (или поля) равно значению напряжения (поля) на конце линии (волновода.) Эти значения 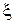 можно назвать условными концами линии (волновода).
можно назвать условными концами линии (волновода).
Условными концами называются координаты 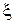 , отстоящие от реального конца линии (или волновода) на расстояниях кратных целому числу полуволн; обозначим их
, отстоящие от реального конца линии (или волновода) на расстояниях кратных целому числу полуволн; обозначим их 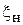 :
:
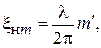
где 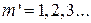 и т. д., тогда
и т. д., тогда
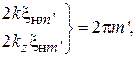
Из (1.8), (1.9) видно, что модуль коэффициента отражения постоянен вдоль волноведущей структуры, а фаза меняется по линейному закону (рис. 1.5, а).
В тех сечениях волноведущей структуры, где фаза принимает значения, кратные нечетному числу  , коэффициент отражения становится вещественным и отрицательным, прямая и обратная волны складываются в противофазе:
, коэффициент отражения становится вещественным и отрицательным, прямая и обратная волны складываются в противофазе:
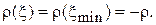 (1.10)
(1.10)
В этих сечениях наблюдается минимум электрического поля (или напряжения) (см. рис. 1.5, а):
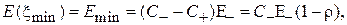 (1.11)
(1.11)
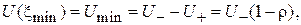 (1.12)
(1.12)
Местоположения минимумов 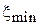 определяются из уравнений:
определяются из уравнений:
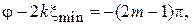 (1.13)
(1.13)
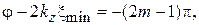 (1.14)
(1.14)
где m = 1, 2, 3,… – порядковый номер минимума, если его считать от конца линии, т. е. от нагрузки. В тех сечениях, где прямая и обратная волны складываются в фазе, наблюдается максимум (см. рис. 1.5, а):
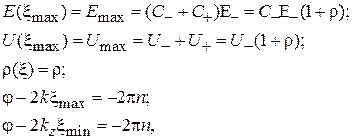 (1.15)
(1.15)
где n – целое число.
5. Для характеристики интерференционной картины в волноведущей структуре и для оценки степени согласования линии или волновода с нагрузкой вводятся понятия коэффициента бегущей волны (КБВ) и обратного ему коэффициента стоячей волны (КСВ):
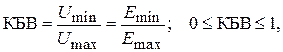 (1.16)
(1.16)
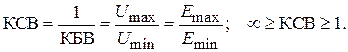 (1.17)
(1.17)
Используя формулы (1.10)–(1.17), легко вывести простые соотношения, связывающие КБВ, КСВ, модуль коэффициента отражения 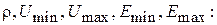
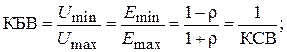 (1.18)
(1.18)
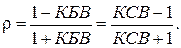 (1.19)
(1.19)
Формулы (1.18)–(1.19) являются расчетными формулами технических характеристик интерференционной картины в волноведущей структуре и степени согласования линии (волновода) с нагрузкой.
1.3. Экспериментальное определение коэффициента отражения
от исследуемой нагрузки
1. Коэффициент отражения от нагрузки является, как видно из (1.4), комплексной величиной 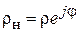 .
.
Для определения модуля 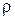 коэффициента отражения необходимо присоединить исследуемую нагрузку к концу линии (волновода), измерить КБВ (или КСВ) и затем вычислить
коэффициента отражения необходимо присоединить исследуемую нагрузку к концу линии (волновода), измерить КБВ (или КСВ) и затем вычислить 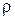 по формуле (1.19).
по формуле (1.19).
2. Для определения фазы φ коэффициента отражения от исследуемой нагрузки необходимо знать, согласно формулам (1.13), (1.14), расстояние от нагрузки до положения минимума. Как правило, в реальных устройствах СВЧ точно определить это расстояние практически невозможно. Поэтому для определения фазы φ коэффициента отражения от исследуемой нагрузки необходимо использовать эталонную нагрузку с заранее известной фазой коэффициента отражения φ', составив для нее уравнение, аналогичное уравнениям (1.13), (1.14):
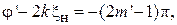 (1.20)
(1.20)
где 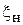 – положения минимума для эталонной нагрузки: m = 1, 2, 3,…
– положения минимума для эталонной нагрузки: m = 1, 2, 3,…
Почленно вычитая уравнение (1.20) из (1.13), легко получить:
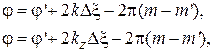 (1.21)
(1.21)
где
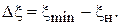
Слагаемое – 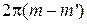 в формулах (1.21) можно в дальнейшем опустить, так как оно добавляет к значению фазы целое число (
в формулах (1.21) можно в дальнейшем опустить, так как оно добавляет к значению фазы целое число ( 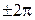 ) или нуль. Таким образом, для определения φ необходимо знать φ¢ и смещение положения минимума
) или нуль. Таким образом, для определения φ необходимо знать φ¢ и смещение положения минимума 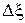 .
.
3. В качестве эталонной нагрузки используется короткозамыкающая перемычка (заглушка), для которой коэффициент отражения известен (см. п. 4):
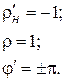 (1.22)
(1.22)
Подставляя (1.22) в уравнение (1.21), можно получить расчетную формулу для фазы коэффициента отражения от исследуемой нагрузки:
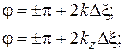 (1.23)
(1.23)
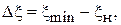 (1.24)
(1.24)
где 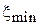 – положение минимума напряженности электрического поля в волноведущей структуре при установке на конец линии (волновода) исследуемой нагрузки;
– положение минимума напряженности электрического поля в волноведущей структуре при установке на конец линии (волновода) исследуемой нагрузки; 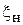 – положение минимума напряженности электрического поля (или напряжения) при установке на конце линии (волновода) короткозамыкающей перемычки; координата
– положение минимума напряженности электрического поля (или напряжения) при установке на конце линии (волновода) короткозамыкающей перемычки; координата 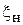 может быть названа условным концом линии, так как она находится на расстоянии целого числа полуволн от конца линии (волновода). При определении фазы φ коэффициента отражения от нагрузки по результатам измерений (1.28), (1.24) рекомендуется изобразить эскиз (рис. 1.6) взаимного расположения условных концов
может быть названа условным концом линии, так как она находится на расстоянии целого числа полуволн от конца линии (волновода). При определении фазы φ коэффициента отражения от нагрузки по результатам измерений (1.28), (1.24) рекомендуется изобразить эскиз (рис. 1.6) взаимного расположения условных концов 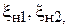 координаты минимума напряжения
координаты минимума напряжения 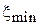 , нагрузки Н и генератора Г.
, нагрузки Н и генератора Г.
4. Модуль коэффициента отражения от заглушки 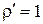 (1.22), так как падающая на заглушку волна полностью от нее отражается. В заглушке нет потерь СВЧ – энергии. Фаза коэффициента отражения от заглушки может быть определена следующим образом.
(1.22), так как падающая на заглушку волна полностью от нее отражается. В заглушке нет потерь СВЧ – энергии. Фаза коэффициента отражения от заглушки может быть определена следующим образом.
Вектор напряженности электрического поля в волноведущей структуре ориентирован перпендикулярно направлению распространения волн, т. е. касательно к поверхности заглушки. Это свойство характерно для волн длинной линии и волны основного типа (моды) в волноводе. Следовательно, полное электрическое поле на заглушке, представляемое суммой полей падающей и отраженной волн, будучи касательным к заглушке, равно нулю:
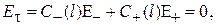 (1.25)
(1.25)
так как удельная электрическая проводимость металла заглушки принимается равной бесконечности: 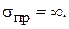 Аналогичное уравнение записывается для напряжения на заглушке:
Аналогичное уравнение записывается для напряжения на заглушке:
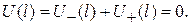 (1.26)
(1.26)
Из уравнений (1.25). (1.26) видно, что отраженная волна на заглушке полностью компенсирует падающую волну, и коэффициент отражения от заглушки оказывается равным (1.22):
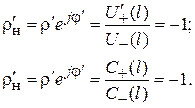
5. Подстановка значений 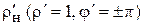 из (1.22) в формулы (1.11), (1.12). (1.15) дает для короткозамкнутой волноведущей структуры следующие значения:
из (1.22) в формулы (1.11), (1.12). (1.15) дает для короткозамкнутой волноведущей структуры следующие значения:
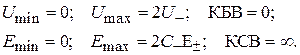 (1.27)
(1.27)
Подстановка (1.22) в формулы (1.5), (1.6), (1.8), (1.9) позволяет получить распределение модуля напряжения, или напряженности электрического поля вдоль волноведущей структуры:
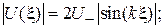 (1.28)
(1.28)
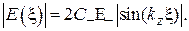 (1.29)
(1.29)
6. Итак, в случае короткозамкнутой волноведущей структуры амплитуды падающей и отраженной волн равны друг другу, в минимумах происходит полная взаимная компенсация падающей и отраженной волн, все минимумы равны нулю (рис. 1.5, б), а максимумы – удвоенному значению амплитуды падающей волны. Такой режим в волноведущей структуре, характеризующийся формулами (1.27)–(1.29), называется режимом стоячей волны. Максимумы стоячей волны называются пучностями, а минимумы – узлами. Расстояние между соседними минимумами – узлами равно половине длины волны (0,5l и 0,5lz). В короткозамкнутой волноведущей структуре все узлы электрического поля (или напряжения) находятся на расстоянии целого числа полуволн от ее конца. Сечения, отстоящие от конца волноведущей структуры на расстоянии целого числа полуволн, называются «условными концами» волноведущей структуры (длинной линии или волновода).
