Применение метода наименьших квадратов в Excel

Метод наименьших квадратов представляет собой математическую процедуру построения линейного уравнения, которое бы наиболее точно соответствовало набору двух рядов чисел. Целью применения данного способа является минимизация общей квадратичной ошибки. В программе Excel имеются инструменты, с помощью которых можно применять данный метод при вычислениях. Давайте разберемся, как это делается.

Содержание

· Использование метода в Экселе

o Включение надстройки «Поиск решения»

o Условия задачи

o Решение

Использование метода в Экселе

Метод наименьших квадратов (МНК) является математическим описанием зависимости одной переменной от второй. Его можно использовать при прогнозировании.

Включение надстройки «Поиск решения»

Для того, чтобы использовать МНК в Экселе, нужно включить надстройку «Поиск решения», которая по умолчанию отключена.

1. Переходим во вкладку «Файл».

2. Кликаем по наименованию раздела «Параметры».

3. В открывшемся окне останавливаем выбор на подразделе «Надстройки».

4. В блоке «Управление», который расположен в нижней части окна, устанавливаем переключатель в позицию «Надстройки Excel» (если в нём выставлено другое значение) и жмем на кнопку «Перейти…».

5. Открывается небольшое окошко. Ставим в нём галочку около параметра «Поиск решения». Жмем на кнопку «OK».

Теперь функция Поиск решения в Excel активирована, а её инструменты появились на ленте.

Урок: Поиск решения в Экселе

Условия задачи

Опишем применение МНК на конкретном примере. Имеем два ряда чисел x и y, последовательность которых представлена на изображении ниже.

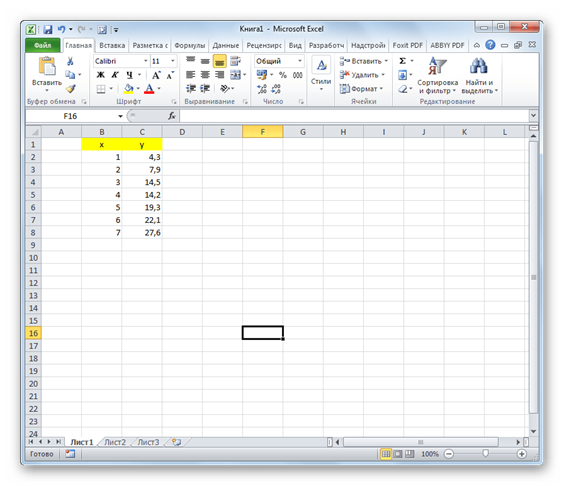
Наиболее точно данную зависимость может описать функция:

y=a+nx

При этом, известно что при x=0 y тоже равно 0. Поэтому данное уравнение можно описать зависимостью y=nx.

Нам предстоит найти минимальную сумму квадратов разности.

Решение

Перейдем к описанию непосредственного применения метода.

1. Слева от первого значения x ставим цифру 1. Это будет приближенная величина первого значения коэффициента n.

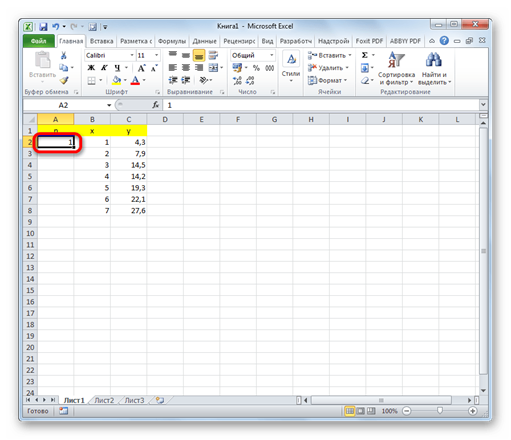
2. Справа от столбца y добавляем ещё одну колонку – nx. В первую ячейку данного столбца записываем формулу умножения коэффициента n на ячейку первой переменной x. При этом, ссылку на поле с коэффициентом делаем абсолютной, так как это значение меняться не будет. Кликаем по кнопке Enter.

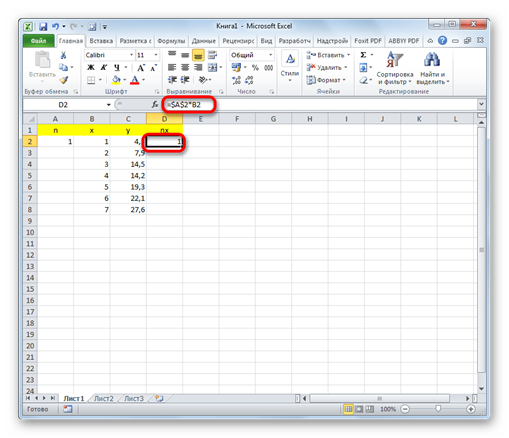
3. Используя маркер заполнения, копируем данную формулу на весь диапазон таблицы в столбце ниже.

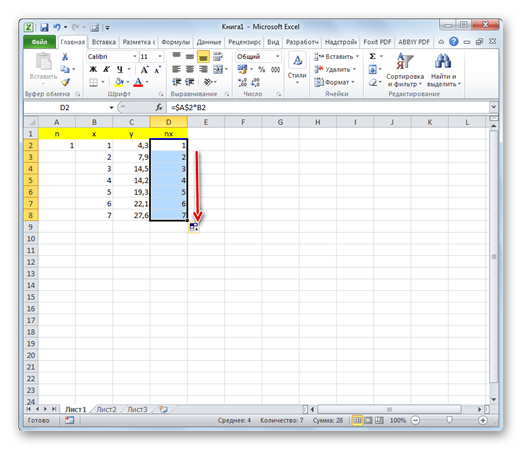
4. В отдельной ячейке высчитываем сумму разностей квадратов значений y и nx. Для этого кликаем по кнопке «Вставить функцию».

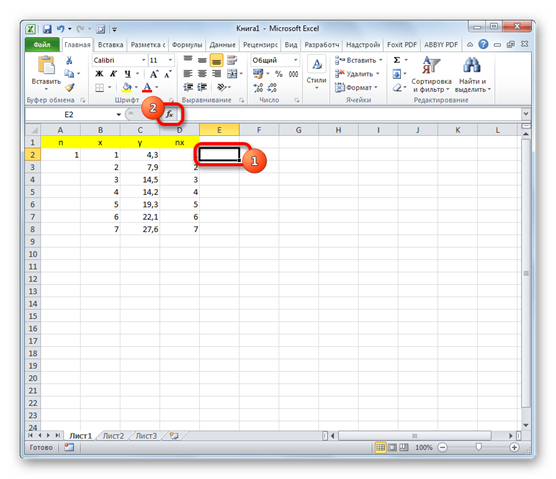
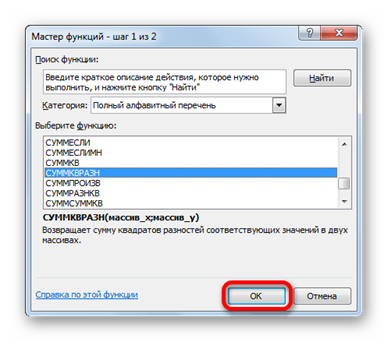
5. В открывшемся «Мастере функций» ищем запись «СУММКВРАЗН». Выбираем её и жмем на кнопку «OK».

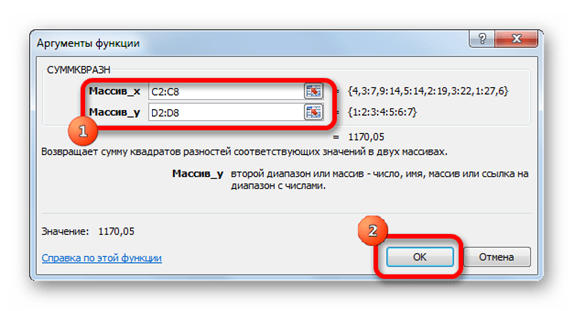
6. Открывается окно аргументов. В поле «Массив_x» вводим диапазон ячеек столбца y. В поле «Массив_y»вводим диапазон ячеек столбца nx. Для того, чтобы ввести значения, просто устанавливаем курсор в поле и выделяем соответствующий диапазон на листе. После ввода жмем на кнопку «OK».

7. Переходим во вкладку «Данные». На ленте в блоке инструментов «Анализ» жмем на кнопку «Поиск решения».

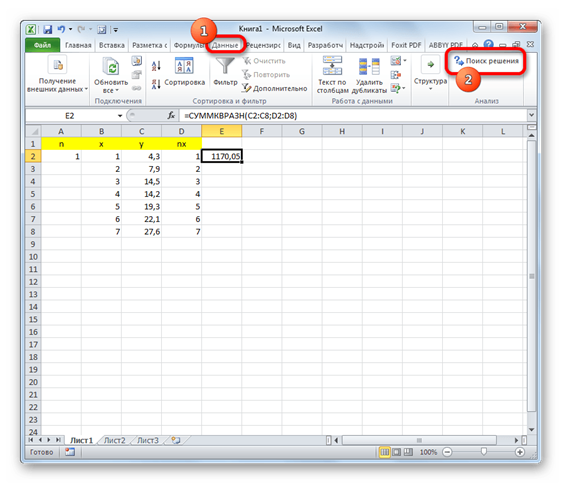
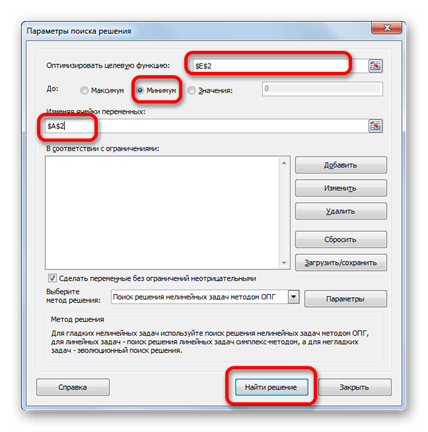
8. Открывается окно параметров данного инструмента. В поле «Оптимизировать целевую функцию»указываем адрес ячейки с формулой «СУММКВРАЗН». В параметре «До» обязательно выставляем переключатель в позицию «Минимум». В поле «Изменяя ячейки» указываем адрес со значением коэффициента n. Жмем на кнопку «Найти решение».

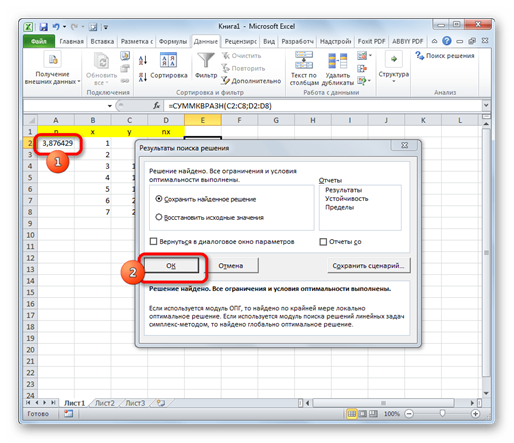
9. Решение будет отображаться в ячейке коэффициентаn. Именно это значение будет являться наименьшим квадратом функции. Если результат удовлетворяет пользователя, то следует нажать на кнопку «OK» в дополнительном окне.

Как видим, применение метода наименьших квадратов довольно сложная математическая процедура. Мы показали её в действии на простейшем примере, а существуют гораздо более сложные случаи. Впрочем, инструментарий Microsoft Excel призван максимально упростить производимые вычисления.

http://multitest.semico.ru/mnk.htm

Общие положения

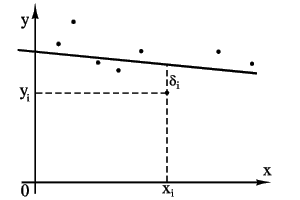Для упрощения изложения рассмотрим сначала случай линейной функции одного аргумента. Пусть из опыта получены точки:

x1, y1,
x2, y2, ...		(1)
xn, yn

(см. рисунок). Требуется найти уравнение прямой

y=ax+b,

(2)

наилучшим образом согласующейся с опытными точками.

Пусть мы нашли такую прямую. Обозначим через 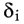расстояние опытной точки от этой прямой (измеренное параллельно оси y).

Из уравнения (2) следует, что

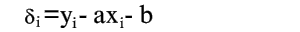(3)

Чем меньше числа 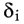по абсолютной величине, тем лучше подобрана прямая (2). В качестве характеристики точности подбора прямой (2) можно принять сумму квадратов

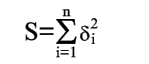(4)

Покажем, как можно подобрать прямую (2) так, чтобы сумма квадратов S была минимальной. Из уравнений (3) и (4) получаем

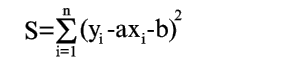(5)

Условия минимума S будут

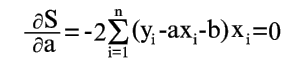	(6)
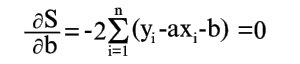	(7)

Уравнения (6) и (7) можно записать в таком виде:

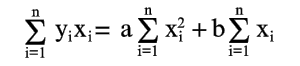	(8)
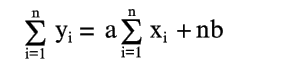	(9)

Из уравнений (8) и (9) легко найти a и b по опытным значениям x_i и y_i. Прямая (2), определяемая уравнениями (8) и (9), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (8) и (9), из которых определяется прямая (2), называются нормальными уравнениями.

Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки (1) и уравнение (2), можно записать систему уравнений для a и b

y1=ax1+b,
y2=ax2+b, ...		(10)
yn=axn+b,

Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т.е. на x₁, x₂, ..., x_n) и сложим полученные уравнения, в результате получится первое нормальное уравнение (8).

Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т.е. на 1, и сложим полученные уравнения, в результате получится второе нормальное уравнение (9).

Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции

y=a0+a1x+a2x2+...+anxn.

(11)

Естественно, что здесь получится система из n+1 нормального уравнения для определения величин
a₀, a₁, a₂, ..., a_n.

Рассмотрим частный случай применения метода наименьших квадратов. Пусть из теории известно, что

k=y/x

(12)

есть величина постоянная и ее нужно определить по опытным данным (1).

Систему уравнений для k можно записать:

k=y1/x1,
k=y2/x2, ...		(13)
k=yn/xn,

Для получения нормального уравнения умножим каждое из этих уравнений на коэффициент при неизвестной k, т.е. на 1, и сложим полученные уравнения

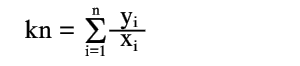(14)

отсюда

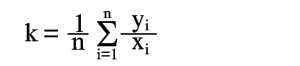(15)

Следовательно, среднее арифметическое, полученное из опытных отношений y_i/x_i, дает решение поставленной задачи по методу наименьших квадратов. Это важное свойство средней арифметической объясняет ее широкое применение в практике обработки опытных данных.

Пример 1

На опыте получены значения x и y, сведенные в таблицу

x
y	5,2	6,3	7,1	8,5	9,2	10,0

Найти прямую (2) по методу наименьших квадратов.

Решение. Находим:

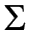x_i=21, 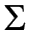y_i=46,3, 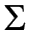x_i²=91, 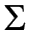x_iy_i=179,1.

Записываем уравнения (8) и (9)91a+21b=179,1,

21a+6b=46,3, отсюда находим
a=0,98 b=4,3.