Суть метода наименьших квадратов (МНК).

Метод наименьших квадратов

На заключительном уроке темы мы познакомимся с наиболее известным приложением ФНП, которое находит самое широкое применение в различных областях науки и практической деятельности. Это может быть физика, химия, биология, экономика, социология, психология и так далее, так далее. Волею судьбы мне часто приходится иметь дело с экономикой, и поэтому сегодня я оформлю вам путёвку в удивительную страну под названием Эконометрика =) …Как это не хотите?! Там очень хорошо – нужно только решиться! …Но вот то, что вы, наверное, определённо хотите – так это научиться решать задачи методом наименьших квадратов. И особо прилежные читатели научатся решать их не только безошибочно, но ещё и ОЧЕНЬ БЫСТРО ;-) Но сначала общая постановка задачи + сопутствующий пример:

Пусть в некоторой предметной области исследуются показатели 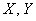, которые имеют количественное выражение. При этом есть все основания полагать, что показатель 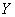зависит от показателя 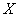. Это полагание может быть как научной гипотезой, так и основываться на элементарном здравом смысле. Оставим, однако, науку в сторонке и исследуем более аппетитные области – а именно, продовольственные магазины. Обозначим через:

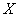– торговую площадь продовольственного магазина, кв.м.,
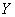– годовой товарооборот продовольственного магазина, млн. руб.

Совершенно понятно, что чем больше площадь магазина, тем в большинстве случаев будет больше его товарооборот.

Предположим, что после проведения 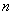наблюдений/опытов/подсчётов/танцев с бубном в нашем распоряжении оказываются числовые данные:

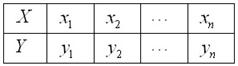
С гастрономами, думаю, всё понятно: 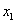– это площадь 1-го магазина, 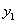– его годовой товарооборот, 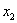– площадь 2-го магазина, 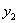– его годовой товарооборот и т.д. Кстати, совсем не обязательно иметь доступ к секретным материалам – довольно точную оценку товарооборота можно получить средствами математической статистики. Впрочем, не отвлекаемся, курс коммерческого шпионажа – он уже платный =)

Табличные данные также можно записать в виде точек 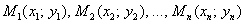и изобразить в привычной для нас декартовой системе .

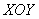Ответим на важный вопрос: сколько точек нужно для качественного исследования?

Чем больше, тем лучше. Минимально допустимый набор состоит из 5-6 точек. Кроме того, при небольшом количестве данных в выборку нельзя включать «аномальные» результаты. Так, например, небольшой элитный магазин может выручать на порядки больше «своих коллег», искажая тем самым общую закономерность, которую и требуется найти!

Если совсем просто – нам нужно подобрать функцию 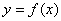, график которой проходит как можно ближе к точкам 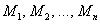. Такую функцию называют аппроксимирующей(аппроксимация – приближение) или теоретической функцией. Вообще говоря, тут сразу появляется очевидный «претендент» – многочлен высокой степени, график которого проходит через ВСЕ точки. Но этот вариант сложен, а зачастую и просто некорректен (т.к. график будет всё время «петлять» и плохо отражать главную тенденцию).

Таким образом, разыскиваемая функция должна быть достаточно простА и в то же время отражать зависимость адекватно. Как вы догадываетесь, один из методов нахождения таких функций и называется методом наименьших квадратов. Сначала разберём его суть в общем виде. Пусть некоторая функция 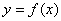приближает экспериментальные данные :

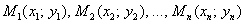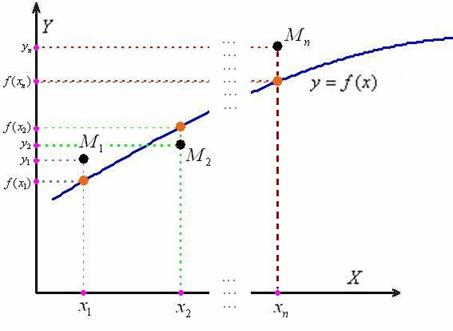
Как оценить точность данного приближения? Вычислим 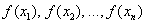и разности (отклонения) 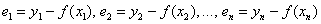между экспериментальными и функциональными значениями (изучаем чертёж). Первая мысль, которая приходит в голову – это оценить, насколько великА сумма 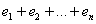, но проблема состоит в том, что разности могут быть и отрицательны (например, 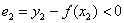) и отклонения в результате такого суммирования будут взаимоуничтожаться. Поэтому в качестве оценки точности приближения напрашивается принять сумму модулей отклонений:

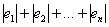или в свёрнутом виде: 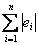(вдруг кто не знает: 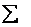– это значок суммы, а 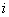– вспомогательная переменная-«счётчик», которая принимает значения от 1 до ).

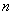Приближая экспериментальные точки различными функциями, мы будет получать разные значения 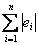, и очевидно, где эта сумма меньше – та функция и точнее.

Такой метод существует и называется он методом наименьших модулей. Однако на практике получил гораздо бОльшее распространение метод наименьших квадратов, в котором возможные отрицательные значения ликвидируются не модулем, а возведением отклонений в квадрат:

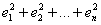, после чего усилия направлены на подбор такой функции 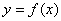, чтобы сумма квадратов отклонений 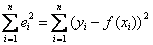была как можно меньше. Собственно, отсюда и название метода.

И сейчас мы возвращаемся к другому важному моменту: как отмечалось выше, подбираемая функция должна быть достаточно простА – но ведь и таких функций тоже немало: линейная, гиперболическая, экспоненциальная, логарифмическая, квадратичная и т.д. И, конечно же, тут сразу бы хотелось «сократить поле деятельности». Какой класс функций выбрать для исследования? Примитивный, но эффективный приём:

– Проще всего изобразить точки 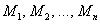на чертеже и проанализировать их расположение. Если они имеют тенденцию располагаться по прямой, то следует искать уравнение прямой 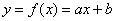с оптимальными значениями 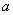и . И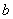ными словами, задача состоит в нахождении ТАКИХ коэффициентов 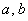– чтобы сумма квадратов отклонений 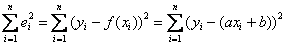была наименьшей.

Если же точки расположены, например, по гиперболе, то заведомо понятно, что линейная функция будет давать плохое приближение. В этом случае ищем наиболее «выгодные» коэффициенты 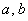для уравнения гиперболы 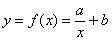– те, которые дают минимальную сумму квадратов .

А теперь обратите внимание, что в обоих случаях речь идёт о функции двух переменных, аргументами которой являются параметры разыскиваемых зависимостей:

И по существу нам требуется решить стандартную задачу – найти минимум функции двух переменных.

Вспомним про наш пример: предположим, что «магазинные» точки 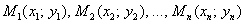имеют тенденцию располагаться по прямой линии и есть все основания полагать наличие линейной зависимости 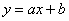товарооборота от торговой площади. Найдём ТАКИЕ коэффициенты «а» и «бэ», чтобы сумма квадратов отклонений 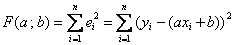была наименьшей. Всё как обычно – сначала частные производные 1-го порядка. Согласно правилу линейности дифференцировать можно прямо под значком суммы:

Если хотите использовать данную информацию для реферата или курсовика – буду очень благодарен за поставленную ссылку в списке источников, такие подробные выкладки найдёте мало где:

Составим стандартную систему:

Сокращаем каждое уравнение на «двойку» и, кроме того, «разваливаем» суммы:

Примечание: самостоятельно проанализируйте, почему «а» и «бэ» можно вынести за значок суммы. Кстати, формально это можно проделать и с суммой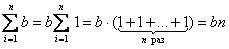

Перепишем систему в «прикладном» виде:

после чего начинает прорисовываться алгоритм решения нашей задачи:

Координаты точек 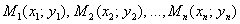мы знаем? Знаем. Суммы 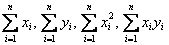найти можем? Легко. Составляем простейшуюсистему двух линейных уравнений с двумя неизвестными(«а» и «бэ»). Систему решаем, например, методом Крамера, в результате чего получаем стационарную точку 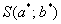. Проверяя достаточное условие экстремума, можно убедиться, что в данной точке функция 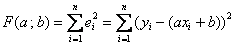достигает именно минимума. Проверка сопряжена с дополнительными выкладками и поэтому оставим её за кадром (при необходимости недостающий кадр можно посмотреть здесь). Делаем окончательный вывод:

Функция 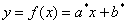наилучшим образом (по крайне мере, по сравнению с любой другой линейной функцией) приближает экспериментальные точки 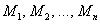. Грубо говоря, её график проходит максимально близко к этим точкам. В традициях эконометрикиполученную аппроксимирующую функцию также называют уравнением пАрной линейной регрессии.

Рассматриваемая задача имеет большое практическое значение. В ситуации с нашим примером, уравнение 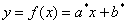позволяет прогнозировать, какой товарооборот («игрек») будет у магазина при том или ином значении торговой площади (том или ином значении «икс»). Да, полученный прогноз будет лишь прогнозом, но во многих случаях он окажется достаточно точным.

Я разберу всего лишь одну задачу с «реальными» числами, поскольку никаких трудностей в ней нет – все вычисления на уровне школьной программы 7-8 класса. В 95 процентов случаев вам будет предложено отыскать как раз линейную функцию, но в самом конце статьи я покажу, что ничуть не сложнее отыскать уравнения оптимальной гиперболы, экспоненты и некоторых других функций.

По сути, осталось раздать обещанные плюшки – чтобы вы научились решать такие примеры не только безошибочно, но ещё и быстро. Внимательно изучаем стандарт:

Задача

В результате исследования взаимосвязи двух показателей, получены следующие пары чисел:

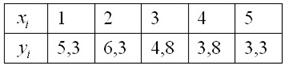
Методом наименьших квадратов найти линейную функцию, которая наилучшим образом приближает эмпирические (опытные) данные. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки 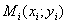и график аппроксимирующей функции 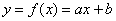. Найти сумму квадратов отклонений между эмпирическими 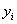и теоретическими 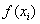значениями. Выяснить, будет ли функция 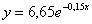лучше (с точки зрения метода наименьших квадратов) приближать экспериментальные точки.

Заметьте, что «иксовые» значения – натуральные, и это имеет характерный содержательный смысл, о котором я расскажу чуть позже; но они, разумеется, могут быть и дробными. Кроме того, в зависимости от содержания той или иной задачи как «иксовые», так и «игрековые» значения полностью или частично могут быть отрицательными. Ну а у нас дана «безликая» задача, и мы начинаем её решение:

Коэффициенты 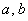оптимальной функции 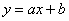найдём как решение системы:

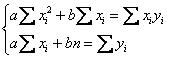
В целях более компактной записи переменную-«счётчик» можно опустить, поскольку и так понятно, что суммирование осуществляется от 1 до .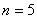

Расчёт нужных сумм удобнее оформить в табличном виде:

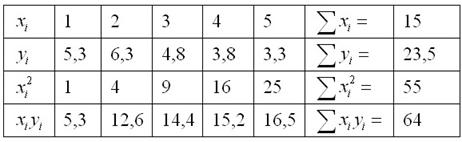
Вычисления можно провести на микрокалькуляторе, но гораздо лучше использовать Эксель – и быстрее, и без ошибок; смотрим короткий видеоролик:

Таким образом, получаем следующую систему:

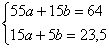
Тут можно умножить второе уравнение на 3 и из 1-го уравнения почленно вычесть 2-е. Но это везение – на практике системы чаще не подарочны, и в таких случаях спасает метод Крамера:
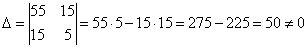, значит, система имеет единственное решение.

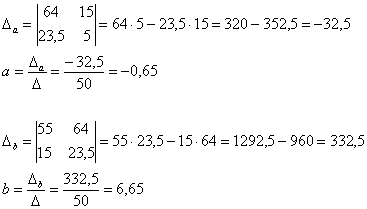
Выполним проверку. Понимаю, что не хочется, но зачем же пропускать ошибки там, где их можно стопроцентно не пропустить? Подставим найденное решение 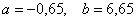в левую часть каждого уравнения системы:

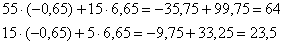
Получены правые части соответствующих уравнений, значит, система решена правильно.

Таким образом, искомая аппроксимирующая функция: 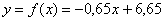– из всех линейных функций экспериментальные данные наилучшим образом приближает именно она.

В отличие от прямой зависимости товарооборота магазина от его площади, найденная зависимость является обратной (принцип «чем больше – тем меньше»), и этот факт сразу выявляется по отрицательному угловому коэффициенту. Функция 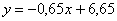сообщает нам о том, что с увеличение некоего показателя 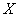на 1 единицу значение зависимого показателя 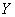уменьшается в среднем на 0,65 единиц. Как говорится, чем выше цена на гречку, тем меньше её продано.

Для построения графика аппроксимирующей функции найдём два её значения:

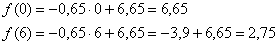
и выполним чертёж:

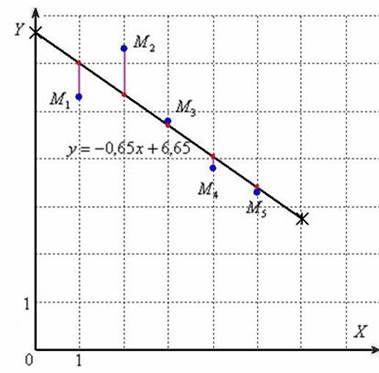
Построенная прямая называется линией тренда (а именно – линией линейного тренда, т.е. в общем случае тренд – это не обязательно прямая линия). Всем знакомо выражение «быть в тренде», и, думаю, что этот термин не нуждается в дополнительных комментариях.

Вычислим сумму квадратов отклонений 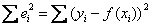между эмпирическими 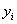и теоретическими 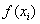значениями. Геометрически – это сумма квадратов длин «малиновых» отрезков (два из которых настолько малы, что их даже не видно).

Вычисления сведём в таблицу:

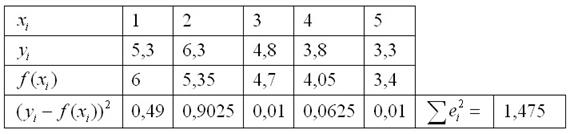
Их можно опять же провести вручную, на всякий случай приведу пример для 1-й точки:

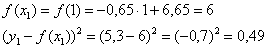
но намного эффективнее поступить уже известным образом:

Еще раз повторим: в чём смысл полученного результата? Из всех линейных функций у функции 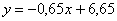показатель 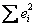является наименьшим, то есть в своём семействе это наилучшее приближение. И здесь, кстати, не случаен заключительный вопрос задачи: а вдруг предложенная экспоненциальная функция 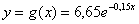будет лучше приближать экспериментальные точки?

Найдем соответствующую сумму квадратов отклонений 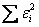– чтобы различать, я обозначу их буквой «эпсилон». Техника точно такая же:

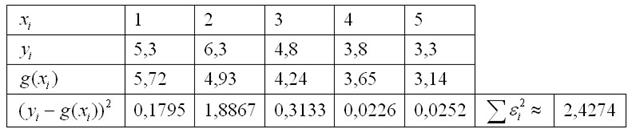
И снова на всякий пожарный вычисления для 1-й точки:

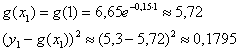
В Экселе пользуемся стандартной функцией EXP (синтаксис можно посмотреть в экселевской Справке).

Вывод: 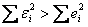, значит, экспоненциальная функция 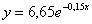приближает экспериментальные точки хуже, чем прямая .

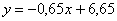Но тут следует отметить, что «хуже» – это ещё не значит, что плохо. Сейчас построил график этой экспоненциальной функции – и он тоже проходит близко к точкам 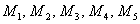– да так, что без аналитического исследования и сказать трудно, какая функция точнее.

На этом решение закончено, и я возвращаюсь к вопросу о натуральных значениях аргумента. В различных исследованиях, как правило, экономических или социологических, натуральными «иксами» нумеруют месяцы, годы или иные равные временнЫе промежутки. Рассмотрим, например, такую задачу:

Имеются следующие данные о розничном товарообороте магазина за первое полугодие:

Используя аналитическое выравнивание по прямой, определите объем товарооборота за июль.

Да без проблем: нумеруем месяцы 1, 2, 3, 4, 5, 6 и используем обычный алгоритм, в результате чего получаем уравнение 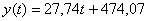– единственное, когда речь идёт о времени, то обычно используют букву «тэ» (хотя это не критично). Полученное уравнение показывает, что в первом полугодии товарооборот увеличивался в среднем на 27,74 д.е. за месяц. Получим прогноз на июль (месяц №7): 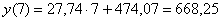д.е.

И подобных задач – тьма тьмущая. Желающие могут воспользоваться дополнительным сервисом, а именно моим экселевским калькулятором (демо-версия), который решает разобранную задачу практически мгновенно! Рабочая версия программы доступна по обмену или за символическую плaтy.

В заключение урока краткая информация о нахождение зависимостей некоторых других видов. Собственно, и рассказывать-то особо нечего, поскольку принципиальный подход и алгоритм решения остаются прежними.

Предположим, что расположение экспериментальных точек 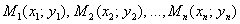напоминает гиперболу. Тогда чтобы отыскать коэффициенты 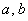наилучшей гиперболы 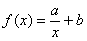, нужно найти минимум функции 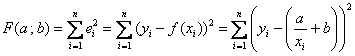– желающие могут провести подробные вычисления и прийти к похожей системе:

С формально-технической точки зрения она получается из «линейной» системы (обозначим её «звёздочкой») заменой «икса» на 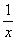. Ну а уж суммы-то 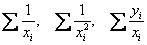рассчитаете, после чего до оптимальных коэффициентов «а» и «бэ» рукой подать.

Если есть все основания полагать, что точки 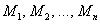располагаются по логарифмической кривой 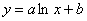, то для розыска оптимальных значени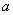й и 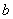находим минимум функции 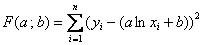. Формально в системе (*) нужно заменить 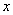на :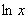

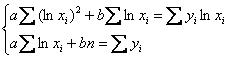
При вычислениях в Экселе используйте функцию LN. ПризнАюсь, мне не составит особого труда создать калькуляторы для каждого из рассматриваемых случаев, но всё-таки будет лучше, если вы сами «запрограммируете» вычисления. Видеоматериалы урока в помощь.

С экспоненциальной зависимостью 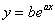ситуация чуть сложнее. Чтобы свести дело к линейному случаю, прологарифмируем функцию и воспользуемся свойствам логарифма:

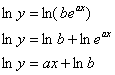
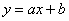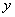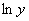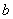Теперь, сопоставляя полученную функцию с линейной функцией , приходим к выводу, что в системе (*) нужно заменить на , а – на 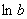. Для удобства обозначим :

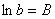Обратите внимание, что система разрешается относительно 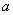и , и 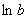поэтому после нахождения корней нужно не забыть найти сам коэффициент .

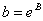Чтобы приблизить экспериментальные точки 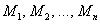оптимальной параболой 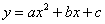, следует найти минимум функции трёх переменных 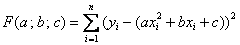. После осуществления стандартных действий получаем следующую «рабочую» систему:

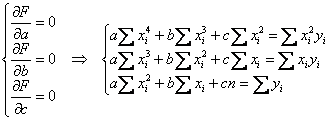
Да, конечно, сумм здесь побольше, но при использовании любимого приложения трудностей вообще никаких. И напоследок расскажу, как с помощью Экселя быстро выполнить проверку и построить нужную линию тренда: создаём точечную диаграмму, выделяем мышью любую из точек и через правый щелчок выбираем опцию «Добавить линию тренда». Далее выбираем тип диаграммы и на вкладке «Параметры»активируем опцию «Показывать уравнение на диаграмме». ОК

Как всегда статью хочется завершить какой-нибудь красивой фразой, и я уже чуть было не напечатал «Будьте в тренде!». Но вовремя передумал. И не из-за того, что она шаблонна. Не знаю, кому как, а мне что-то совсем не хочется следовать пропагандируемому американскому и в особенности европейскому тренду =) Поэтому я пожелаю каждому из вас придерживаться своей собственной линии!

http://www.grandars.ru/student/vysshaya-matematika/metod-naimenshih-kvadratov.html

Метод наименьших квадратов является одним из наиболее распространенных и наиболее разработанных вследствие своей простоты и эффективности методов оценки параметров линейныхэконометрических моделей. Вместе с тем, при его применении следует соблюдать определенную осторожность, поскольку построенные с его использованием модели могут не удовлетворять целому ряду требований к качеству их параметров и, вследствие этого, недостаточно “хорошо” отображать закономерности развития процесса .

Рассмотрим процедуру оценки параметров линейной эконометрической модели с помощью метода наименьших квадратов более подробно. Такая модель в общем виде может быть представлена уравнением (1.2):

y_t = a₀ + a₁ х_1t +...+ a_n х_nt + ε_t .

Исходными данными при оценке параметров a₀ , a₁ ,..., a_n является вектор значений зависимой переменной y = (y₁ , y₂ , ... , y_T )' и матрица значений независимых переменных

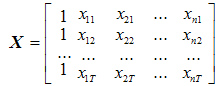
в которой первый столбец, состоящий из единиц, соответствует коэффициенту модели .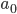

Название свое метод наименьших квадратов получил, исходя из основного принципа, которому должны удовлетворять полученные на его основе оценки параметров: сумма квадратов ошибки модели должна быть минимальной.

Примеры решения задач методом наименьших квадратов

Пример 2.1.Торговое предприятие имеет сеть, состоящую из 12 магазинов, информация о деятельности которых представлена в табл. 2.1.

Руководство предприятия хотело бы знать, как зависит размер годового товарооборота от торговой площади магазина.

Таблица 2.1

Номер магазина	Годовой товарооборот, млн руб.	Торговая площадь, тыс. м2
	19,76	0,24
	38,09	0,31
	40,95	0,55
	41,08	0,48
	56,29	0,78
	68,51	0,98
	75,01	0,94
	89,05	1,21
	91,13	1,29
	91,26	1,12
	99,84	1,29
	108,55	1,49

Решение методом наименьших квадратов.Обозначим 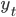— годовой товарооборот 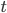-го магазина, млн руб.; 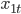— торговая площадь 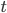-го магазина, тыс. м².

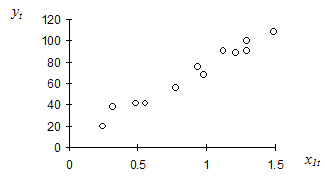
Рис.2.1. Диаграмма рассеяния для примера 2.1

Для определения формы функциональной зависимости между переменным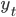и и 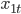построим диаграмму рассеяния (рис. 2.1).

На основании диаграммы рассеяния можно сделать вывод о позитивной зависимости годового товарооборота от торговой площади (т.е. у будет расти с ростом 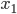). Наиболее подходящая форма функциональной связи — линейная.

Информация для проведения дальнейших расчетов представлена в табл. 2.2. С помощью метода наименьших квадратов оценим параметры линейной однофакторной эконометрической модели

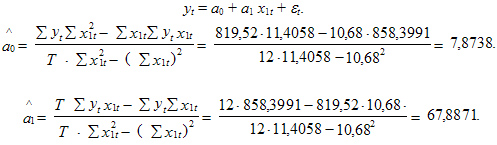
Таблица 2.2

t	yt	x1t	yt2	x1t 2	x1t yt
	19,76	0,24	390,4576	0,0576	4,7424
	38,09	0,31	1450,8481	0,0961	11,8079
	40,95	0,55	1676,9025	0,3025	22,5225
	41,08	0,48	1687,5664	0,2304	19,7184
	56,29	0,78	3168,5641	0,6084	43,9062
	68,51	0,98	4693,6201	0,9604	67,1398
	75,01	0,94	5626,5001	0,8836	70,5094
	89,05	1,21	7929,9025	1,4641	107,7505
	91,13	1,29	8304,6769	1,6641	117,5577
	91,26	1,12	8328,3876	1,2544	102,2112
	99,84	1,29	9968,0256	1,6641	128,7936
	108,55	1,49	11783,1025	2,2201	161,7395
S	819,52	10,68	65008,554	11,4058	858,3991
Среднее	68,29	0,89

Таким образом,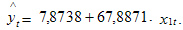

Cледовательно, при увеличении торговой площади на 1 тыс. м² при прочих равных условиях среднегодовой товарооборот увеличивается на 67,8871 млн руб.

Пример 2.2.Руководство предприятия заметило, что годовой товарооборот зависит не только от торговой площади магазина (см. пример 2.1), но и от среднего числа посетителей. Соответствующая информация представлена в табл. 2.3.

Таблица 2.3

Номер магазина	Среднее число посетителей в день, тыс. чел.
	8,25
	10,24
	9,31
	11,01
	8,54
	7,51
	12,36
	10,81
	9,89
	13,72
	12,27
	13,92

Решение.Обозначим 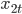— среднее число посетителей 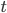-го магазина в день, тыс. чел.

Для определения формы функциональной зависимости между переменным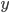и и 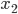построим диаграмму рассеяния (рис. 2.2).

На основании диаграммы рассеяния можно сделать вывод о позитивной зависимости годового товарооборота от среднего числа посетителей в день (т.е. у будет расти с ростом 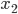). Форма функциональной зависимости — линейная.

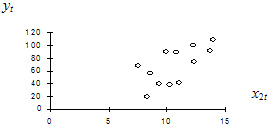
Рис. 2.2. Диаграмма рассеяния для примера 2.2

Таблица 2.4

t	x2t	x2t 2	yt x2t	x1t x2t
	8,25	68,0625	163,02	1,98
	10,24	104,8575	390,0416	3,1744
	9,31	86,6761	381,2445	5,1205
	11,01	121,2201	452,2908	5,2848
	8,54	72,9316	480,7166	6,6612
	7,51	56,4001	514,5101	7,3598
	12,36	152,7696	927,1236	11,6184
	10,81	116,8561	962,6305	13,0801
	9,89	97,8121	901,2757	12,7581
	13,72	188,2384	1252,0872	15,3664
	12,27	150,5529	1225,0368	15,8283
	13,92	193,7664	1511,016	20,7408
S	127,83	1410,44	9160,9934	118,9728
Cреднее	10,65

В целом необходимо определить параметры двухфакторной эконометрической модели

у_t = a₀ + a₁ х_1t + a₂ х_2t + ε_t

Информация, требующаяся для дальнейших расчетов, представлена в табл. 2.4.

Оценим параметры линейной двухфакторной эконометрической модели с помощью метода наименьших квадратов.

Таким образом,

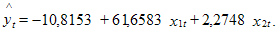
Оценка коэффициента 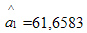=61,6583 показывает, что при прочих равных условиях с увеличением торговой площади на 1 тыс. м² годовой товарооборот увеличится в среднем на 61,6583 млн руб.

Оценка коэффициента 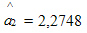= 2,2748 показывает, что при прочих равных условиях с увеличением среднего числа посетителей на 1 тыс. чел. в день годовой товарооборот увеличится в среднем на 2,2748 млн руб.

Пример 2.3.Используя информацию, представленную в табл. 2.2 и 2.4, оценить параметр однофакторной эконометрической модели

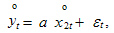
где 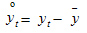— центрированное значение годового товарооборота 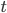-го магазина, млн руб.; 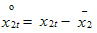— центрированное значение среднедневного числа посетителей t-го магазина, тыс. чел. (см. примеры 2.1-2.2).

Решение. Дополнительная информация, необходимая для расчетов, представлена в табл. 2.5.

Таблица 2.5

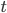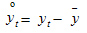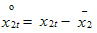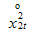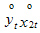	-48,53	-2,40	5,7720	116,6013
	-30,20	-0,41	0,1702	12,4589
	-27,34	-1,34	1,8023	36,7084
	-27,21	0,36	0,1278	-9,7288
	-12,00	-2,11	4,4627	25,3570
	0,22	-3,14	9,8753	-0,6809
	6,72	1,71	2,9156	11,4687
	20,76	0,16	0,0348	3,2992
	22,84	-0,76	0,5814	-17,413
	22,97	3,07	9,4096	70,4503
	31,55	1,62	2,6163	51,0267
	40,26	3,27	10,6766	131,5387
Cумма			48,4344	431,0566

Используя формулу (2.35), получим

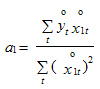
Таким образом,

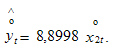
http://www.cleverstudents.ru/articles/mnk.html

Пример.

Экспериментальные данные о значениях переменных х и у приведены в таблице.

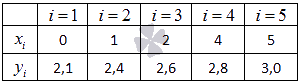
В результате их выравнивания получена функция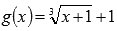

Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью y=ax+b (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж.

Решение.

В нашем примере n=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов.

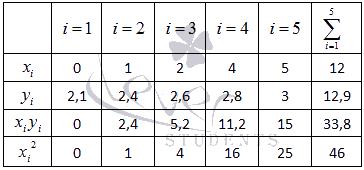
Значения в четвертой строке таблицы получены умножением значений 2-ой строки на значения 3-ей строки для каждого номера i .

Значения в пятой строке таблицы получены возведением в квадрат значений 2-ой строки для каждого номера i .

Значения последнего столбца таблицы – это суммы значений по строкам.

Используем формулы метода наименьших квадратов для нахождения коэффициентов а и b. Подставляем в них соответствующие значения из последнего столбца таблицы:

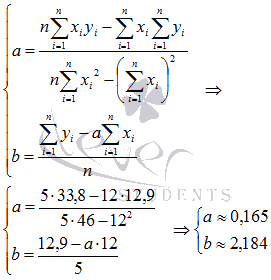
Следовательно, y = 0.165x+2.184 - искомая аппроксимирующая прямая.

Осталось выяснить какая из линий y = 0.165x+2.184 или 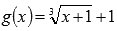лучше аппроксимирует исходные данные, то есть произвести оценку методом наименьших квадратов.

Доказательство.

Чтобы при найденных а и b функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции 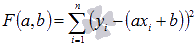была положительно определенной. Покажем это.

Дифференциал второго порядка имеет вид:

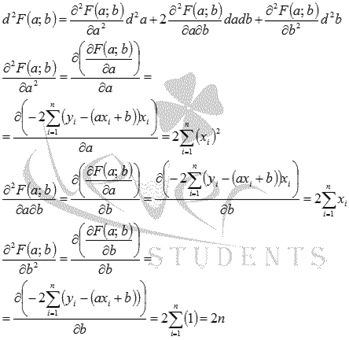
То есть

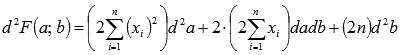
Следовательно, матрица квадратичной формы имеет вид

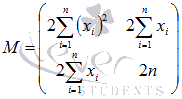
причем значения элементов не зависят от а и b .

Покажем, что матрица положительно определенная. Для этого нужно, чтобы угловые миноры были положительными.

Угловой минор первого порядка 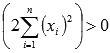. Неравенство строгое, так как точки <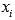