Решение линейных интегральных уравнений первого рода
I. ЦЕЛЬ РАБОТЫ
Приобретение навыков решения интегральных уравнений первого рода
II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Задачи для интегральных уравнений первого рода являются некорректно поставленными.
Рассмотрим уравнение Фредгольма первого рода
, 
, (1)
где ядро 
является непрерывной функцией по переменным 
; 
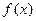- известная функция; 
- искомая функция.
Будем полагать, что уравнение (1) с точной правой частью 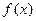имеет единственное решение.
Если вместо 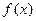известно лишь ее приближение 
, мало отличающееся (в метрике 
) от 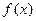, то можем искать лишь приближенное решение уравнения (1). В качестве приближенного решения уравнения (1) нельзя брать точное решение уравнения
. (2)
так как такого решения может не существовать. Кроме того, такое решение не обладает свойством устойчивости к малым изменениям правой части уравнения.
Будем искать решение уравнения (2) методом регуляризации. Согласно методу построим сглаживающий функционал 
, выбрав стабилизатор первого порядка 
:
, (3)
где 
- параметр регуляризации;
- заданные неотрицательные непрерывные функции (если нет специальных соображений по выбору функций , то обычно полагают 
). Затем найдем функцию 
, минимизирующую функционал (3), причем параметр 
определим по невязке, т.е. из условия
, (4)
где 
- уклонение правой части интегрального уравнения в метрике пространства , которое считаем известным:
Решение будет устойчиво к малым изменениям в метрике правой части уравнения .
Функция будет являться приближенным решением уравнения (1).
Для нахождения параметра регуляризации будем проводить расчеты с несколькими значениями параметра
(например, 
Для каждого значения находим функцию , минимизирующую функционал (3).
В качестве искомого значения параметра регуляризации возьмем такое число , для которого с требуемой точностью выполняется условие (4), т.е. невязка, полученная при подстановке найденной функции в уравнение (2), должна быть сравнима с погрешностью правой части интегрального уравнения.
Обратимся теперь к вариационной задаче
Полагая , получим
(5)
Проведем дискретизацию сглаживающего функционала, воспользовавшись разностным методом.
Аппроксимируем входящие в функционал интегралы квадратурными формулами. Для этого введем на прямоугольнике 
сетку 
, так, что 
.
Для простоты рассмотрим равномерную сетку 
где
.
Вычислим 
по формуле средних, заменяя производную разностным отношением
,
где 
.
Таким образом,
. (6)
Остальные интегралы вычислим по формуле трапеций
(7)
где
где 
(8)
где
Подставляя выражения (6) - (8) в (5), получим
(9)
Для решения задачи (9) приравняем к нулю производные от левой части (9) по 
. Получим систему уравнений, линейных относительно :
(10)
где
Систему (10) решим каким-либо методом, например, методом Гаусса.
Параметр следует подобрать способом, указанным выше. Заметим, что условие (4) в результате дискретизации запишем в виде:
III. ЗАДАНИЕ
Найти приближенное решение интегрального уравнения
полагая 
Здесь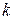 
- последняя цифра в номере группы; 
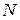- номер фамилии студента в журнале группы.
IV. ОФОРМЛЕНИЕ ОТЧЕТА
В отчете должны быть представлены:
1. Название работы.
2. Постановка задачи.
3. Описание алгоритма (метода) решения.
4. Текст программы с описанием.
5. Результаты работы программы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. — М.: Наука, 1979. 286 с.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.
3. Калиткин Н.Н. Численные методы. -М.: Наука, 1978. 512 с.