Решение систем линейных алгебраических уравнений методом гаусса с выбором главного элемента

Численные Методы

Направление подготовки: 01.03.02 «Прикладная математика и информатика»

Профиль подготовки: «Прикладная математика и информатика»

Направление подготовки: 02.03.01 «Математика и компьютерные науки»

Профиль подготовки: «Математическое и компьютерное моделирование»

Форма обучения: очная

Тула 2016 г.

Методические указания к лабораторным работам составлены профессором кафедры ПМиИ Толоконниковым Л.А. и обсуждены на заседании кафедры ПМиИ механико-математического факультета,

протокол № 10 от « 16 » мая 2016 г.

Зав. кафедрой ___________________ В.И. Иванов

Методические указания к лабораторным работам пересмотрены и утверждены на заседании кафедры ПМиИ механико-математического факультета,

протокол № ______ от « ____ » _______________ 20____ г.

Зав. кафедрой ___________________ В.И. Иванов

СОДЕРЖАНИЕ

Лабораторная работа № 1

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА

Лабораторная работа № 2

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ

Лабораторная работа № 3

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ЗЕЙДЕЛЯ

Лабораторная работа № 4

РЕШЕНИЕ СИСТЕМ С ТРЕХДИАГОНАЛЬНОЙ МАТРИЦЕЙ МЕТОДОМ ПРОГОНКИ

Лабораторная работа № 5

НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ МАТРИЦЫ МЕТОДОМ КРЫЛОВА

Лабораторная работа № 6

РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ МЕТОДОМ ДИХОТОМИИ

Лабораторная работа № 7

РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ МЕТОДОМ ИТЕРАЦИИ

Лабораторная работа № 8

РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ МЕТОДОМ НЬЮТОНА

Лабораторная работа № 9

ПРИМЕНЕНИЕ ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЫ ЛАГРАНЖА

Лабораторная работа № 10

ИНТЕРПОЛИРОВАНИЕ КУБИЧЕСКИМИ СПЛАЙНАМИ

Лабораторная работа № 11

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ ПО ФОРМУЛЕ ТРАПЕЦИЙ

Лабораторная работа № 12

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ ПО ФОРМУЛЕ СИМПСОНА

Лабораторная работа № 13

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ

МЕТОДОМ ЯЧЕЕК

Лабораторная работа № 14

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ

МЕТОДОМ ПОСЛЕДОВАТЕЛЬНОГО ИНТЕГРИРОВАНИЯ

Лабораторная работа № 15

РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ

УРАВНЕНИЙ МЕТОДОМ РУНГЕ – КУТТА

Лабораторная работа № 16

ПРИМЕНЕНИЕ РАЗНОСТНОГО МЕТОДА ДЛЯ РЕШЕНИЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ С

КРАЕВЫМИ УСЛОВИЯМИ

Лабораторная работа № 17

РЕШЕНИЕ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА МЕТОДОМ

СЕТОК

Лабораторная работа № 18

РЕШЕНИЕ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА МЕТОДОМ

СЕТОК

Лабораторная работа № 19

РЕШЕНИЕ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО ТИПА МЕТОДОМ

СЕТОК

Лабораторная работа № 20

РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ КВАДРАТУРНЫХ ФОРМУЛ

Лабораторная работа № 21

РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ МЕТОДОМ ЗАМЕНЫ

ЯДРА НА ВЫРОЖДЕННОЕ

Лабораторная работа № 22

РЕШЕНИЕ ПЛОХО ОБУСЛОВЛЕННЫХ СИСТЕМ ЛИНЕЙНЫХ

АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

Лабораторная работа № 23

РЕШЕНИЕ ЛИНЕЙНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО РОДА

Лабораторная работа № 1

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

2. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

Лабораторная работа №2

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков решения систем линейных алгебраических уравнений итерационными методами.

II. ТЕОРЕТИЧЕСКАЯ СПРАВКА

Рассмотрим метод простой итерации.

Пусть дана система линейных алгебраических уравнений

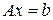
с неособенной матрицей ( 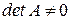). Согласно методу простой итерации ее предварительно приводят к виду

,

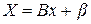где 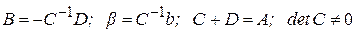, т.е. первое уравнение системы разрешили относительно 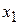, второе - относительно 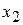и т.д.

Предположим, что известно начальное приближение

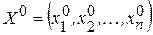
к точному решению 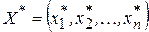системы. Тогда все следующие приближения найдем по формуле

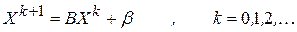
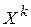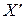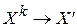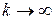Если последовательность сходится к некоторому предельному вектору , то он будет решением системы. Действительно, считая при , получаем из выражения

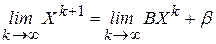
равенство .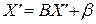

Последовательность 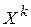в методе простой итерации сходится, если для матрицы 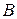выполняется одно из неравенств

1) ;

.

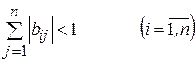III. ЗАДАНИЕ

Найти решение системы линейных уравнений, приведенной в лабораторной работе №1. При решении системы использовать метод простой итерации.

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.

Лабораторная работа № 3

МЕТОДОМ ЗЕЙДЕЛЯ

II. ЦЕЛЬ РАБОТЫ

Приобретение навыков решения систем линейных алгебраических уравнений итерационными методами.

III. ТЕОРЕТИЧЕСКАЯ СПРАВКА

Рассмотрим метод Зейделя.

Пусть система 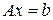приведена к канонической форме

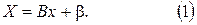
В методе простой итерации следующее приближение 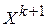находится по предыдущему 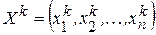путем подстановки 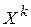в правую часть (1). При этом порядок выбора уравнений значения не имеет.

Согласно методу Зейделя осуществляется разумный выбор порядка уравнений для подстановок и немедленный ввод в вычисления каждого из полученных приближений для неизвестных.

Предположим, что для перехода от приближения 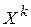к 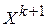выбран какой-то порядок привлечения уравнений для подстановок. Изменяя, если необходимо, нумерацию уравнений и неизвестных, можно считать, что уравнения для подстановок берутся в порядке роста их номеров. Для каждого шага порядок привлечения уравнений может быть своим. Перестановка уравнений и изменение нумераций влекут изменение матрицы 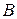и вектора 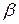. Чтобы отметить это, обозначим 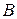и 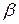для рассматриваемого шага через 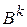и .

И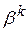терация в методе Зейделя выполняется в следующем порядке:

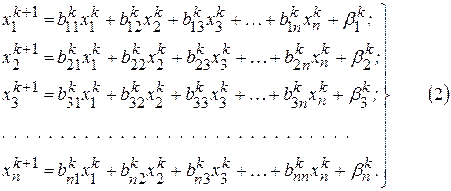
После нахождения вектора 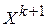устанавливается порядок подстановок в уравнения значений 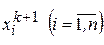и переходят к вычислению вектора 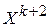и т.д.

Приведем теперь принцип установления порядка привлечения уравнений для подстановок 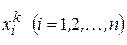. Можно пытаться улучшить ту составляющую решения, которая найдена наименее точно, чтобы при нахождении всех других составляющих употребить улучшенное ее значение.

О точности 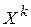можно судить по вектору поправки на шаг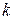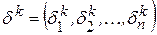е : , где 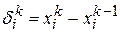. Величины поправок составляющих нумеруют в порядке убывания их модулей, и в том же порядке вычисляют составляющие следующего приближения 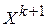, сначала ту составляющую, которая отвечает наибольшей по модулю поправке, и т.д.

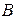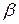Рассмотрим более подробно стационарный метод Зейделя, когда при итерациях порядок уравнений сохраняется, а следовательно, сохраняются и . Вычисления по-прежнему проводят по формуле (2).

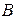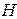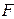Разложим матрицу на сумму двух матриц и , где

,

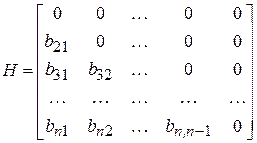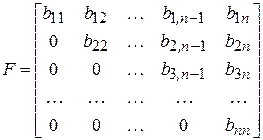
Тогда равенства (2) можно записать в матричной форме в виде

.

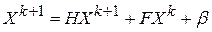Отсюда следует, что

,

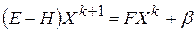а так как определитель матрицы 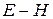равен единице и она имеет обратную матрицу, то равенство (2) равносильно

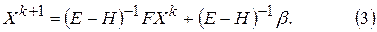
Поэтому стационарный метод Зейделя равносилен методу простой итерации, примененному к системе

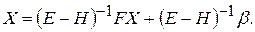
Последовательность 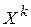в стационарном методе Зейделя сходится, если для матрицы 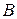выполняется одно из неравенств

2) ;

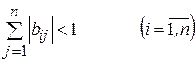3) .

IV. ЗАДАНИЕ

Найти решение системы линейных уравнений, приведенной в лабораторной работе №1. При решении системы использовать стационарный метод Зейделя.

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.

Лабораторная работа № 4

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

Лабораторная работа № 5

МАТРИЦЫ МЕТОДОМ КРЫЛОВА

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков отыскания собственных значений матрицы.

II. ТЕОРЕТИЧЕСКАЯ СПРАВКА

Рассмотрим один из методов развертывания характеристических определителей – метод Крылова.

Характеристический многочлен матрицы A имеет вид

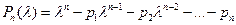. (1)

Согласно теореме Гамильтона-Кели матрица A обращает в ноль свой характеристический многочлен

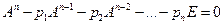. (2)

Возьмем произвольный ненулевой вектор 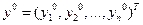. Умножая равенство (2) на этот вектор, получим

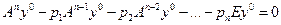. (3)

Положим

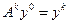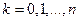( ). (4)

Тогда равенство (3) приобретает вид

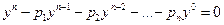, (5)

где ( ).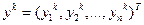

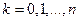Векторное равенство (5) эквивалентно системе уравнений

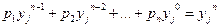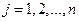( ). (6)

На основании формулы (4) имеем

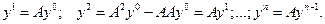
Поэтому

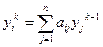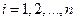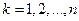( ; ). (7)

Таким образом, коэффициенты системы (6) вычисляются по формулам (7). Из системы линейных алгебраических уравнений (6) определяем неизвестные ( ).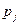

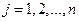Определив коэффициенты 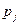( 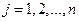), получим выражение для характеристического многочлена матрицы A. Теперь можем найти корни характеристического уравнения

,

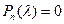которые являются собственными значениями матрицы A.

III. ЗАДАНИЕ

Построить характеристический многочлен матрицы A. Найти его корни.

Матрица A имеет элементы

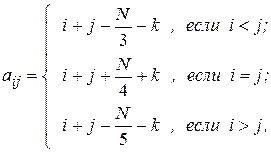
где 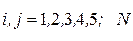- номер фамилии студента в журнале группы; 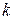- последняя цифра номера группы.

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Березин И.С., Жидков Н.П. Методы вычислений. Т.2. - М.: Физматгиз, 1966. 632 с.

2. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

Лабораторная работа № 6

ДИХОТОМИИ

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков нахождения с заданной погрешностью корней нелинейного уравнения.

II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Требуется найти корни уравнения

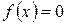, (1)

где 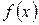- непрерывная функция.

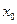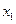Пусть нашли такие точки и , что 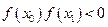, то есть на отрезке [ 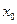, 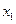] лежит по меньшей мере один корень. Найдем середину отрезка [ 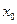, 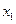] 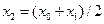и вычислим 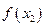. Если 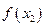=0, то 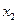есть корень 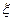. Если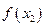 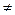0, то из двух половин отрезка [ 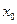, 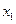] выберем ту, для которой 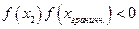, так как один корень лежит на этой половине. Затем новый отрезок делим пополам и выбираем ту половину, на концах которой функция 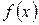имеет разные знаки. И так далее.

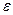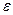Деление продолжаем до тех пор, пока длина очередного отрезка, где лежит корень, не станет меньше 2 , где - заданная погрешность. Тогда середина последнего отрезка даст значение корня с требуемой точностью.

III. ЗАДАНИЕ

Найти методом дихотомии один из действительных корней уравнения 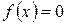с погрешностью .

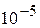Варианты задания:

№	Уравнение

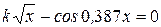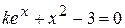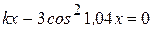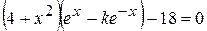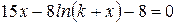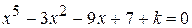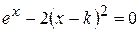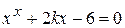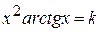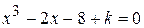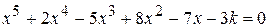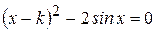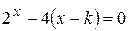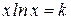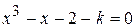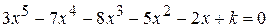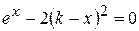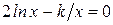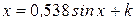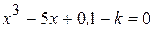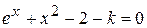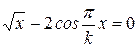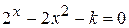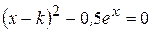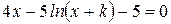Здесь 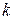- последняя цифра номера группы, 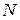- номер фамилии студента в журнале группы.

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

2. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

Лабораторная работа № 7

ИТЕРАЦИИ

II. ЦЕЛЬ РАБОТЫ

Приобретение навыков нахождения с заданной погрешностью корней нелинейного уравнения.

III. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Требуется найти корни уравнения

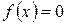, (1)

где 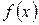- непрерывная функция.

Заменим исходное уравнение эквивалентным ему уравнением .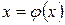

Выберем некоторое нулевое приближение 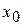и вычислим дальнейшие приближения по формуле

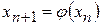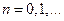( ). (2)

Если 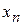стремится к некоторому пределу 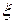, то этот предел есть корень исходного уравнения, т.е.

.

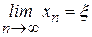Исследуем условия сходимости. Если 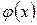имеет непрерывную производную, тогда (по теореме Лагранжа)

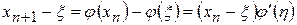, (3)

где точка 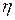лежит между точкам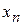и и 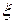. Поэтому, если всюду на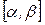 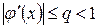, то отрезок 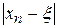убывает не медленней членов геометрической прогрессии со знаменателем 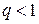и последовательность 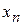сходится при любом начальном приближении .

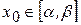Действительно, это видно из соотношений

.

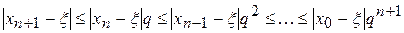Очевидно, чем меньше 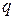, тем быстрее сходимость. Успех метода зависит от того, насколько удачно выбрано .

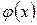Из выражения (3) видно, что, если 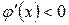, то итерации попеременно оказываются то с одной, то с другой стороны 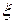, так что корень заключен в интервале 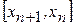. Это надежная, хотя несколько грубая оценка. Но она неприменима, когда 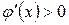, когда итерации сходятся к корню монотонно, т.е. с одной стороны.

Можно показать, что итерации следует прекращать, если выполняется условие

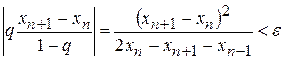, (4)

где 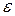- заданная точность.

Метод итераций имеет важное достоинство самоисправляемости. Ошибки вычислений в методе не накапливаются. Метод итераций устойчив даже к грубым ошибкам (сбоям ЭВМ), если только ошибка не выбрасывает очередное приближение за пределы области сходимости. Ошибочное приближение рассматривается как некоторое новое начальное.

IV. ЗАДАНИЕ

Найти методом итераций один из действительных корней уравнения 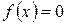с допустимой погрешностью .

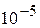Варианты задания приведены в лабораторной работе № 6.

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.

Лабораторная работа № 8

МЕТОДОМ НЬЮТОНА

II. ЦЕЛЬ РАБОТЫ

Приобретение навыков отыскания приближенных значений действительных корней уравнения методом Ньютона.

III. ТЕОРЕТИЧЕСКАЯ СПРАВКА

Требуется найти корни уравнения

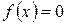, (1)

где 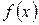- дифференцируемая функция.

Если 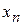есть некоторое приближение к корню 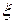, а 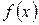имеет непрерывную производную, то уравнение (1) можно преобразовать следующим образом:

,

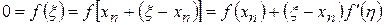где 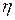- точка, лежащая между 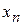и .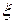

Приближенно заменяя 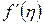на значение в известной точке 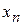, получим такой итерационный процесс:

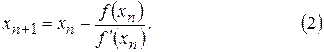
Геометрически этот процесс означает замену на каждой итерации графика 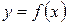касательной к нему.

Метод Ньютона можно рассматривать как частный случай метода итераций, если положить

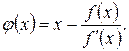
Тогда

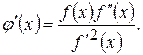
При произвольном начальном приближении итерации сходятся, если всюду на рассматриваемом интервале 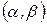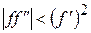(чтобы 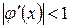, причем 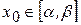). В противном случае сходимость будет не при любом начальном приближении, а только в некоторой окрестности корня.

Отметим еще достаточное условие сходимости итераций: есл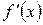и и 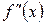отличны от нуля и сохраняют определенные знаки на 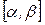, то исходя из начального приближения 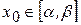, удовлетворяющего неравенству 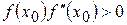, получим методом Ньютона значение корня с любой степенью точности. Т.о., в качестве исходной точки 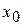следует выбирать тот конец 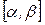, для которого 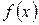и 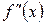имеют одинаковые знаки. Если взять такое 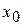, что 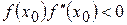, то мы можем не прийти к корню 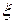, если только 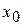не очень хорошее.

Оценим скорость сходимости метода Ньютона. Справедлива оценка

,

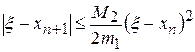где 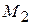- наибольшее значение 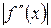на 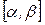, 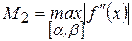; 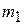- наименьшее значение 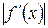на 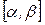, 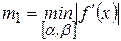. Отсюда видно, что погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Самый неблагоприятный случай для метода Ньютона, когда 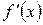становится малой вблизи корня. Чтобы не было потери точности, отношение 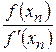надо вычислять достаточно аккуратно. К остальным погрешностям расчета метод Ньютона хорошо устойчив.

IV. ЗАДАНИЕ

Найти методом Ньютона один из действительных корней уравнения 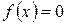с точностью 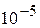. Варианты заданий приведены в лабораторной работе № 6.

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.

Лабораторная работа № 9

ЛАГРАНЖА

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков использования интерполяционных многочленов.

II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Пусть функция 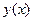задана таблично, т.е. известны ее значения в 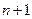точках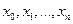

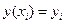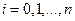( ). (1)

Построим многочлен 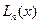степени 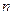такой, чтобы выполнялись интерполяционные условия

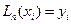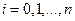( ). (2)

Сначала построим полином степени 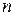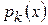, такой, что

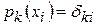, (3)

где 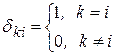- символ Кронекера.

Так как 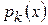обращается в нуль в 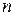точках 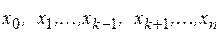, то он имеет вид

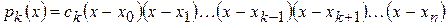, (4)

где 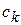- постоянный коэффициент.

Полагая в формуле (4) 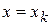и учитывая, что 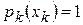, получим

.

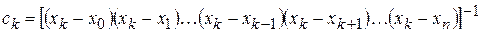Подставив этот коэффициент в (4), находим

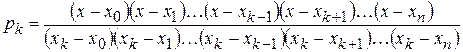. (5)

Теперь построим многочлен 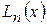, который имеет вид

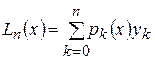. (6)

Степень 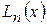, как видно из (5) и (6), не выше 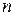. Кроме того, на основании (2)

,

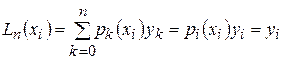что согласуется с (2)

Интерполяционный многочлен 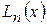называется многочленом Лагранжа и имеет вид

.

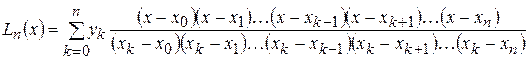Теперь считаем .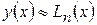

Для абсолютной погрешности интерполяционного многочлена Лагранжа справедлива оценка

,

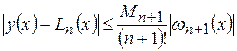где ;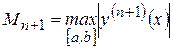

.

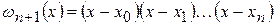III. ЗАДАНИЕ

Дана таблица значений функции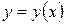

x	3,5	4,1	4,3
y	N+k	N+2k	N-k	N

Здесь 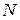- номер фамилии студента в журнале группы; 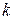- последняя цифра номера группы.

Построить интерполяционный многочлен Лагранжа. Вычислить с его помощью значения ; ; .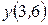

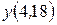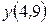IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

Лабораторная работа № 10

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функции. - М.: Наука, 1980. 248 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

Лабораторная работа № 11

ПО ФОРМУЛЕ ТРАПЕЦИЙ

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков приближенного вычисления интегралов с помощью квадратурных формул.

II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Пусть требуется вычислить интеграл .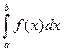

Разобьем отрезок 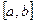с помощью равноотстоящих точек

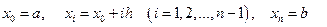
на 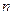равных частей. Шаг .

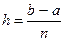Пусть = .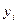

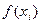Заменяя функцию 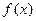многочленом Лагранжа

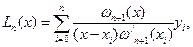
где ,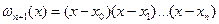

получаем квадратурную формулу

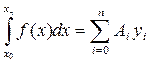. (1)

где

( ).

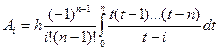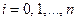При этом .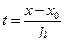

Полагая 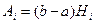, будем иметь

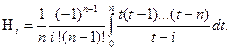(2)

Тогда квадратурная формула (1) принимает вид

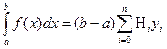. (3)

Формулы (2) и (3) называются формулами Ньютона – Котеса.

Полагая в формуле (2) 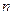=1, находим

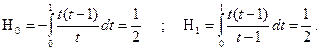
В результате получаем формулу трапеций

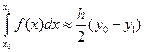. (4)

Для повышения точности на отрезке [a,b] вводится достаточно густая сетка

.

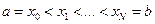Интеграл разбивается на сумму интегралов по шагам сетки и к каждому шагу применяют формулу (4).

Обобщенная формула трапеций на равномерной сетке с шагом 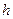имеет вид

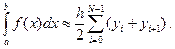(5)

Для равномерной сетки справедлива следующая мажорантная оценка погрешности формулы трапеций:

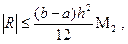
где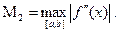

III. ЗАДАНИЕ

Вычислить с помощью формулы трапеций определенный интеграл от заданной функции.

Варианты заданий

Наши рекомендации

№

f(x)

Пределы интегрирования