Второй метод получения минимальных КНФ

Этот метод полностью опирается на преобразования дизъюнктивных форм переключательных функций. Алгоритм заключается в следующем.

1. Записывают дизъюнкцию всех конституент единицы, которые не входят в СДНФ заданной функции.

Если функция задана таблицей, то в эту форму войдут конституенты единицы, соответствующие наборам аргументов, на которых функция равна нулю. Если функция задана аналитически, то вначале находят ее совершенную ДНФ, а затем записывают дизъюнкцию всех конституент, которые не вошли в эту функцию. Можно показать, что полученная таким образом форма будет совершенной дизъюнктивной нормальной формой заданной функции, взятой с отрицанием.

2. Находят минимальные ДНФ по рассмотренным алгоритмам.

3. От полученных минимальных форм берут отрицания, и после пре­об­ра­зований по формулам де Моргана получают конъюнктивные формы, которые будут минимальными.

Для обоснования приведенного алгоритма получения минимальной КНФ доста­точно доказать два положения.

1. Дизъюнкция всех конституент единицы, не входящих в совершенную дизъюнктивную нормальную форму данной функции f(x₁, x₂, …, x_n), является отрицанием данной функции .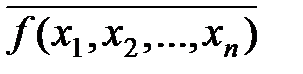

2. Преобразования по формулам де Моргана минимальной дизъ­юнк­тивной нормальной формы функции 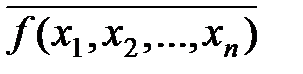приводят к получению минимальной конъюнктивной нормальной формы функции f(x₁, x₂, …, x_n).

Прежде всего заметим, что дизъюнкция всех конституент единицы тож­дественно равна единице. Действительно, для любого набора аргументов в такой дизъюнкции найдется конституента, равная на этом наборе единице. Но если одно логическое слагаемое ДНФ равно единице, то равна единице и вся дизъюнктивная форма. Поэтому справедливы такие, например, соот­но­шения:

,

.

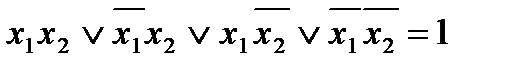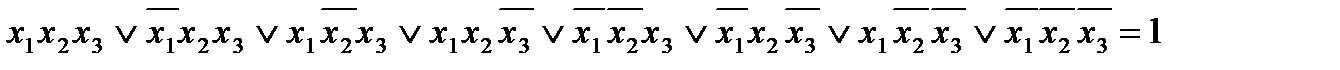В общем виде

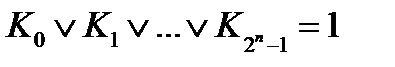, (2.5)

где n – число аргументов.

Рассмотрим некоторую ПФ, заданную в СДНФ:

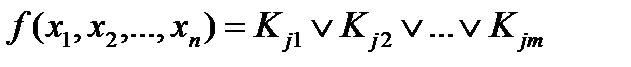, (2.6)

где m – число наборов, на которых ПФ равна единице.

Обозначим конституенты единицы, не входящие в последнее выра­же­ние, через 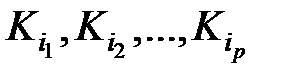, где p = 2ⁿ – m – число наборов, на которых функция равна нулю. Тогда на основании соотношения (2.5)

.

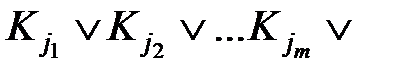
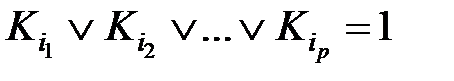Учитывая (2.6), получим

.

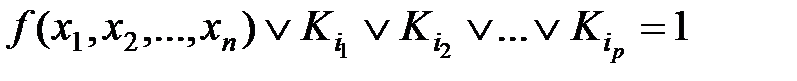Сравнивая последнее соотношение с тождеством х₁Ú 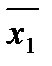= 1, которое можно записать в форме

,

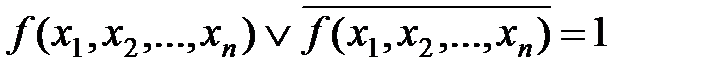получим

,

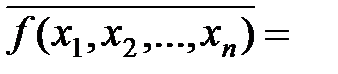
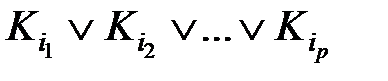что и требовалось доказать.

Преобразования по формулам де Моргана не изменяют число букв в выражении для ПФ. Поэтому если взять отрицание от минимальной ДНФ функции 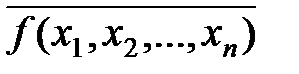, то полученная после преобразования по формулам де Моргана конъюнктивная форма также будет минимальной, но уже для функции .

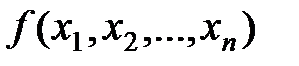Если предположить, что эта форма не является минимальной, то существует другая конъюнктивная форма, содержащая меньшее число букв. Тогда, взяв от нее отрицание и применив формулы де Моргана, получим дизъ­юнктивную форму с меньшим числом букв, чем в минимальной. Это противоречит определению минимальной формы и, следовательно, пред­по­ло­жение о том, что полученная конъюнктивная форма не является мини­мальной, не верно.

Пример 2.9. Найти минимальную конъюнктивную форму ПФ, заданной таблицей истинности (табл. 2.4).

Таблица 2.4.

Таблица истинности

Номер набора
x1
x2
x3
f(x1, x2, x3)

1. Запишем дизъюнкцию кон­ституент единицы, соответ­ствующих набо­рам, на ко­торых функция равна нулю:

.

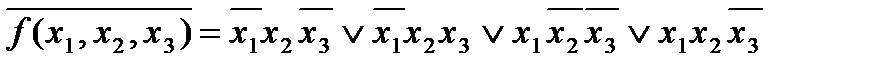2. Выполним операции неполного склеивания и поглощения, после чего получим сокра­щен­ную ДНФ функции :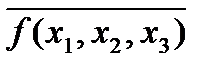

.

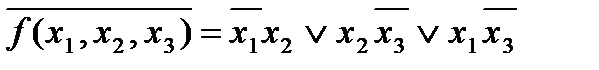3. Испытывая импликанты, обнаружим, что вторую импликанту можно исключить (при x₂ = 1, x₃ = 0, выражение 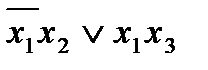º 1), т.е. минимальная ДНФ функции 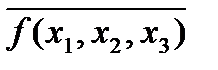имеет вид

.

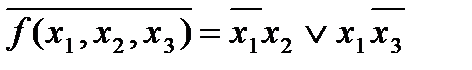Использовав формулу де Моргана, получим минимальную КНФ заданной функции:

.

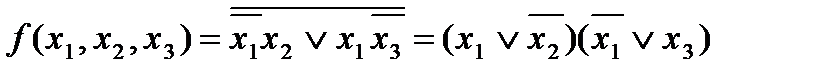Пример 2.10. Найти минимальную конъюнктивную нормальную форму функции

.

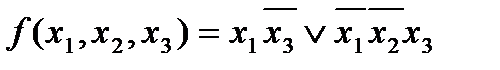1. Находим СДНФ:

.

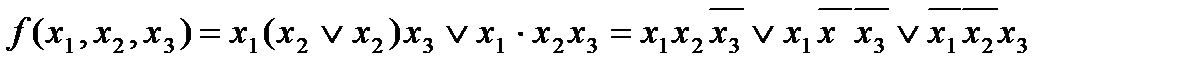2. Записав дизъюнкцию конституент единицы, не вошедших в преды­ду­щее выражение, получим СДНФ функции :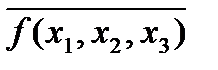

.

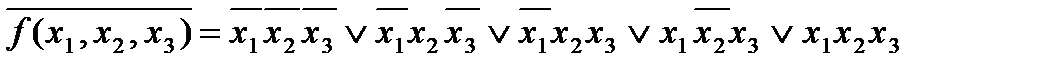3. Сокращенная ДНФ имеет вид

.

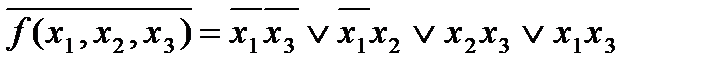4. Находим минимальные формы функции 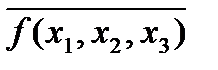, построив импликантную матрицу (табл.2.5).

Таблица 2.5

Импликантная матрица

Импли- канта	Конституента
x1x2 x3	x1x2 x3	x1x2 x3	x1x2 x3	x1x2 x3
x1 x3	*	*
x1 x2		*	*
x2 x3			*		*
x1 x3				*	*

1) .

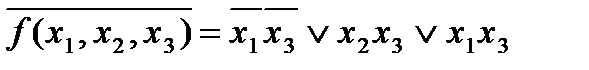2)

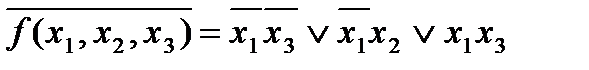
Воспользовавшись формулой де Моргана, получим две мини­маль­ные КНФ:

f(x₁, x₂, x₃) = (x₁Ú x₃)( x₂Ú x₃)( x₁Ú x₃).

f(x₁, x₂, x₃) = (x₁Ú x₃)( x₁Ú x₂)( x₁Ú x₃).