Минимизация переключательных функций с помощью диаграмм Вейча

Диаграммы Вейча позволяют упростить поиск склеивающихся конституент. Диаграмма Вейча – это специальная таблица, определяющая значения переключательной функции на каждом наборе аргументов. Каждой клетке диаграммы соответствует определенный набор значений аргументов (рис. 2.5.1,б).

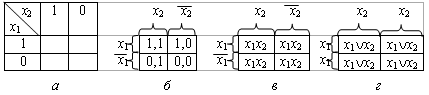
Рис. 2.1. Диаграмма Вейча для функции двух переменных

Склеивающиеся между собой конституенты единицы или нуля в диа­грам­мах Вейча для функций двух аргументов расположены в соседних смежных клет­ках (рис. 2.1, в, г).

Чтобы представить переключательную функцию диаграммой Вейча, сле­дует записать единицы в клетки, соответствующие наборам, на которых функция равна единице, и нули – в остальные клетки.

В диаграмме Вейча для переключательной функции двух аргументов лю­бая пара единиц, расположенных в соседних клетках, выражается одной буквой, которая при переходе от одной клетки к другой не изменяет знака инверсии.

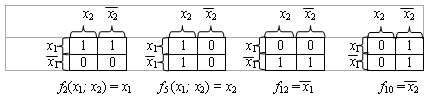
Рис. 2.2. Диаграммы Вейча для некторых функций двух переменных

Это обстоятельство используют для получения минимальных ДНФ и КНФ.

Рассмотрим диаграммы Вейча переключательной функции f₁₃(х₁; x₂) =

= х₁® x₂.

Рис. 2.3. Диаграмма Вейча для функции f₁₃(x₁;x₂)

Это выражение, являющееся минимальной формой функции f₁₃(x₁;x₂), получено путем склеивания конституент единиц, обведенных овалами.

Для 3-х переменных:

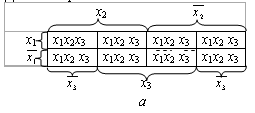
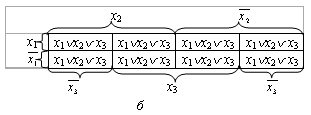
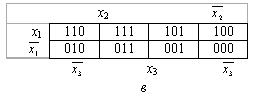
Рис. 2.4. Иллюстрации к построению диаграмм Вейча для функций трех пе­ре­менных: а – размещение конституент единицы; б – размещение кон­ституент нуля; в – соответствие клеток диаграммы и наборов значений аргументов

Эти диаграм­мы следует пред­став­­лять в виде ци­­линд­ра, образо­ванного соедине­ни­ем граней пер­вой и по­след­ней ко­ло­нок.

Тогда любая пара склеивающихся между собой конституент будет находится в соседних смежных клетках.

Рассмотрим диаграммы Вейча переключательных функций, которые могут быть представлены произведением двух переменных:

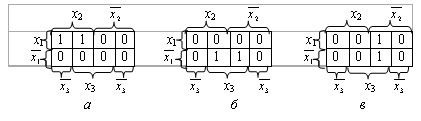
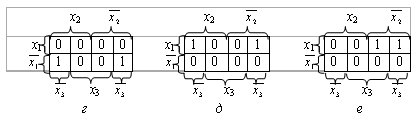
Рис. 2.5. Диаграммы Вейча для некторых функций, представимых двух­буквенными выражениями: а – функция x₁ x₂; б – функция 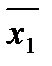x₃; в – функция 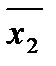x₃; г – функция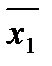 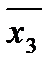; д – функция x₁ 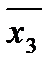; е – функция x₁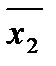

Четыре единицы, расположенные в соседних смежных клетках, выражаются од­ной буквой.

Рис. 2.6. Диаграммы Вейча для некоторых функций, представимых в виде

одной переменной: а – функция x₃; б – функция ; в – функция

Чтобы построить диаграмму Вейча функции, заданной в СДНФ, нужно записать единицы в клетки диаграммы, которые соответствуют консти­ту­ентам единицы данной функции.

Если функция задана в СКНФ, следует записать нули в клетки диа­грам­мы, которые соответствуют конституентам нуля, входящим в данную функ­цию, а в остальных клетках записать единицы.

Отыскание минимальной ДНФ сводится к определению варианта, при котором все единицы диаграммы Вейча данной функции накрываются наименьшим числом наиболее коротких произведений.

Пример 2.3.

f(x₁, x₂, x₃) = .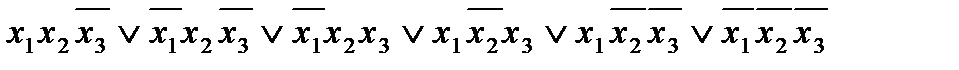

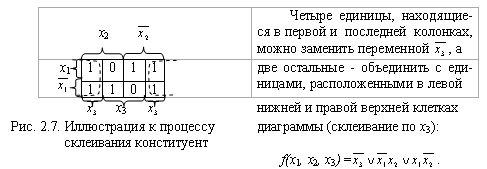
Данная функция имеет единственную минимальную форму, поскольку при любом другом способе объединения единиц количество букв в ДНФ уве­ли­чивается.

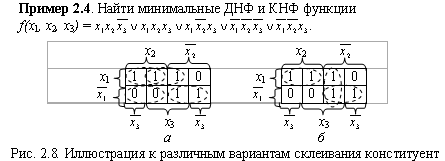
а - f(x₁, x₂, x₃) = x₁ x₂Ú x₁ x₃Ú 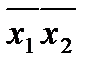; б - f(x₁, x₂, x₃) = x₁ x₂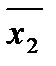Ú x₃Ú .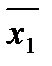

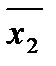Для получения минимальной КНФ следует объединить нули пере­клю­ча­тель­ной функции: две конституенты нуля соответствуют клеткам, объе­ди­ненным пунктиром, склеиваются по x₃ и представляются импликантой x₁Ú 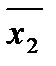, а оставшийся нуль – конституентой 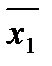Ú x₂Ú x₃. Поэтому минимальная КНФ будет иметь вид

f(x₁, x₂, x₃) = (x₁Ú 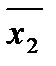)( 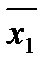Ú x₂Ú x₃).

Минимальная КНФ имеет меньше букв, чем минимальная ДНФ.

Пример 2.5. Найти минимальную ДНФ функции

f(x₁, x₂, x₃) = .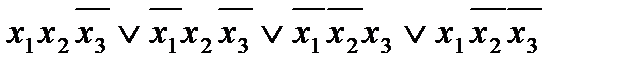

Рис. 2.9. Вариант склеивания конституент, приводящий к единственной минимальной ДНФ

Пример 2.6. Найти минимальную ДНФ функции

f(x₁, x₂, x₃) = .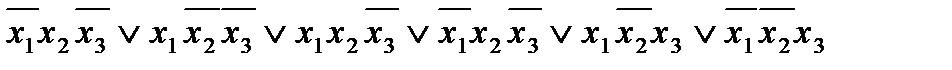

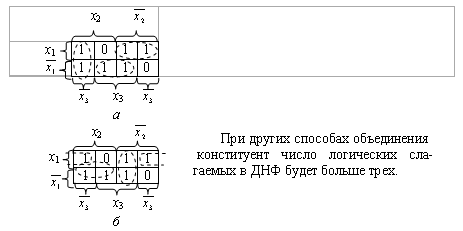
Рис. 2.10. Варианты склеивания конституент, приводящие к различным

минимальным ДНФ: а - f(x₁, x₂, x₃) = ;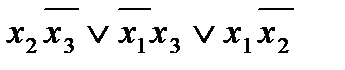

б - f(x₁, x₂, x₃) = .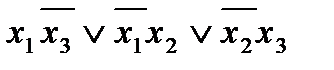

Пример 2.7. Найти минимальную ДНФ функции

f(x₁, x₂, x₃) = .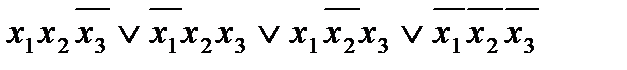

Рис. 2.11. Диаграмма Вейча для переключательной функции, у которой совершенная, сокращенная, тупиковая и минимальная формы совпадают

Диаграмма Вейча для функции четырех аргументов представляет собой квадрат, разделенный на 16 клеток.

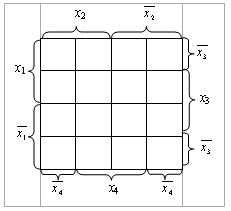
Рис. 2.12. Диаграмма Вейча для функции четырех переменных

Одной букве соответ­ству­ет восемь единиц, рас­по­ло­женных в соседних клет­ках; произведению, включаю­ще­му две переменные, соот­вет­ствуют че­тыре со­сед­ние еди­ницы; про­изведению трех пе­ре­мен­ных – две и произ­ве­дению че­тырех переменных – одна еди­ница.

Первую и последнюю колонки диаграммы, а также верхнюю и нижнюю строки следует считать соседними. Поэтому диаграмму Вейча для функций четырех аргументов следует представлять нанесенной на поверхность тора.

Пример 2.8.

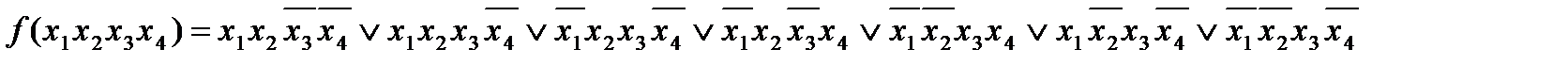
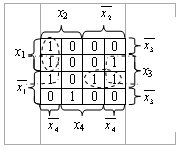
Рис. 2.13. Вариант склеивания конституент, приводящий к получению минимальной ДНФ

Диаграмма Вейча для функции пяти аргументов имеет следующий вид:

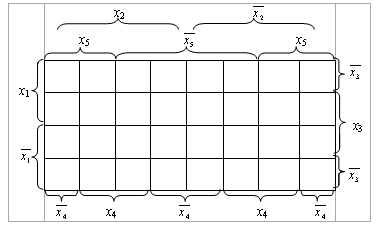
Рис. 2.14. Диаграмма Вейча для функций пяти переменных

Одной букве в этом случае соответствуют шестнадцать еди­ниц, рас­по­­ложенных в смежных клет­­­ках; произведе­нию двух букв – восемь еди­ниц, трех букв – че­тыре, четырех – две и пяти – одна единица.

Следует помнить, что для букв 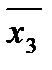, x₄, 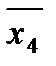и x₅ "соседние" клетки ока­зы­ваются разнесенными.

Аналогично строится диаграмма Вейча и для переключательных функ­ций большего числа аргументов. Однако с увеличением числа аргументов ра­бо­та с диаграммами затрудняется, поскольку теряется геометрический смысл "со­сед­них" клеток.