Представление переключательной функции в виде полинома Жегалкина.
Теорема Жегалкина. Любая переключательная функция может быть представлена в виде полинома (многочлена), т. е. записана в форме
f(x1, . . . , xn) = ао Å a1x1 Å a2x2 Å …Å anxn Å an+1x1 x2Å … Å aNx1…xn ,
(3.1)
где a0, a1x1, … aN— константы, равные нулю или единице;
Å —операция сложения по модулю два.
При записи конкретной переключательной функции в виде многочлена коэффициенты a0, a1x1, … aN выпадают, так как члены, при которых коэффициенты равны нулю, можно опустить, а коэффициенты, равные единице, не писать.
Для доказательства теоремы Жегалкина предположим, что задана произвольная переключательная функция п аргументов f(x1, . . . , xn), равная единице на некотором числе наборов с номерами m1, … mp.
Покажем, что переключательная функция f(x1, . . . , xn) равна сумме конституент единицы, которые равны единице на тех же наборах, что и данная функция:
f(x1, . . . , xn) = Km1 Å Km2 Å . . . Å Kmp. (3.2)
Действительно, на каждом из наборов с номерами m1, … mp равна единице только одна конституента, стоящая в правой части выражения (3.2), а остальные равны нулю. Следовательно, на этих наборах и только на них правая часть выражения (3.2) принимает значение, равное единице.
Для того чтобы перейти от выражения (3.2) к виду (3.1), достаточно представить конституенты единицы в виде произведений и, используя соотношение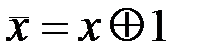 
, заменить все переменные с отрицаниями (так как отрицания в выражение (3.1) не входят). Пусть например, конституента единицы записана в виде
.
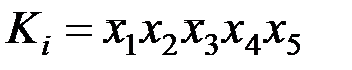Тогда получим
Ki= (1 Å x1)x2(1Åx3)x4x5.
Раскрывая скобки и приводя подобные члены в соответствии со свойствами операции сложения по модулю два, получаем запись заданной функции в форме (3.1), что и доказывает теорему.
Приведенное доказательство теоремы позволяет сформулировать правило представления любой переключательной функции в виде многочлена.
Чтобы переключательную функцию, заданную таблицей истинности, представить в виде полинома Жегалкина, достаточно записать функцию в виде суммы конституент единицы, равных единице на тех же наборах, на которых равна единице заданная функция. Затем все аргументы, входящие в полученное выражение с отрицанием, заменить с помощью соотношения 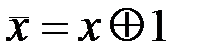, раскрыть скобки и привести подобные члены с учетом тождества:
x, если п нечетно,
x Å x Å . . . Å x =
0, если п четно.
Пример 3.3. Представить в виде полинома Жегалкина функцию f58(x1,x2,x3) (см. табл. 1.1).
Функция f58(x1,x2,x3) равна единице на втором, третьем, четвертом и шестом наборах, и может быть записана в виде суммы соответствующих конституент единицы:
f58(x1,x2,x3) =K2Å K3Å K4Å K6 =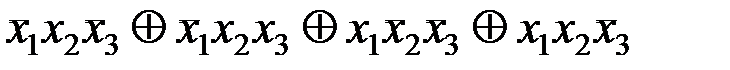 
.
Используя соотношение 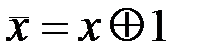, получаем
f58(x1,x2,x3)=(1Å x1)x2(1Å x3)Å (1Å x1)x2x3Å x1(1Å x2)(1Å x3)Å x1x2(1Å x3).
Приводя подобные члены, окончательно находим
f58(x1,x2,x3)= x1Å x2Å x1x2Å x1x3.