Протокол согласования учебной программы
ПО ИЗУЧАЕМОЙ УЧЕБНОЙ ДИСЦИПЛИНЕ
С ДРУГИМИ ДИСЦИПЛИНАМИ СПЕЦИАЛЬНОСТИ
(дисциплины, изучение которых опирается на данную дисциплину)
| Название дисциплины, с которой требуется согласование | Кафедра, обеспечивающая изучение этой дисциплины | Предложения об изменениях в содержании учебной программы по изучаемой дисциплине | Решение, принятое кафедрой, разработавшей учебную программу (с указанием даты и номера протокола)[1] |
| 1. Теория вероятностей и математическая статистика | Информатики | Нет | |
| 2. Имитационное и статистическое моделирование | Информатики | Нет | |
| 3. Архитектура вычислительных систем | Информатики | Нет |
Зав. кафедрой информатики Минченко Л.И.
ТЕОРЕТИЧЕСКИЙ РАЗДЕЛ
Лекции
ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
1.1 Основные понятия и определения
Будем рассматривать только функции конечного числа аргументов.
Рассмотрим множество векторов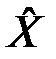 
={<x1, … , xn>}, координаты которых могут принимать лишь два значения - 0 или 1. Тогда множество 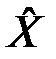состоит из 2n различных векторов. Сопоставим каждому вектору из 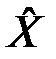символы 0 или 1, т.е. произведем однозначное отображение множества X на множество Y = {0,1}.
Определение 1.1.1. Функцией алгебры логики, или переключательной функцией, называется функция, дающая однозначное отображение 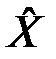в Y [1].
Из этого определения следует, что функция f(x1, … ,xn) называется переключательной, если она, так же как и ее аргументы, может принимать только значения из двухбуквенного алфавита, например, 0 и 1.
Поскольку аргументы переключательной функции могут принимать только два значения, то область определения любой переключательной функции конечна. Совокупность значений аргументов называется набором и обозначается a1, …, ai, …, an, где ai равно 0 или 1 (i = 1, …, n). Каждый набор может быть представлен n–разрядным двоичным числом, а количество двоичных n–разрядных чисел равно 2n. Поэтому любая переключательная функция может быть определена на 2n наборах.
Например, переключательные функции двух аргументов определены на четырех наборах (00, 01, 10, 11), а переключательные функции трех аргументов – на восьми. Таким образом, переключательная функция может быть задана таблицей, в которой перечислены все возможные значения аргументов функции (наборы) и соответствующие этим наборам значения функции. Такая таблица называется таблицей истинности переключательной функции. Пример переключательной функции трех аргументов приведен в табл. 1.1.
Таблица 1.1
Таблица значений переключательной функции
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| f(x1,x2,x3) |
Каждому набору аргументов можно приписать номер, равный двоичному числу, соответствующему данному набору:
0,0,0,0,0 — нулевой набор;
0,0,0,0,1 — первый набор;
. . . . . . . . . . . . . . . . . . . . . . .
1,1,1,1,1 — тридцать первый набор.
Набор, содержащий все единицы (1,1, …, 1), называют единичным набором.
Переключательная функция n аргументов определена на 2n наборах, на которых она может принимать значения 0 или 1. Поэтому в соответствие каждой переключательной функции можно поставить 2n-разрядное двоичное число. Количество 2n-разрядных двоичных чисел равно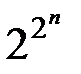 
. Таким образом, число различных переключательных функций n аргументов конечно и равно .
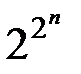Припишем каждой переключательной функции номер, равный двоичному числу, образованному значениями переключательной функции на всех наборах. Этот номер записывается слева направо, начиная со значения функции на нулевом наборе. Например, двоичное число, образованное значениями функции из табл. 1.1, 00111010(2), равно 58 в десятичной системе счисления и функцию можно обозначить следующим образом:
f(x1,x2,x3) = f58(x1,x2,x3).
Пример 1.1. Составить таблицу истинности для переключательной функции номер 23805 четырех аргументов.
Решение. Переключательная функция четырех аргументов определяется на 24 = 16 наборах (табл. 1.2) . Для получения значений функций представим число 23805 в двоичной системе счисления: 23805(10) =
= 101110011111101(2). Полученное двоичное число имеет 15 двоичных разрядов, и для представления переключательной функции необходимо дополнить полученный код до 16-разрядного: 0101110011111101.
Таблица 1.2
Таблица переключательной функции f23805(x1,x2,x3,x4)
| x1 | ||||||||||||||||
| x2 | ||||||||||||||||
| x3 | ||||||||||||||||
| x4 | ||||||||||||||||
| f23805(x1,x2,x3,x4) |
Определение 1.1.2. Если две переключательные функции f(x1, …, xn) и φ(x1, …, xn) одного и того же числа аргументов принимают на всех возможных наборах значений аргументов одинаковые значения, то функции f и φ называются равными.
Факт равенства функций f и φ записывается так:
f(x1, …, xn) = φ(x1, …, xn).
Определение 1.1.3. Переключательная функция f(x1, …xi-1,xi,xi+1, …, xn) существенно зависит от аргумента xi, если имеет место соотношение
f(x1, …xi-1, 0, xi+1, …, xn) ¹f(x1, …xi-1, 1, xi+1, …, xn).
В противном случае говорят, что от аргумента xi функция зависит несущественно и xi является ее фиктивным аргументом. Переключательная функция не изменится, если к ее аргументам дописать любое число фиктивных аргументов или зачеркнуть те аргументы, которые являются фиктивными.