Освобождают от опор и заменяют их действие на балку реакциями.
В задачах на балку действуют только вертикальные нагрузки и сосредоточенные моменты. Реакции опор при нагрузке будут только вертикальными. Обычно их направляют вверх (против действия основной нагрузки) и обозначают реакцию опор А - RА, В – RВ
4. Составляют уравнения равновесия вида:ΣМА = 0 , ΣМВ = 0
Напомним, что моментом силы относительно точки называется произведение этой силы на плечо – кратчайшее расстояние от этой точки приложения силы (в общем случае до линии действия силы).
Если сила стремится повернуть балку относительно рассматриваемой точки по часовой стрелке, то будем считать её момент положительным, а если против – отрицательным.
Сосредоточенный момент не умножается на расстояние до опоры, а правило знаков остаётся тем же, что для момента силы.
Выполняют проверку решения:Для этого составляют уравнение равновесия:
ΣFу= 0
Пример:Определить опорные реакции балки, изображённой на рисунке
Дано: g1 = 20 кН/м , g2 = 15 кН/м, М= 25 кНм, F=30 кН
| Рисунок g 1 g2 A B F 1м 3,5 м 1м 1,5м 1,5м 8,5 м |
Расчётная схема
RА Rв М
А В
G1 F G2
1 м 1,25м 2,25 м 1 м 1,5 м 1,5 м
Решение: 1. Заменяем распределённую нагрузку равнодействующей.На балку действуют нагрузки разной интенсивности, поэтому для каждой из них найдём равнодействующую.
G1 = g1 · 20 (1+3,5) = 90 кН, G2 = g2 · 15 (1,5+1,5) = 45 кН
2 Обозначим опоры А и В, Укажем опорные реакцииRА, Rв
3. Составляем уравнения равновесия:ΣМА = 0 , ΣМВ = 0
ΣМА = 0: G1 · 1,25 - F · 4,5 + G2 · 6 - Rв · 6 – М = 0
Rв · 6 = - G1 · 1,25 + F · 4,5 - G2 · 6 + М
Rв = - G1 · 1,25 + F · 4,5 - G2 · 6 + М / 6
Rв = 90 · 1,25 – 30 · 4,5 +45 · 6 – 25 / 6, Rв = 37,1 кН.
ΣМВ = 0: -М + F · 1,5 - G1 · 4,75 + RА · 6 = 0
RА · 6 = М - F · 1,5 + G1 · 4,75
RА = М - F · 1,5 + G1 · 4,75 / 6
RА = 25 - 30 · 1,5 + 90 · 4,75 / 6 RА = 67,9 кН.
5.Выполняем проверку, используя уравнениеΣFy= 0, которое примет вид
RА - G 1 + F + Rв - G2 = 0; 67,9 – 90 +30 +37,1 – 45 = 0
45 – 45 = 0; 0 = 0, реакции опор определены правильно.
Ответ: RА = 67,9 кН., Rв = 37,1 кН.
Задание Определить величины реакций в опорах балочных систем под действием сосредоточенных сил и распределенной нагрузки. Провести проверку правильности решения. Данные взять из таблицы 2, схема 2 - одноопорной балки (заделка) и таблицы 3, схема 3– для двухопорной балки с шарнирными опорами
Таблица 2
| Исходные данные | вариант | |||||||||
| № схемы | ||||||||||
| Угол α0 | ||||||||||
| a1,м | 0,7 | 2,5 | 0,7 | 2,0 | 1,7 | 0,8 | 1,2 | 1,2 | 0,5 | |
| a2,м | 0,8 | 0,6 | 0,5 | 4,5 | 0,3 | 2,2 | 1,2 | 0,8 | 1,3 | |
| a3,м | 1,5 | 0,8 | 0,7 | 0,5 | - | 1,2 | 1,5 | 2,6 | 2,5 | 2,2 |
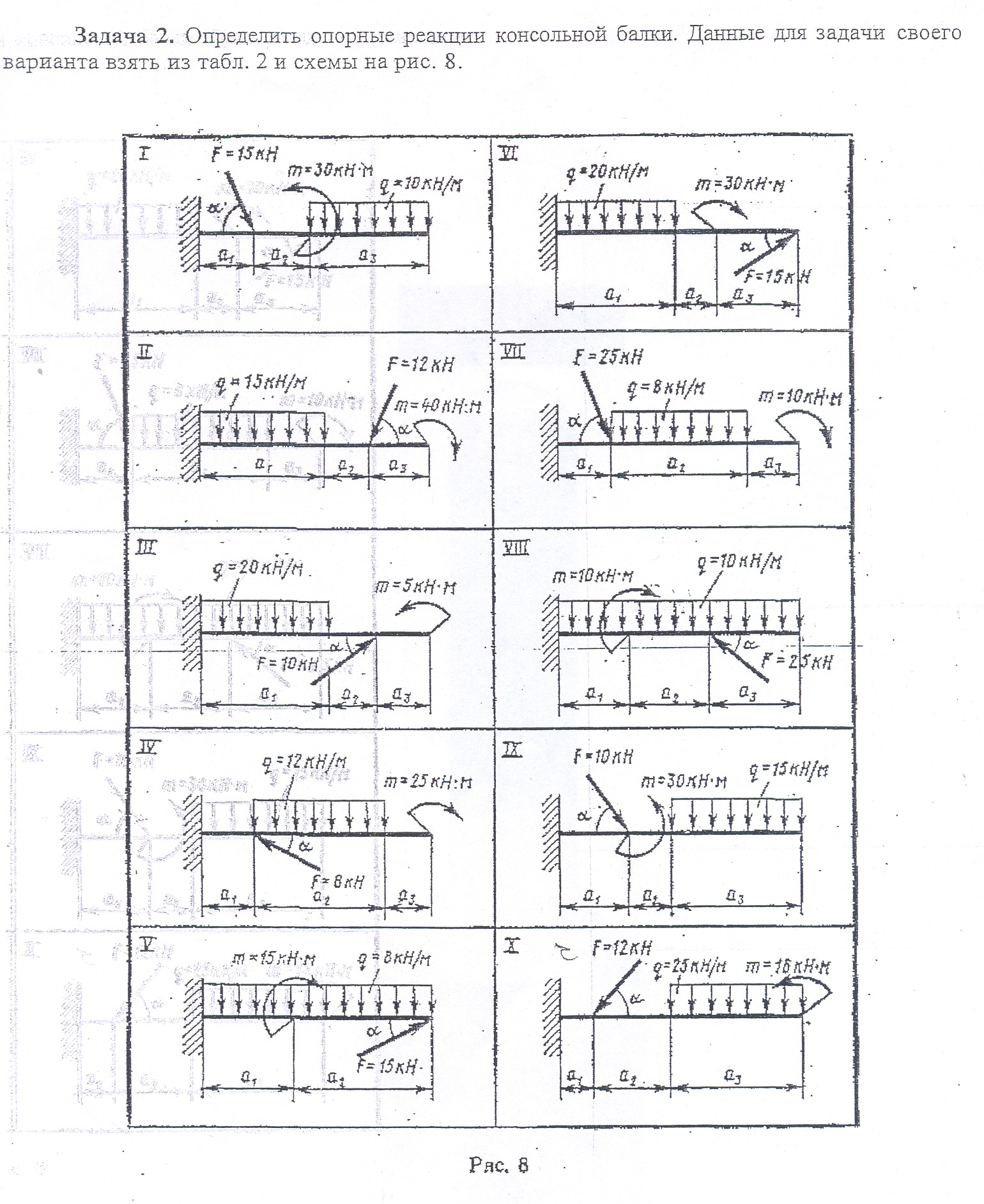Схема 2
Таблица 3
| Исходные данные | вариант | |||||||||
| № схемы | ||||||||||
| Угол α0 | ||||||||||
| a1,м | 1,2 | 2,5 | 1,5 | 3,0 | 1,2 | 1,1 | 1,2 | 1,5 | 1,8 | 1,5 |
| a2,м | 0,5 | 1,2 | 1,2 | 0,8 | 1,5 | 2,5 | 3,0 | 2,5 | 2,2 | 0,8 |
| a3,м | 0,8 | 0,8 | 2,5 | 1,2 | 1,5 | 0,7 | 0,5 | 1,5 | 0,7 | 1,5 |
| а4,м | 2,5 | 1,2 | - | - | 0,5 | 0,7 | 0,8 | - | - | 0,6 |
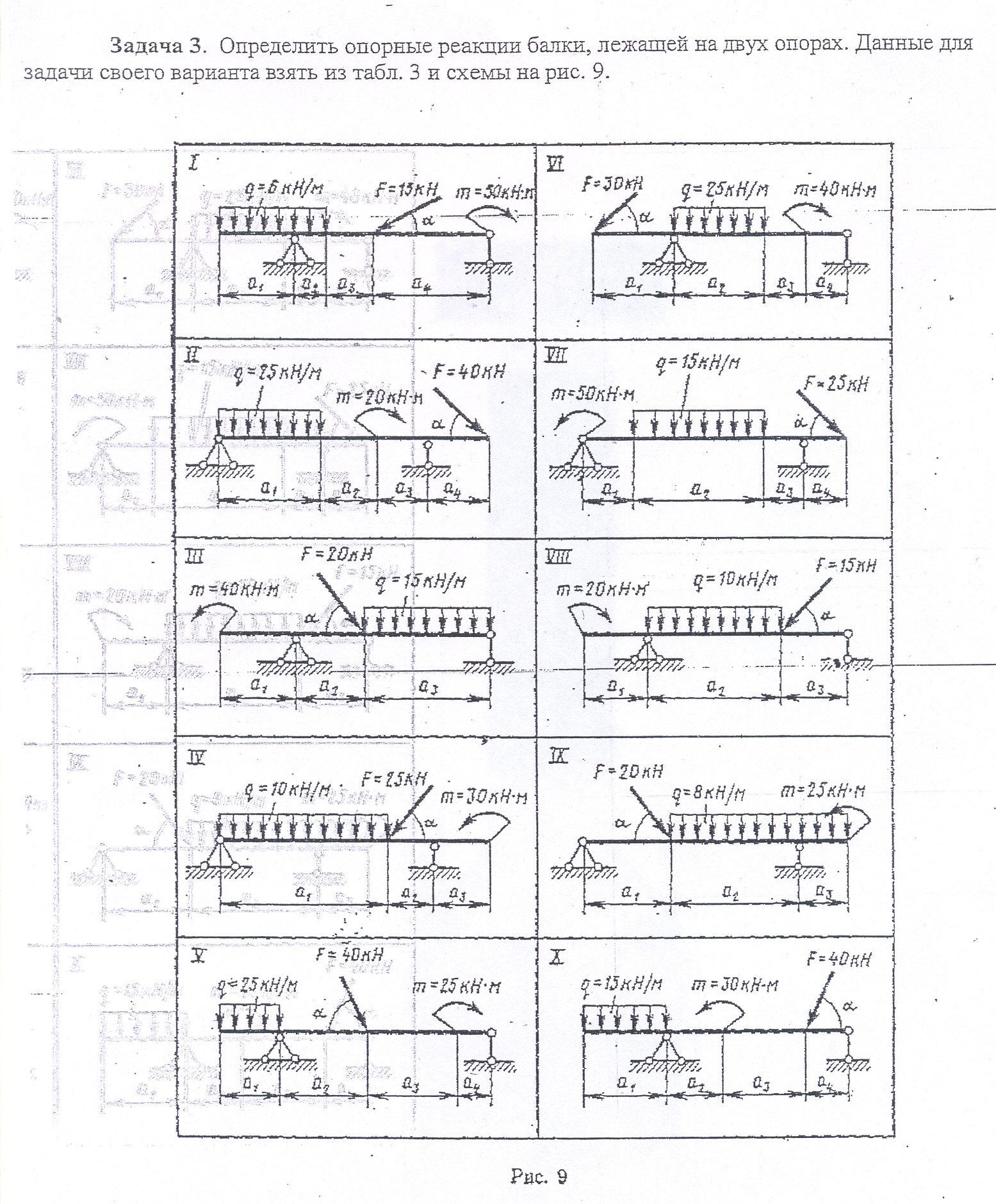Схема 3
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ |
| Разраб. |
| Провер. |
| . |
| Лит. |
| Листов |
| Группа_____________________ |
Оборудование (приборы, материалы, дидактическое обеспечение)________________________________________________________
Компьютерная программа (если используется): Наименование программы_________________________________________________________
| Рисунок: | Дано: _____________________________________ _____________________________________ _____________________________________ Определить реакции в заделке: ____________________________________ _____________________________________ |
| Расчётная схема: | 1 Выбираем объект, равновесие которого рассматриваем: балка Обозначаем опору А 2 Заменяем распределённую нагрузку её равнодействующей G = gℓ (если такая нагрузка имеется ) G =____________ 3 Освобождаем от опор и заменяем их действие на балку реакциями. |
| 4 Проанализируем, полученную систему сил. 5Выбираем систему координат - проводим оси «Х» и «У» 6 Составляем уравнения равновесия вида: ΣFx ΣFх = 0 , ΣFу = 0, ΣМА = 0 |
Решение уравнений:
Выполняем проверку решения:Для этого составляют уравнение равновесияотносительно мнимой точки (В)
ΣМ(В)=0
Вывод:_____________________________________________________________
|
| Дано: _____________________________________ _____________________________________ _____________________________________ Определить реакции в опорах: ____________________________________ _____________________________________ | ||||||||
| Расчётная схема: | 1 Выбираем объект, равновесие которого рассматриваем: балка Обозначаем опорыА-В 2 Заменяем распределённую нагрузку её равнодействующей G = gℓ (если такая нагрузка имеется ) G=_____________________________ 3 Освобождаем балку от опор и заменяем действие на балку реакциями. | ||||||||
| 4 Проанализируем, полученную систему сил. 5Выбираем систему координат - проводим оси «Х» и «У» 6 Составляем уравнения равновесия вида: ΣFx = 0 ΣFу = 0 , ΣМА = 0, ΣМВ = 0 |
| Решение уравнений |
Выполняем проверку решения:Для этого составляют уравнение равновесия:
ΣFу = 0
Вывод:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ |
1.Что называется плечом пары?_____________________________________________
________________________________________________________________________
________________________________________________________________________
2.Чтобы определить эффект действия пары сил, надо знать?_____________________
________________________________________________________________________
3.Пару сил можно уравновесить…?__________________________________________
________________________________________________________________________
4.Зависит ли величина и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы? ________________________________________________________________________________________________________________________________________________
5.Для чего используется рычаг?____________________________________________
_______________________________________________________________________
6.Какую из форм уравнений равновесия целесообразно использовать при определении реакций в заделке?_____________________________________________
________________________________________________________________________
7.Когда момент силы относительно точки положителен?_______________________
_______________________________________________________________________
8. Какую из форм уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?_________________________________________________________________
________________________________________________________________________________________________________________________________________________
9.Что вызывает пара сил?________________________________________________
______________________________________________________________________
10. Можно ли перемещать пару сил в плоскости ее действия?_______________________________________________________________
________________________________________________________________________________________________________________________________________________
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ИМПЕРАТОРА АЛЕКСАНДРА I»
(ФГБОУ ВПО ПГУПС)
ПЕТРОЗАВОДСКИЙ ФИЛИАЛ
Практическое занятие 3