Метод электромеханических аналогий

В примерах, рассмотренных выше, модель и оригинал имели одинаковую

физическую природу. Если же оригинал описывается той же системой уравнений, что и модель, но имеет иную физическую природу, то применяется математическое моделирование. В настоящее время широко известны аналогии механических, электрических, акустических, гидравлических, тепловых и других явлений и процессов.

Академик А.Н. Крылов писал: «Таких аналогий между вопросами совершенно разных областей, но приводящих к одинаковым дифференциальным уравнениям, можно привести множество. Казалось бы, что может быть общего между движением небесных светил под действием притяжения к Солнцу и между собой и качкой корабля на волнении или между определением, так называемых вековых неравенств в движении небесных тел и крутильными колебаниями вала многоцилиндрового двигателя Дизеля, работающего на корабельный винт или электрогенератор, между тем, если написать только формулу и уравнение без слов, то нельзя отличить, какой из этих вопросов решается: уравнение одни и те же.

При математическом моделировании основой соотношения модель – натура является такое обобщение теории подобия, которое учитывает качественную разнородность модели и натуры, принадлежность их к разным формам движения материи. Такое обобщение принимает форму более абстрактной теории изоморфизма систем. Основой такого подхода является аналогия – правдоподобное и вероятное заключение о сходстве двух предметов или явлений в каком-либо признаке на основании установленного их сходства в других признаках. Принцип математической аналогии позволяет экспериментально находить решение дифференциальных уравнений на модели в той области, где эксперимент осуществляется наиболее легко и точно. Трудно найти более подходящую для этой цели область техники, чем электротехника. Необходимые для этой цели элементы электрических цепей (емкости, индуктивности и резисторы) портативны, дешевы и могут быть выполнены просто и с большой степенью точности, а электроизмерительные приборы обладают высокой точностью измерений.

В 1881 г. Максвелл изложил языком механики Лагранжа теорию электромагнитных явлений, приняв в качестве обобщенной величины перемещения электрический заряд, в качестве обобщенной скорости – силу тока и в качестве механической силы – величину электродвижущей силы.

Электрическое моделирование механических систем производится при физической постановке задачи, когда механическая система характеризуется массой, упругостью, трением и связями. По этой ее физической характеристике и строится модель-схема, в которой все элементы заменены аналогичными.

Электрическое моделирование возможно при математической постановке задачи. В этом случае сначала составляется дифференциальное уравнение исследуемой механической системы и для его решения создается электрическая, характеризуемая точно таким же дифференциальным уравнением – математическая модель.

В настоящее время результатом развития электрического моделирования явилось создание двух систем электромеханических аналогий.

Эти системы установлены путем сопоставления уравнений поступательного и вращательного движений механической системы и уравнений для электрической цепи, состоящей из индуктивности, емкости и активного сопротивления, соединенных последовательно и параллельно.

Уравнения поступательного и вращательного движений механической системы имеют вид

. (6.1)

, (6.2)

где – масса;

– перемещение;

– сопротивления трению соответственно при поступательном и вращательном движениях;

– коэффициенты, учитывающие упругие свойства пружины, т.е. жесткость соответственно при сжатии (растяжении) и закручивании (раскручивании);

– момент инерции;

– угол поворота (закручивания);

– механический момент;

– механическая сила.

При последовательном соединении индуктивности, активного сопротивления и емкости уравнение электрического состояния цепи согласно второму закону Кирхгофа можно представить в виде

, (6.3)

где – индуктивность;

– емкость;

– активное сопротивление;

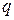– электрический заряд;

– электрическое напряжение.

При параллельном соединении этих элементов согласно первому закону Кирхгофа получим

, (6.4)

где – магнитный поток;

– сила электрического тока.

В уравнениях (6.1) и (6.2) слагаемые представляют собой силы, действующие соответственно на сосредоточенную массу, элемент сопротивления (демпфер), элемент упругости (пружину) или моменты, действующие на аналогичные элементы при вращательном движении механической системы.

В уравнении (6.3) слагаемые представляют собой напряжения на индуктивности, емкости и активном сопротивлении при последовательном их соединении.

В уравнении (6.4) слагаемые представляют собой токи в ветвях цепи с параллельным соединением емкости, активного сопротивления и индуктивности.

Физической основой механической системы являются законы Кирхгофа. Каждому уравнению равновесия сил в механической системе соответствует уравнение балансов напряжений цепи с последовательным соединением

или уравнение токов для отдельного узла с параллельным соединением:

(6.5)

(6.6)

(6.7)

Механические параметры системы и соответствующие им электрические величины приведены в табл.6.1. При изучении физико-механических свойств горных пород используются механические системы, представляющие собой всевозможные комбинации, составленные из идеальных сред: Гука, Ньютона и Сен-Венана.

Таблица 6.1

Характер величин	Механическая система	Электрическая система
Поступательное движение	Вращательное движение	I система аналогий	II система аналогий
Параметры системы	Инертная характеристика	Индуктивность	Емкость
Сопротивление трению	Омическое сопротивление	Проводимость
Податливость	Емкость	Индуктивность
Параметры состо-яния	Перемещение	Заряд	Потокосцепление Напряжение
Скорость	Ток	Напряжение
Усилие	Напряжение	Ток
Энергия	Кинетическая энергия	Магнитная энергия	Электрическая энергия
Потенциальная энергия	Электрическая энергия	Магнитная энергия
Рассе-яние энергии

Таким образом, можно считать, что электрический заряд соответствует относительной деформации , сила тока – скорости деформации ; электрическое напряжение – напряжению в образе горной породы .

Упругие, вязкие и пластические свойства горных пород могут быть представлены механическими и электрическими моделями.

1. Упругость. Твердые тела, при механическом нагружении которых наблюдается линейная зависимость между напряжением и деформацией, называют телами Гука. Механической моделью такого тела является пружина. Деформации тела упруги (при снятии нагрузки полностью восстанавливается равновесное состояние) и определяются приложенной силой и тяжестью пружины

, (6.8)

где – приложенная к пружине сила;

– коэффициент, учитывающий жесткость пружины;

– деформация пружины.

Зависимость между напряжением и деформацией (для случая упругой деформации) выражается законом Гука:

, (6.9)

где – напряжение, Н/м²;

– относительная деформация.

Идентичность зависимостей (6.8) и (6.9) послужила причиной тому, что упругие свойства горных пород в механических моделях аппроксимируется пружиной.

В качестве электрического анализа упругих свойств горных пород может служить емкость, для которой справедливо выражение

, (6.10)

где – приложенное напряжение, В;

– емкость конденсатора, Ф;

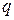– заряд на обкладках конденсатора, Кл.

Энергия, накопленная электрическим полем,

, (6.11)

полностью возвращается источнику при разряде конденсатора.

Потенциальная энергия упругой деформации, запасенная в единице объема деформируемого тела,

, (6.12)

полностью возвращается при исчезновении возмущающей силы.

Вязкость.

Механической моделью, характеризующей свойства вязкости твердого тела, является тело Ньютона ( – тело). Напряжения в нем прямо пропорциональны скорости деформирования

, (6.13)

где – вязкость среды, Н.с/м²;

– скорость деформирования, с^-1;

– напряжение, Н/м².

Элемент, отражающий поведение такого тела при нагружении, представляется в виде поршня с отверстиями, движущегося в цилиндре, наполненном вязкой жидкостью.

Аналогом вязких свойств горных пород при электрическом моделировании может служить омическое сопротивление.

Величина падения напряжения на сопротивлении определяется уравнением

, (6.14)

где – напряжение на сопротивлении, В;

– величина омического сопротивления, Ом;

– сила электротока, А.

Известно, что процесс деформации жидкости необратим и энергия не

может быть накоплена в теле или возвращена им.

Затраченная в таком необратимом процессе работа полностью рассеивается – переходит в тепло.

Энергия электрического тока выделяется в виде тепла в омическом сопротивлении.

Пластичность.

Особенность пластического течения состоит в том, что оно возникает в твердом теле под действием напряжений, превосходящих определенное критическое значение и прекращается тогда, когда напряжения становятся меньше этого критического значения.

Элементарной моделью, отражающей пластическую деформацию при нагружении, является модель сухого трения лежащего на горизонтальном основании массивного тела, сдвигаемого внешними силами.

Смещение его возможно лишь при достижении внешним усилием определенной величины. При равенстве сил трения покоя и внешних сил начинается перемещение тела, причем для поддержания движения тела достаточно приложить силу, меньшую силы трения покоя, т.е.

< . (6.15)

Тело, деформируемое по такому закону, называется средой Сен-Венана ( -тело). Механической моделью этого тела будет груз, лежащий на горизонтальном основании, последовательно соединенный с пружиной.

В качестве электрического аналога этой механической модели может быть двухэлектродный ионный прибор (неоновая лампа).

Если на электроны неоновой лампы подать напряжение, то до тех пор, пока оно будет оставаться меньше напряжения зажигания лампы, ток в цепи лампы практически проходить не будет.

При достижении равенства разности потенциалов между электродами лампы величины за счет ударной ионизации газа внутри лампы ее внутреннее сопротивление резко снижается и между электродами происходит раз-

ряд, сопровождающийся свечением.

Для поддержания разряда достаточно приложить напряжение, несколько меньшее величины . Так же, как и в механической модели, вся энергия, расходуемая источником тока на поддержание разряда в межэлектродном пространстве, носит необратимый характер и полностью диссипируется.

4. Инерционность. В качестве инерционного элемента в механических моделях используется материальная точка, имеющая массу и обладающая абсолютной жесткостью.

В соответствии со вторым законом механики инерционная сила может быть выражена:

, (6.16)

где – масса, кг;

– перемещение, м;

– скорость, м/с.

Напряжения, вызванные силами инерции, можно выразить:

, (6.17)

где – приведенная масса, определяемая произведением плотности горной породы на площадь взаимодействия;

– относительная деформация, вычисляемая как относительное перемещение центра масс системы.

В электрических цепях мерой инерции является индуктивность цепи. Для цепи с индуктивностью справедливо равенство

, (6.18)

где – индуктивность, Гн;

– напряжение, В;

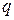– заряд, Кл;

– сила тока, А.

Следовательно, для механических моделей можно составить дифференциальные уравнения напряженного состояния горных пород, решение которых возможно на электрических моделях.

Действительно, поведение вязко-упругого тела при его нагружении можно объяснить с помощью механической модели, получившей название среды Кельвина-Фойгта.

Идеально упругая пружина и демпфер соединены в жесткую систему, находящуюся под напряжением (рис.6.1, а).

Для такой механической системы может быть построена (по первой системе аналогий) электрическая модель, представляющая собой электрическую цепь с последовательным соединением активного сопротивления и емкости (рис.6.1, б).

Пусть модуль упругости рассматриваемого вязко-упругого тела равен жесткости пружины, а коэффициент вязкого тела равен коэффициенту вязкости, в которой перемещается поршень. Тогда растягивающая сила будет уравновешиваться сопротивлением пружины и сопротивлением жидкости . При этом – изменение расстояния между точками А и Б системы.

Отождествляя силу с напряжением в материале, а перемещение – с его деформацией, можно получить зависимость между напряжением и деформацией в вязко-упругом теле:

. (6.19)

Закон изменения деформации при растяжении вязко-упругого тела постоянной силой можно найти, решив дифференциальное уравнение (6.19) и приняв в нем , а при , решением его будет

, (6.20)

где – время релаксации.

Из формулы (304) следует, что деформация вязко-упругого тела остается все время меньше деформации

, (6.21)

которая соответствует упругой деформации. Она достигает этой величины при , т.е. кривая деформаций имеет асимптоту (рис.6.1, а). После снятия напряжений в момент . можно получить закон изменения деформаций при
> .

Для этого в уравнении (6.19) следует положить и решить его, считая что при

, (6.22)

то есть . (6.23)

Таким образом,

(6.24)

или . (6.25)

Уравнение (6.25) представляет собой закон изменения деформаций в вязко-упругом теле при сжатии нагрузки.

Аналогично можно определить величину заряда конденсатора в цепи с

последовательным соединением активного сопротивления в емкости. Согласно второму закону Кирхгофа приложенное напряжение

. (6.26)

Напряжение на конденсаторе

, (6.27)

а ток в цепи есть скорость изменения заряда на обкладках конденсатора, т.е.

. (6.28)

Тогда уравнение (6.26) можно представить в виде

. (6.29)

Сравнивая уравнения (6.19) и (6.26), можно заключить, что зависимость между напряжением в вязко-упругом теле и зависимость между электрическим напряжением и величиной заряда описывается аналогичными уравнениями.

Закон изменения заряда конденсатора при включении его через сопротивление на постоянное напряжение, можно определить решением дифференциального уравнения (6.29).

Решением этого уравнения будет:

, (6.30)

где – постоянная времени. Из уравнения (6.30) следует, что величина заряда конденсатора изменяется по экспоненциальному закону от нуля при , асимптотически приближаясь к

или , (6.31)

где – напряжение источника.

Сравнив уравнения (6.20) с (6.30) и (6.21) с (6.31) нетрудно заметить соответствие (аналогично) процессов, происходящих в вязко-упругом теле, и процессов, происходящих в электрических цепях с последовательным соединением активного сопротивления и емкости.

Для определения закона изменения заряда при > , необходимо в уравнении (6.20) принять (разряд конденсатора) и решить его, считая, что :

, (6.32)

то есть . (6.33)

Решением дифференциального уравнения (6.33) будет

. (6.34)

На основании полученных выражений (6.25) и (6.34) можно заключить, что процессы, происходящие в вязком упругом теле после снятия напряжений, аналогичны процессам, происходящим в цепи с последовательным соединением активного сопротивления и емкости при заряде конденсатора (рис. 6.2, б).

При постоянных деформациях твердого тела напряжения будут постепенно уменьшаться. Явление уменьшения напряжения в теле при постоянных деформациях называется релаксацией напряжений. Это явление можно объяснить, рассмотрев механическую систему, называемую средой Максвелла (рис. 24, а).

	Рис.6.2. Сопоставление механической и электрической моделей в режиме релаксации напряжений: а – механическая модель среды Максвелла и релаксация в ней напряжений при фиксированной начальной деформации; б – электрический аналог модели Максвелла и изменение напряжения на конденсаторе при фиксированном начальном заряде на его обкладках.

Упругая пружина и демпфер соединены в податливую систему последовательно и находятся под напряжением .

Скорость продольной деформации системы складывается из скорости деформации пружины

(6.35)

и скорости деформации демпфера

(6.36)

Так как деформация пружины связана с напряжением законом Гука, то

. (6.37)

Деформация демпфера связана с напряжением и коэффициентом вязкости соотношением

. (6.38)

Следовательно, скорость деформации системы

. (6.39)

Уравнение (6.39) упрощенно объясняет явление релаксации напряжений в теле, характеристики которого соответствуют свойствам рассматриваемой системы.

В электрической цепи (рис.6.2, б) ток, протекающий в ветви с емкостью

. (6.40)

Ток, протекающий в ветви с активным сопротивлением

. (6.41)

Ток в неразветвленной части цепи согласно первому закону Кирхгофа

(6.42)

так как

, (6.43)

то

(6.44)

и, следовательно, ток в неразветвленной части цепи или скорость изменения заряда

. (6.45)

Установленная аналогия между упругими, вязкими и пластическими параметрами горных пород и соответствующими им элементами электрических цепей, а также идентичность процессов, протекающих в механических и электрических моделях, позволяет обобщить эти закономерности.