Моделирование тепловых процессов в горном деле
Моделирование гидродинамических процессов
Рассмотрим подобие стационарного течения несжимаемой вязкой жидкости для следующих случаев:
– при наличии влияния веса;
– при отсутствии влияния веса;
– вязкостное и инерционное течение.
Последние три вида течения являются частными случаями первого.
Вязкостный режим течения.
Вязкостный режим течения характеризуется исчезающе малым влиянием инерционных сил по сравнению с силами трения и давления. В этом случае на основании анализа уравнений:
движения
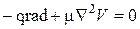 ;
;
сплошности
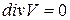 ;
;
граничных условий
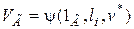 ,
,
где 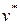 – параметрическое значение скорости,
– параметрическое значение скорости,
получается одно уравнение связи
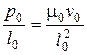 , (4.115)
, (4.115)
на основании которого устанавливается подобие двух потоков.
Для осуществления подобия необходимо выполнить равенство критериев 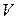 на границах потоков в модели и в образце, т.е.
на границах потоков в модели и в образце, т.е.
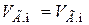 или
или 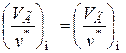 .
.
Отсюда видно, что подобие может быть осуществлено независимо от размеров модели.
Инерционный режим течения. В этом случае влиянием сил трения, ввиду их малости по сравнению с силами давления и инерции, на режим течения можно пренебречь.
Тогда после приведения уравнений:
движения
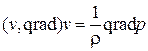 ;
;
сплошности
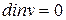 ;
;
граничных условий
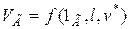
и безразмерному виду получим уравнение связи
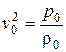 . (4.116)
. (4.116)
Следовательно, для установления подобия между двумя потоками необходимо выполнить то же условие, что и при вязкостном режиме, т.е.
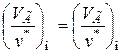 .
.
В данном случае подобие может быть осуществлено, так же как при вязкостном режиме, независимо от размеров модели, которая. разумеется, должна быть геометрически подобна образцу.
Сопоставим условия, необходимые для осуществления подобия в рассматриваемых задачах:
при наличии сил тяжести:
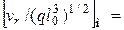
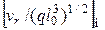 ;
;
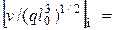
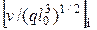 ;
;
при напорном течении
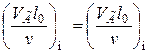 ;
;
при вязкостном течении
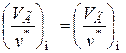 ;
;
при инерционном течении
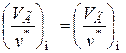 .
.
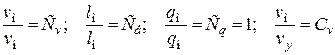 ,
,
получим при наличии влияния сил тяжести
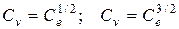 ;
;
при напорном течении
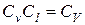 ;
;
при вязкостном и инерционном течении
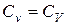 .
.
Следовательно, для первых двух режимов имеем ограничения в выборе множителей подобия. Действительно, выбрав в первом случае множитель геометрического подобия 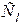 , мы тем самым предопределяем множители подобия
, мы тем самым предопределяем множители подобия 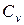 и
и 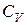 . Аналогично и в случае напорного течения.
. Аналогично и в случае напорного течения.
В противоположность рассмотренным двум первым видам течения, при осуществлении подобия вязкости и инерционного течения мы свободны в выборе множителей подобия. В последних двух случаях подобие обеспечивается одним лишь подобием распределения скоростей. Это свойство инерционного и вязкостного режимов течения называется автомоделью. При этом для вязкостного режима имеет место
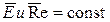 ,
,
а для инерционного режима
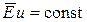 .
.
Вязкостный режим наблюдается в области малых значений числа 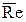 , а инерционный – в области больших значений числа
, а инерционный – в области больших значений числа 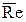 . В соответствии с этим принято говорить о первой и второй автомодельных областях. Значение автомодельности для практики моделирования совершенно очевидно, так как оно позволяет осуществить подобие на модели любых размеров с использованием любой рабочей жидкости.
. В соответствии с этим принято говорить о первой и второй автомодельных областях. Значение автомодельности для практики моделирования совершенно очевидно, так как оно позволяет осуществить подобие на модели любых размеров с использованием любой рабочей жидкости.
Вязкость.
Механической моделью, характеризующей свойства вязкости твердого тела, является тело Ньютона (  – тело). Напряжения в нем прямо пропорциональны скорости деформирования
– тело). Напряжения в нем прямо пропорциональны скорости деформирования
 , (6.13)
, (6.13)
где  – вязкость среды, Н.с/м2;
– вязкость среды, Н.с/м2;
 – скорость деформирования, с-1;
– скорость деформирования, с-1;
 – напряжение, Н/м2.
– напряжение, Н/м2.
Элемент, отражающий поведение такого тела при нагружении, представляется в виде поршня с отверстиями, движущегося в цилиндре, наполненном вязкой жидкостью.
Аналогом вязких свойств горных пород при электрическом моделировании может служить омическое сопротивление.
Величина падения напряжения на сопротивлении определяется уравнением
 , (6.14)
, (6.14)
где  – напряжение на сопротивлении, В;
– напряжение на сопротивлении, В;
 – величина омического сопротивления, Ом;
– величина омического сопротивления, Ом;
 – сила электротока, А.
– сила электротока, А.
Известно, что процесс деформации жидкости необратим и энергия не
может быть накоплена в теле или возвращена им.
Затраченная в таком необратимом процессе работа полностью рассеивается – переходит в тепло.
Энергия электрического тока выделяется в виде тепла в омическом сопротивлении.
Пластичность.
Особенность пластического течения состоит в том, что оно возникает в твердом теле под действием напряжений, превосходящих определенное критическое значение и прекращается тогда, когда напряжения становятся меньше этого критического значения.
Элементарной моделью, отражающей пластическую деформацию при нагружении, является модель сухого трения лежащего на горизонтальном основании массивного тела, сдвигаемого внешними силами.
Смещение его возможно лишь при достижении внешним усилием определенной величины. При равенстве сил трения покоя и внешних сил начинается перемещение тела, причем для поддержания движения тела достаточно приложить силу, меньшую силы трения покоя, т.е.
 <
<  . (6.15)
. (6.15)
Тело, деформируемое по такому закону, называется средой Сен-Венана (  -тело). Механической моделью этого тела будет груз, лежащий на горизонтальном основании, последовательно соединенный с пружиной.
-тело). Механической моделью этого тела будет груз, лежащий на горизонтальном основании, последовательно соединенный с пружиной.
В качестве электрического аналога этой механической модели может быть двухэлектродный ионный прибор (неоновая лампа).
Если на электроны неоновой лампы подать напряжение, то до тех пор, пока оно будет оставаться меньше напряжения зажигания лампы, ток в цепи лампы практически проходить не будет.
При достижении равенства разности потенциалов между электродами лампы величины  за счет ударной ионизации газа внутри лампы ее внутреннее сопротивление резко снижается и между электродами происходит раз-
за счет ударной ионизации газа внутри лампы ее внутреннее сопротивление резко снижается и между электродами происходит раз-
ряд, сопровождающийся свечением.
Для поддержания разряда достаточно приложить напряжение, несколько меньшее величины  . Так же, как и в механической модели, вся энергия, расходуемая источником тока на поддержание разряда в межэлектродном пространстве, носит необратимый характер и полностью диссипируется.
. Так же, как и в механической модели, вся энергия, расходуемая источником тока на поддержание разряда в межэлектродном пространстве, носит необратимый характер и полностью диссипируется.
4. Инерционность. В качестве инерционного элемента в механических моделях используется материальная точка, имеющая массу и обладающая абсолютной жесткостью.
В соответствии со вторым законом механики инерционная сила может быть выражена:
 , (6.16)
, (6.16)
где  – масса, кг;
– масса, кг;
 – перемещение, м;
– перемещение, м;
 – скорость, м/с.
– скорость, м/с.
Напряжения, вызванные силами инерции, можно выразить:
 , (6.17)
, (6.17)
где  – приведенная масса, определяемая произведением плотности горной породы на площадь взаимодействия;
– приведенная масса, определяемая произведением плотности горной породы на площадь взаимодействия;
 – относительная деформация, вычисляемая как относительное перемещение центра масс системы.
– относительная деформация, вычисляемая как относительное перемещение центра масс системы.
В электрических цепях мерой инерции является индуктивность цепи. Для цепи с индуктивностью справедливо равенство
 , (6.18)
, (6.18)
где  – индуктивность, Гн;
– индуктивность, Гн;
 – напряжение, В;
– напряжение, В;
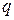 – заряд, Кл;
– заряд, Кл;
 – сила тока, А.
– сила тока, А.
Следовательно, для механических моделей можно составить дифференциальные уравнения напряженного состояния горных пород, решение которых возможно на электрических моделях.
Действительно, поведение вязко-упругого тела при его нагружении можно объяснить с помощью механической модели, получившей название среды Кельвина-Фойгта.
Идеально упругая пружина  и демпфер
и демпфер  соединены в жесткую систему, находящуюся под напряжением
соединены в жесткую систему, находящуюся под напряжением  (рис.6.1, а).
(рис.6.1, а).
Для такой механической системы может быть построена (по первой системе аналогий) электрическая модель, представляющая собой электрическую цепь с последовательным соединением активного сопротивления и емкости (рис.6.1, б).

Пусть модуль упругости рассматриваемого вязко-упругого тела  равен жесткости пружины, а коэффициент вязкого тела
равен жесткости пружины, а коэффициент вязкого тела  равен коэффициенту вязкости, в которой перемещается поршень. Тогда растягивающая сила
равен коэффициенту вязкости, в которой перемещается поршень. Тогда растягивающая сила  будет уравновешиваться сопротивлением пружины
будет уравновешиваться сопротивлением пружины  и сопротивлением жидкости
и сопротивлением жидкости  . При этом
. При этом  – изменение расстояния между точками А и Б системы.
– изменение расстояния между точками А и Б системы.
Отождествляя силу  с напряжением в материале, а перемещение – с его деформацией, можно получить зависимость между напряжением и деформацией в вязко-упругом теле:
с напряжением в материале, а перемещение – с его деформацией, можно получить зависимость между напряжением и деформацией в вязко-упругом теле:
 . (6.19)
. (6.19)
Закон изменения деформации при растяжении вязко-упругого тела постоянной силой можно найти, решив дифференциальное уравнение (6.19) и приняв в нем  , а при
, а при  , решением его будет
, решением его будет
 , (6.20)
, (6.20)
где  – время релаксации.
– время релаксации.
Из формулы (304) следует, что деформация вязко-упругого тела остается все время меньше деформации
 , (6.21)
, (6.21)
которая соответствует упругой деформации. Она достигает этой величины при  , т.е. кривая деформаций имеет асимптоту
, т.е. кривая деформаций имеет асимптоту  (рис.6.1, а). После снятия напряжений в момент
(рис.6.1, а). После снятия напряжений в момент  . можно получить закон изменения деформаций при
. можно получить закон изменения деформаций при
 >
>  .
.
Для этого в уравнении (6.19) следует положить 
 и решить его, считая что при
и решить его, считая что при 
 , (6.22)
, (6.22)
то есть  . (6.23)
. (6.23)
Таким образом,
 (6.24)
(6.24)
или  . (6.25)
. (6.25)
Уравнение (6.25) представляет собой закон изменения деформаций в вязко-упругом теле при сжатии нагрузки.
Аналогично можно определить величину заряда конденсатора в цепи с
последовательным соединением активного сопротивления в емкости. Согласно второму закону Кирхгофа приложенное напряжение
 . (6.26)
. (6.26)
Напряжение на конденсаторе
 , (6.27)
, (6.27)
а ток в цепи есть скорость изменения заряда на обкладках конденсатора, т.е.
 . (6.28)
. (6.28)
Тогда уравнение (6.26) можно представить в виде
 . (6.29)
. (6.29)
Сравнивая уравнения (6.19) и (6.26), можно заключить, что зависимость между напряжением в вязко-упругом теле и зависимость между электрическим напряжением и величиной заряда описывается аналогичными уравнениями.
Закон изменения заряда  конденсатора при включении его через сопротивление на постоянное напряжение, можно определить решением дифференциального уравнения (6.29).
конденсатора при включении его через сопротивление на постоянное напряжение, можно определить решением дифференциального уравнения (6.29).
Решением этого уравнения будет:
 , (6.30)
, (6.30)
где  – постоянная времени. Из уравнения (6.30) следует, что величина заряда конденсатора изменяется по экспоненциальному закону от нуля при
– постоянная времени. Из уравнения (6.30) следует, что величина заряда конденсатора изменяется по экспоненциальному закону от нуля при  , асимптотически приближаясь к
, асимптотически приближаясь к
 или
или  , (6.31)
, (6.31)
где  – напряжение источника.
– напряжение источника.
Сравнив уравнения (6.20) с (6.30) и (6.21) с (6.31) нетрудно заметить соответствие (аналогично) процессов, происходящих в вязко-упругом теле, и процессов, происходящих в электрических цепях с последовательным соединением активного сопротивления и емкости.
Для определения закона изменения заряда при  >
>  , необходимо в уравнении (6.20) принять
, необходимо в уравнении (6.20) принять  (разряд конденсатора) и решить его, считая, что
(разряд конденсатора) и решить его, считая, что  :
:
 , (6.32)
, (6.32)
то есть  . (6.33)
. (6.33)
Решением дифференциального уравнения (6.33) будет
 . (6.34)
. (6.34)
На основании полученных выражений (6.25) и (6.34) можно заключить, что процессы, происходящие в вязком упругом теле после снятия напряжений, аналогичны процессам, происходящим в цепи с последовательным соединением активного сопротивления и емкости при заряде конденсатора (рис. 6.2, б).
 При постоянных деформациях твердого тела напряжения будут постепенно уменьшаться. Явление уменьшения напряжения в теле при постоянных деформациях называется релаксацией напряжений. Это явление можно объяснить, рассмотрев механическую систему, называемую средой Максвелла (рис. 24, а).
При постоянных деформациях твердого тела напряжения будут постепенно уменьшаться. Явление уменьшения напряжения в теле при постоянных деформациях называется релаксацией напряжений. Это явление можно объяснить, рассмотрев механическую систему, называемую средой Максвелла (рис. 24, а).

|
Упругая пружина  и демпфер
и демпфер  соединены в податливую систему последовательно и находятся под напряжением
соединены в податливую систему последовательно и находятся под напряжением  .
.
Скорость продольной деформации системы складывается из скорости деформации пружины
 (6.35)
(6.35)
и скорости деформации демпфера
 (6.36)
(6.36)
Так как деформация пружины связана с напряжением законом Гука, то
 . (6.37)
. (6.37)
Деформация демпфера связана с напряжением  и коэффициентом вязкости соотношением
и коэффициентом вязкости соотношением
 . (6.38)
. (6.38)
Следовательно, скорость деформации системы
 . (6.39)
. (6.39)
Уравнение (6.39) упрощенно объясняет явление релаксации напряжений в теле, характеристики которого соответствуют свойствам рассматриваемой системы.
В электрической цепи (рис.6.2, б) ток, протекающий в ветви с емкостью
 . (6.40)
. (6.40)
Ток, протекающий в ветви с активным сопротивлением
 . (6.41)
. (6.41)
Ток в неразветвленной части цепи согласно первому закону Кирхгофа
 (6.42)
(6.42)
так как
 , (6.43)
, (6.43)
то
 (6.44)
(6.44)
и, следовательно, ток в неразветвленной части цепи или скорость изменения заряда
 . (6.45)
. (6.45)
Установленная аналогия между упругими, вязкими и пластическими параметрами горных пород и соответствующими им элементами электрических цепей, а также идентичность процессов, протекающих в механических и электрических моделях, позволяет обобщить эти закономерности.
Метод электрогидродинамических аналогий (метод ЭГДА)
Метод ЭГДА успешно применяют для изучения стационарных физических процессов, которые описываются уравнениями эллиптического вида.
В этом случае метод ЭГДА применяется в горном деле и гидротехнике для решения задач фильтрации жидкости; в электротехнике – для решения задач электропередачи; в строительной механике – при решении задач теории упругости; в теплотехнике – для решения задач теплообмена, а также для решения задач диффузии газа и жидкости, распространения магнитных, электрических и взрывных волн и др.
В ряде случаев, используя метод суперпозиций, метод ЭГДА может быть применен и для решения нестационарных физических процессов, которые описываются уравнениями параболического типа, например, задачи замораживания горных пород и фильтрации жидкости и газа в пористых средах, физические процессы которых протекают весьма медленно во времени. В этом случае изучение процесса в заданный период времени разбивается на сравнительно короткие промежутки времени, в течение которого физический процесс может рассматриваться как стационарный с соответствующим заданием граничных условий.
Метод ЭГДА основан на математической аналогии между некоторыми физическими процессами: например, между стационарным движением электрического тока в проводящей среде или стационарным распространением тепла в твердых телах, диффузией газа и жидкости и т.д.
Рассмотрим аналогию указанных выше процессов на примере аналогии
между стационарным движением электрического тока в проводящей среде и стационарным движением жидкости в пористых средах. Для упрощения процесса рассмотрим для плоскости (двухмерная задача). В этом случае процессы описываются следующими уравнениями
 ; (6.55)
; (6.55)
уравнение неразрывности
 . (6.56)
. (6.56)
Для фильтрующих пород:
уравнение движения
 (6.57)
(6.57)
уравнение неразрывности
 (6.58)
(6.58)
где  – электрический потенциал;
– электрический потенциал;
 – электропроводность материала;
– электропроводность материала;
 – пьезометрический напор;
– пьезометрический напор;
 – коэффициент фильтрации;
– коэффициент фильтрации;
 – компоненты плотности тока;
– компоненты плотности тока;
 – компоненты скорости потока;
– компоненты скорости потока;
 – координаты поверхности.
– координаты поверхности.
Если среды однородные, то коэффициенты электропроводности и фильтрации будут постоянными. В этом случае вместо уравнений (6.55), (6.57) получим уравнения Лапласа:


Исходя из этих уравнений, устанавливают аналогию между процессами и отдельными параметрами (табл.6.2).
Таблица 6.2
| Электрическое поле тока | Поле фильтрации жидкости | Магнитное поле | Поле температур |
Закон Ома:  ; ;  , где , где  – плотность тока; – плотность тока;  – электропроводность; – электропроводность;  – электрический потенциал; – электрический потенциал; 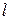 – сила тока. – сила тока. | Закон Дарси:  ; ;  , где , где  – скорость фильтрации; – скорость фильтрации;  – коэффициент фильтрации; – коэффициент фильтрации;  – пьезометрический напор; – пьезометрический напор;  – фильтрационный расход. – фильтрационный расход. | Закон магнитной индукции:   где где  – магнитная индукция; – магнитная индукция; 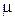 –магнитная проницаемость; –магнитная проницаемость;  – магнитный потенциал; – магнитный потенциал;  – магнитный поток. – магнитный поток. | Закон Фурье:   , где , где 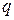 – тепловой поток; – тепловой поток;  – коэффициент теплопроводности; – коэффициент теплопроводности;  – температура; – температура;  – тепловой поток. – тепловой поток. |
Таким образом, исследование вопросов фильтрации в натуре сводят к изучению соответствующих (аналогичных) электрических процессов и параметров на электрических моделях, и результаты этих исследований распространяют на процессы фильтрации.
При осушении месторождений полезных ископаемых в результате работы водопонизительных скважин образуется депрессионная поверхность, на основании которой ведутся все гидрогеологические расчеты (дебит скважин и установки в целом, расположение скважин в плане, приток воды в горные выработки, закладка фильтров и т.д.). Для получения на электрической модели процессов аналогичных процессам фильтрации жидкости в натуре, необходимо выполнить ряд условий, вытекающих из общей теории подобия.
1. Электрическая модель должна представлять изучаемую область фильтрации жидкости в натуре в некотором масштабе без всякого искажения, т.е. должно быть соблюдено геометрическое подобие.
2. Коэффициент электропроводности модели должен быть прямо пропорционален в сходственных точках коэффициенту фильтрации жидкости, т.е. между моделью и натурой должно быть соблюдено физическое подобие
 . (6.59)
. (6.59)
3. Также должны быть подобны граничные условия модели и натуры, т.е. должно быть соблюдено динамическое подобие
 . (6.60)
. (6.60)
Подставив значения параметров фильтрации из выражений (6.59) и (6.60) в выражение (6.57), после преобразований получают
 (6.61)
(6.61)
Следовательно, уравнения (6.55) и (6.61) будут аналогичными в том случае, если произведение коэффициентов в квадратных скобках будет постоянно:
 . (6.62)
. (6.62)
Для однородной среды при  и
и  условия физического подобия выполняются автоматически, т.е. имеет место автомодельность. Поэтому при моделировании физических процессов необходимо соблюдать только геометрическое и динамическое подобие.
условия физического подобия выполняются автоматически, т.е. имеет место автомодельность. Поэтому при моделировании физических процессов необходимо соблюдать только геометрическое и динамическое подобие.
Исследование процесса осушения водоносных пород в конечном счете сводится к определению напоров воды на различных участках изучаемого пространства. Следовательно, на электрической модели необходимо построить поле потенциала, которое было бы аналогичным депрессионной поверхности воды в натуре. Пересчет электрического потенциала на напоры воды производится на основании граничных условий моделирования, которые могут быть записаны следующим образом:
 , (6.63)
, (6.63)
где  и
и  – постоянные коэффициенты.
– постоянные коэффициенты.
При этом:
при  должно быть
должно быть  ;
;
при  должно быть
должно быть  .
.
В этом случае будем иметь:
 (6.64)
(6.64)
 . (6.65)
. (6.65)
Значения максимальных и минимальных напоров воды обычно известны. Максимальный напор воды  имеет место на границе области питания и определяется гидрогеологическими разведочными скважинами. Контур питания определяется гидрогеологическими расчетами или непосредственными наблюдениями в скважинах при опытных откачках. Минимальный напор воды
имеет место на границе области питания и определяется гидрогеологическими разведочными скважинами. Контур питания определяется гидрогеологическими расчетами или непосредственными наблюдениями в скважинах при опытных откачках. Минимальный напор воды  задают из условий работы водопонизительных скважин. На электрической модели в соответствии с заданием максимального и минимального напоров воды задают максимальные и минимальные напряжения
задают из условий работы водопонизительных скважин. На электрической модели в соответствии с заданием максимального и минимального напоров воды задают максимальные и минимальные напряжения  и
и  . Обычно на модели эквипотенциальные поля строятся в относительных величинах. При этом
. Обычно на модели эквипотенциальные поля строятся в относительных величинах. При этом  берется за 1, а
берется за 1, а  0. Подставив значения
0. Подставив значения  = 1 и
= 1 и  = 0 в выражения (6.64) и (6.65), получим:
= 0 в выражения (6.64) и (6.65), получим:
 (6.66)
(6.66)
Следовательно, значение потенциала в любой точке поля будет определяться формулой
 . (6.67)
. (6.67)
Зная значения  и
и  и значение потенциала
и значение потенциала  на модели (определяется прибором), получим для напорной фильтрации значение напора
на модели (определяется прибором), получим для напорной фильтрации значение напора  в любой точке изучаемой области натуры:
в любой точке изучаемой области натуры:
 . (6.68)
. (6.68)
В случае безнапорной фильтрации пересчет от потенциалов к напорам производится по формуле
 . (6.69)
. (6.69)
При напорно-безнапорной фильтрации каждая из вышеприведенных формул (6.68) и (6.69) применяется в соответствующей области. Граница между ними определяется из условия
 , (6.70)
, (6.70)
где  – мощность водоносного пласта.
– мощность водоносного пласта.
Принцип действия установки ЭГДА основан на использовании для производства экспериментов мостового (компенсационного) метода измерений электрического потенциала в поле модели. Принципиальная электрическая схема установки ЭГДА (рис.6.4) состоит из блока питания и блока измерения.
 В блок питания входят: понизительный трансформатор 1, выпрямитель 2 и измерительные приборы – вольтметр 3 и миллиамперметр 4. В блок измерений входит: градуированный потенциометр 5, нуль-индикатор (гальванометр) 6 и поисковая игла 7.
В блок питания входят: понизительный трансформатор 1, выпрямитель 2 и измерительные приборы – вольтметр 3 и миллиамперметр 4. В блок измерений входит: градуированный потенциометр 5, нуль-индикатор (гальванометр) 6 и поисковая игла 7.
Если поисковой иглой подключиться к модели в какой-то точке  , то будут иметь место отмеченные на схеме токи
, то будут иметь место отмеченные на схеме токи  и потенциал
и потенциал  . Если же градуированное сопротивление потенциометра 5 отрегулировать так, чтобы потенциал
. Если же градуированное сопротивление потенциометра 5 отрегулировать так, чтобы потенциал  в точке
в точке  был равен потенциалу
был равен потенциалу  в точке
в точке 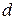 , то мост будет уравновешен, в чем убеждаются по отсутствию отклонения стрелки гальванометра: так как
, то мост будет уравновешен, в чем убеждаются по отсутствию отклонения стрелки гальванометра: так как  , то
, то  .
.
При уравновешенном мосте в силу разности потенциалов в точках а и б ток пойдет частично через модель, а частично через градуированный потенциометр и тогда:



 .
.
Если  , то
, то 
 .
.
Разделив их, получим
 , (6.71)
, (6.71)
а так как  (в сети гальванометра), то
(в сети гальванометра), то  и
и  .
.
Отсюда получаем уравнение равновесия моста
 или
или  (6.72)
(6.72)
Принимая сопротивление модели за усредненно-линейное, получаем значение потенциала  на всей линии
на всей линии  . Это и есть линия равного потенциала
. Это и есть линия равного потенциала  . Но так как
. Но так как  , то по шкале градуированного потенциометра в момент равновесия мостовой схемы получим значение потенциала
, то по шкале градуированного потенциометра в момент равновесия мостовой схемы получим значение потенциала  в той точке, где установлена поисковая игла.
в той точке, где установлена поисковая игла.
Из теории моста следует, что
 . (6.73)
. (6.73)
Отсюда ясно, что результаты измерений потенциалов на моделях не зависят от величины напряжения, приложенного на шинах модели, т.е. при изменении напряжения  (при колебании напряжения в питательной сети) одновременно и пропорционально изменяется падение напряжения
(при колебании напряжения в питательной сети) одновременно и пропорционально изменяется падение напряжения  . Поэтому разность потенциалов
. Поэтому разность потенциалов  может быть условно принята равной единице, а различные эквипотенциальные линии на модели будут лежать в пределах от нуля до единицы.
может быть условно принята равной единице, а различные эквипотенциальные линии на модели будут лежать в пределах от нуля до единицы.
Зная значения отдельных эквипотенциалей [или в пересчете по формулам (352), (353) напоров] и кратчайшие расстояния между ними, можно определить величину градиентов, а также плотность тока или скорости фильтрации.
Таким образом, метод ЭГДА дает возможность заменить исследования фильтрационного потока в натуре исследованием электрического поля на модели и результаты исследования перенести в натуру.
Моделирование тепловых процессов в горном деле
Дифференциальное уравнение теплопроводности в случае постоянных физических параметров тела имеет следующий вид:
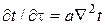 . (4.68)
. (4.68)
где  – температура тела, отсчитанная от температуры среды, окружающей
– температура тела, отсчитанная от температуры среды, окружающей
твердое тело, как от нуля;
 – время;
– время;
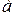 –коэффициент температуропроводности, постоянный во всем теле;
–коэффициент температуропроводности, постоянный во всем теле;
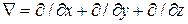 – оператор Лапласа;
– оператор Лапласа;
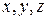 – координаты.
– координаты.
Приведенное уравнение (4.68) описывает бесконечное множество рассматриваемых тепловых процессов. Чтобы из целого класса явлений выделить единичное явление, необходимо к этому уравнению присоединить начальные и граничные условия, а также задать значение коэффициента температуропроводности 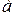 .
.
Начальное условие должно представлять собой распределение температур во всей исследуемой области для момента времени 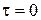 и может быть записано в виде
и может быть записано в виде
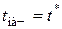 , (4.69)
, (4.69)
где 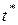 – известная температура в фиксированной точке тела с координатами
– известная температура в фиксированной точке тела с координатами
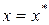 ,
, 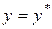 ,
, 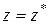 в начальный момент времени.
в начальный момент времени.
Граничные условия могут быть заданы в виде равенства тепловых потоков на поверхности тела.
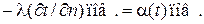 , (4.70)
, (4.70)
где  – коэффициент теплопроводности, постоянный во всем теле;
– коэффициент теплопроводности, постоянный во всем теле;
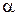 – коэффициент теплоотдачи;
– коэффициент теплоотдачи;
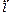 – внешняя нормаль к поверхности тела.
– внешняя нормаль к поверхности тела.
Коэффициент теплоотдачи 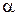 в общем случае зависит от координат поверхности и времени. Поэтому, выражение для коэффициента теплоотдачи может быть записано в следующем виде:
в общем случае зависит от координат поверхности и времени. Поэтому, выражение для коэффициента теплоотдачи может быть записано в следующем виде:
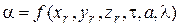 , (4.71)
, (4.71)
где 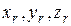 – координаты границы (поверхности) твердого тела.
– координаты границы (поверхности) твердого тела.
Для установления подобия процессов в рассматриваемом случае необходимо дифференциальные уравнения, начальные и краевые условия привести к безразмерному виду и обеспечить равенство безразмер
