Напряжения в ремне и их круговая эпюра

1) напряжение от окружного усилия:

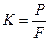
Для плоских ремней площадь сечения ремня

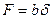
где b - ширина, d - толщина ремня.

Для клиновых ремней F определяется по таблицам ГОСТа.

2) напряжение от предварительного натяжения ремня:

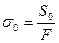
3) напряжение от усилий натяжения ремня:

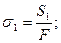
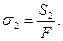
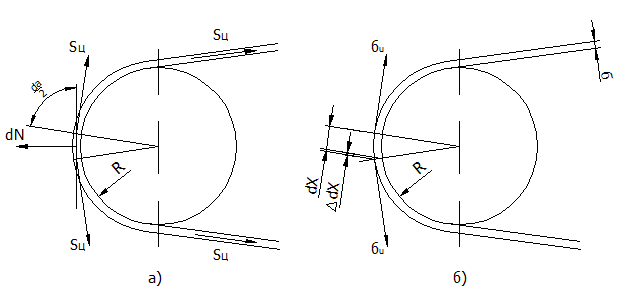
Рис. 56

4) напряжение от действия центробежных сил: Рассматривая сумму проекций сил на горизонтальную ось (рис.56 а), получим:

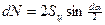
Синус элементарного угла 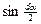можно принять равным углу в радианах 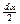; тогда центробежная сила элементарного участка ремня, введенного дугой :

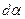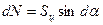(1)

с другой стороны, элементарная центробежная сила:

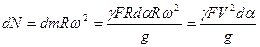(2)

Здесь: dm - элементарная масса выделенного участка ремня;

R - радиус шкива;

w - угловая скорость вращения шкива;

g - удельный вес материала ремня;

V - окружная скорость ремня;

g - ускорение силы тяжести.

Приравнивая уравнение (1) и (2) и уравнивая размер­ности, получим натяжение ремня от действия центробежной силы:

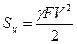
Напряжение в ремне от действия центробежной силы:

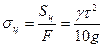
Следует заметить, что напряжение пропорционально квадрату окружной скорости; при малых скоростях оно неве­лико, при больших - резко возрастает.

5) напряжение от изгиба ремня:

Рассматривая подобие фигур (рис. 56 б), можно написать:

;

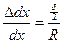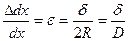
По закону Гука 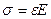; 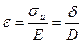, отсюда

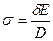
Напряжение изгиба пропорционально толщине ремня, мо­дулю упругости и обратно пропорционально диаметру шкива. Это значит, что отношение 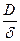не должно быть малым (оно указывается в таблицах ГОСТа для каждого типа ремня).

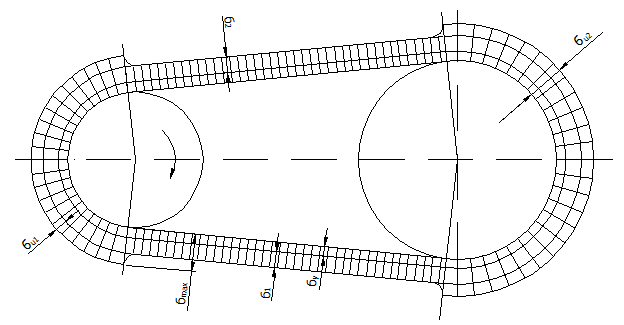
Рис. 57

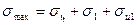
Расчет ременных передач до тяговой способности

а) плоские ремни:

;

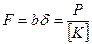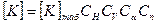
Здесь: [К] - допускаемое расчетное напряжение;

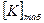- табличное допускаемое напряжение;

C_H - поправочный коэффициент, зависящий от ха­рактера нагрузки;

C_V - поправочный коэффициент, зависящий от скорости ремня;

C_a - поправочный коэффициент, зависящий от угла обхвата ремня;

C_n - поправочный коэффициент, зависящий от расположения передачи.

При горизонтальном расположении С_n = 1.

Расчет имеет условный характер и базируется на выбо­ре допускаемых напряжений по кривым скольжения, которые уточняются табличными поправочными коэффициентами.

б) клиновые ремни:

Число ремней:

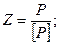
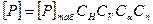
Здесь: [Р] - допускаемая расчетная нагрузка на ремень;

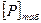- табличная допускаемая нагрузка.

Глава IX

ФРИКЦИОННЫЕ ПЕРЕДАЧИ

Главным достоинством фрикционных передач, а которых окружное усилие передается за счет сил трения между катками, является возможность создания на их базе фрикционных вариаторов (бесступенчатых коробок передач). К достоинст­вам можно отнести также то, что эти передачи работают бес­шумно даже на сверхвысоких скоростях и сравнительно просты по конструкции.

Главный недостаток – ограниченная передаваемая мощ­ность в связи с отсутствием пока достаточно прочных материалов.

Для того чтобы передать заданное окружное усилие Р, фрикционные катки надо при-жать друг к другу усилием Q так, чтобы возникающая при этом сила трения F была бы больше силы Р на величину коэффициента запаса сцепления b, который принимают равным b = 1, 25 + 2, 0.

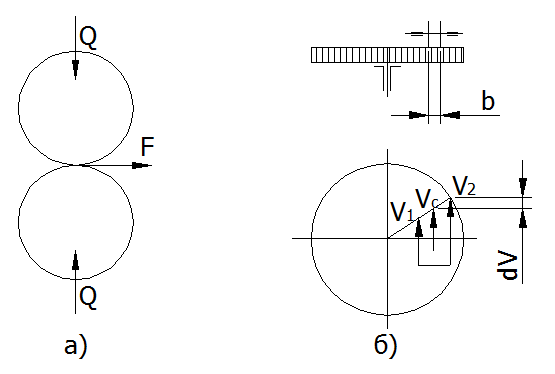
Рис. 58

Значения коэффициента трения между катками в среднем:

сталь или чугун по коже или ферродо насухо f = 0,3;

то же в масле f = 0,1;

сталь или чугун по стали или чугуну насухо f = 0,15;

то же в масле f = 0,07.

Подставив эти значения в уравнение, можно убедиться в том, что усилие прижатия фрикционных катков во много раз превышает передаваемое окружное усилие.

Геометрическое скольжение

Помимо упругого скольжения катков, которое возникает так же, как и в ременных передачах, во фрикционных передачах может иметь место еще геометрическое скольжение вслед­ствие разности скоростей ведущего и ведомого катков по длине контакта b (рис.58 6).

Геометрическое скольжение не позволяет катки делать широкими, вследствие чего в передаче возникают большие контактные напряжения, ограничивающие передаваемую мощ­ность.

Вариаторы

Вариаторы разделяются на два основных типа:

а) простые, в которых изменяется только один радиус контакта, а другой остается постоянным;

б) сложные, в которых изменяются оба радиуса.

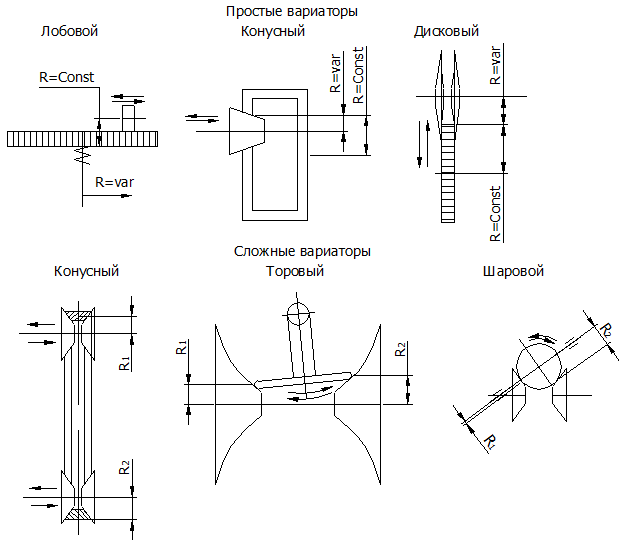
Рис. 59

В простых вариаторах передаточное отношение:

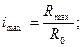
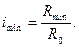
Диапазон регулирования:

.

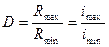В сложных вариаторах передаточное отношение:

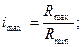
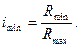
Диапазон регулирования:

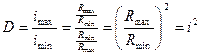
В сложных вариаторах передаточное отношение может принимать значения, равные:

I > 1; I <1; I = 1.

Диапазон регулирования равен квадрату максимального передаточного отношения. Это значительно расширяет область применения сложных вариаторов.