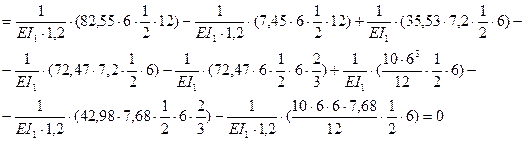Определяем число степеней свободы.
D=1, У=0, Ш=0, С=0, Соп=6.
W= 3D+2Y-2Ш-С- Соп =3+0-0-0-6=-3
Система может быть статически неопределимой и геометрически неизменяемой.
1.3 Выполняем анализ геометрической структуры.
Диск D1 крепится к диску “Земля” шестью опорными стержнями, которые не параллельны друг другу и не пересекаются в одной точке образуя с ней единый диск
1.4 Система геометрически неизменяемая и статически неопределимая с избыточным числом связей.
1.5 Определяем степень полной внутренней и внешней статической неопределимости.
Л= 3К-Ш=3·2-1=5;
Л1= Соп -3- Сзам = 6-3-0 = 3;
Л2=Л-Л1 =5-3 =2.
Основная система. Кинематические уравнения метода сил.
2.1 Изображаем возможный вариант основной системы.

Выделим симметричную и антисимметричную составляющие внешней нагрузки.
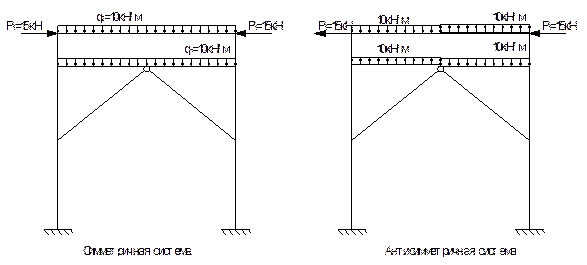
Выделим симметричные и антисимметричные составляющие основных неизвестных в основной системе.
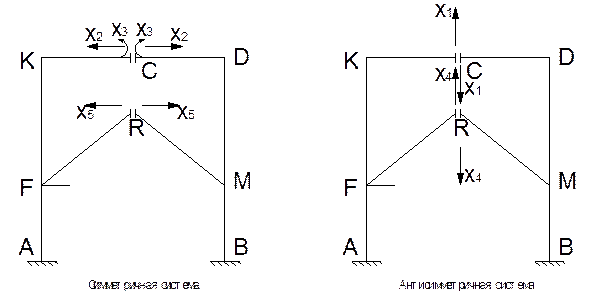
Составим систему кинематических уравнений отдельно для симметричной и антисимметричной составляющий нагрузки.
Симметричная система
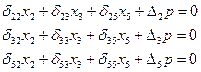
Антисимметричная система
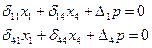
3.Единичные состояния основной системы при действии симметричной и антисимметричной составляющий нагрузки. Определение коэффициентов dik.
3.1 Рассмотрим единичные состояния в антисимметричной системе от действия 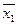 и
и 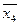 .
.
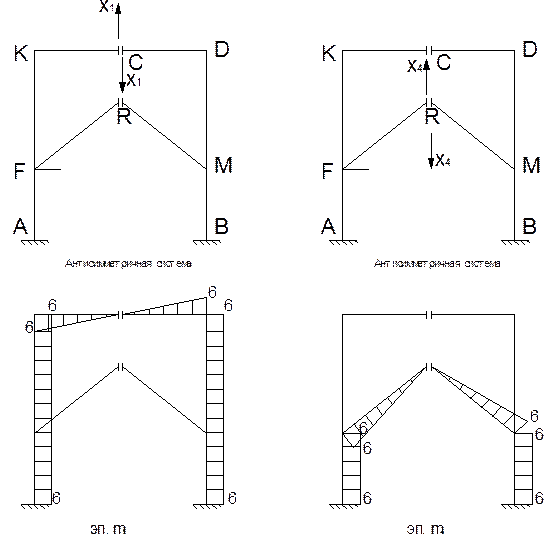
FR=RM= 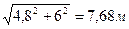 ;
;
sina= 4,8/7,68=0,625;
соsa= 6/7,68=0,781;
tga= 4,8/6=0,8;
ctga=6/4,8=1,25.
3.2 Определяем величину коэффициентов dik по формуле.
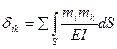 ;
;
d14 = 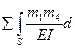 S =
S = 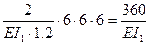 ;
;
d44 = 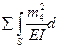 S =
S = 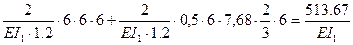 ;
;
d11 = 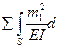 S =
S = 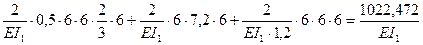 .
.
3.3 Выполним кинематическую проверку правильности определения коэффициента dik.
Для этого построим суммарную эпюру равную Sms=m1+m4, а затем эпюру ms перемножим саму на себя по правилу Верещагина.
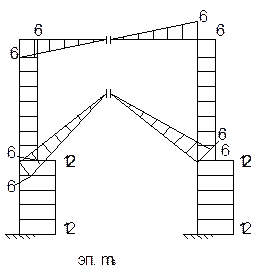
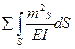 =
=
= 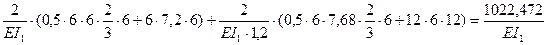
Коэффициенты dik найдены верно.
3.4 Грузовое состояние основной системы. Определение свободных членов Diр. Рассмотрим основную систему в грузовом состоянии и построим эпюру МР.
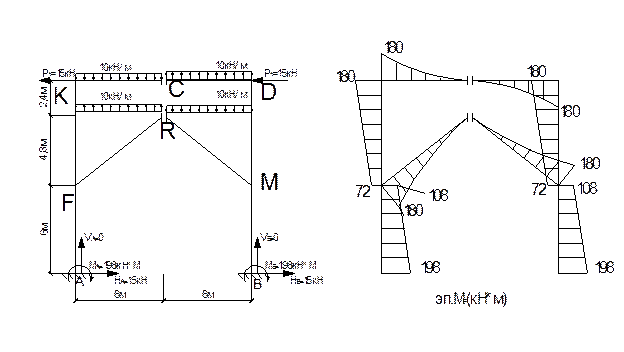 Определяем опорные реакции.
Определяем опорные реакции.
SМ А=0;
МА+q1·6·3 –q2·6·3 -Р1×13,2=0;
МА=180-180+198=198кН·м;
SМ c=0;
-МА+q2·6·3 -q1·6·3 -VА·6+НА·13,2=0;
Sх=0;
НА-Р1=0, НА=15кН;
VА =-198+180-180+198/6=0;
SМ В=0;
-МВ+q1·6·3 –q2·6·3 +Р1×13,2=0;
МВ=180-180+198=198кН·м;
SМ c=0;
-МВ+q2·6·3 -q1·6·3 –VВ·6+НВ·13,2=0;
Sх=0;
НВ-Р1=0, НВ=15кН;
VВ =-198+180-180+198/6=0;
Участок СD.
0 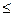 х
х 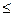 6м.
6м.
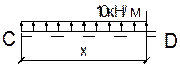
М=q2(х2/2);
при х=0 М=0;
при х=6м М=10·(36/2)=180кН·м;
Участок DM.
0 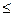 х
х 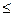 7,2м.
7,2м.
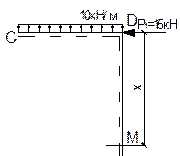
М=q2(62/2)- Р1×х;
при х=0 М=180кН·м;
при х=7,2м М=10·(36/2)-15·7,2=72кН·м;
Участок МВ.
0 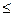 х
х 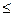 6м.
6м.
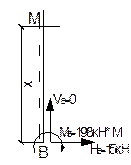
М=НВ·х- МВ;
при х=0 М= МВ =-198кН·м;
при х=6м М=15·6-198=-108кН·м;
Участок RМ.
0  х
х  4,8м.
4,8м.
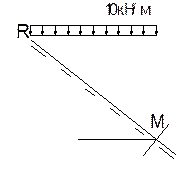
М=-q1(х·сtga2/2);
при х=0 М= 0;
при х=4,8м М=-10·((4,8·1,25)2/2) =-180кН·м;
Участок СK.
0  х
х  6м.
6м.
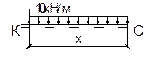
М=-q2(х2/2);
при х=0 М=0;
при х=6м М=-10·(36/2)=-180кН·м;
Участок KF.
0  х
х 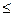 7,2м.
7,2м.
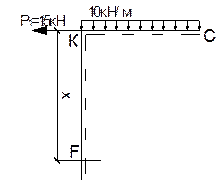
М=-q2(62/2)+ Р1×х;
при х=0 М=-180кН·м;
при х=7,2м М=-10·(36/2)+15·7,2=-72кН·м;
Участок FA.
0 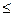 х
х 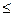 6м.
6м.
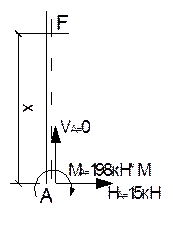
М=-НA·х+ МA;
при х=0 М= МA =198кН·м;
при х=6м М=-15·6+198=108кН·м;
Участок FR.
0  х
х  4,8м.
4,8м.
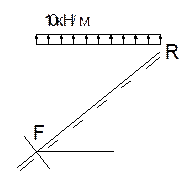
М=q1(х·сtga2/2);
при х=0 М= 0;
при х=4,8м М=10·((4,8·1,25)2/2) =180кН·м;
3.5 Определяем величину свободных членов Diр по формуле Максвелла-Мора.
Dip= 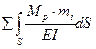 ;
;
D1p= 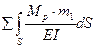 =
=
= 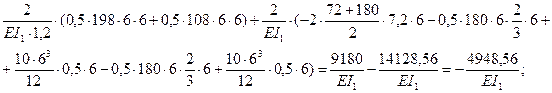
D4p= 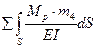 =
=
= 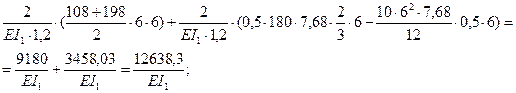
3.6 Выполним кинематическую проверку правильности определения свободных членов.
Для этого эпюру МР перемножим по правилу Верещагинана суммарную единичную эпюру mS. В результате мы должны будем получить сумму свободных членов системы канонических уравнений метода сил.
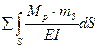 =
=
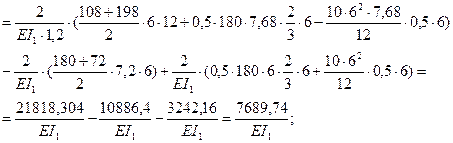
SDip =D1p +D4p= 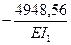 +
+ 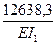 =
= 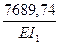 ;
;
Коэффициенты Dip найдены верно.
Составляем систему.
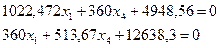
Решая систему находим х1=17,9214, х4=-37,1642.
3.8 Строим эпюры m1х1 и m4х4.
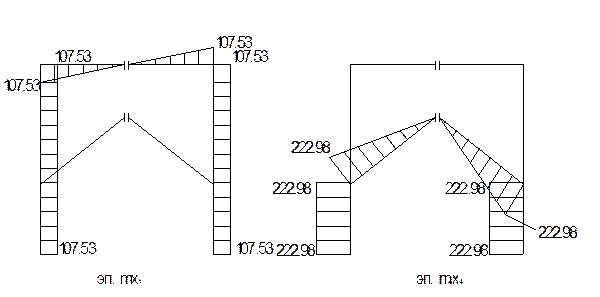
3.9 Строим окончательную эпюру М= Мр+m1х1+m4х4.
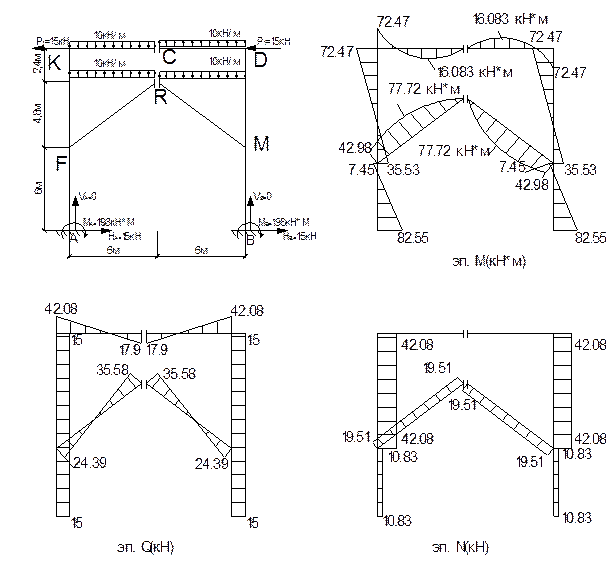
Выполним кинематическую проверку .
Для этого эпюру М перемножим по правилу Верещагинана суммарную единичную эпюру mS.
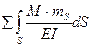 =
=