Математическое словоупотребление

Возьмём мешок:

Верно ли утверждение «Все бусины в этом мешке — квадратные»? Вероятно, вы скажете, что верно. Однако многие люди, в том числе и ваши ученики, могут сказать: «Как же так, в утверждении говорится все, а здесь всего одна бусина! Данное утверждение или бессмысленно, или неверно». На это можно возразить, приведя такой пример. Вы просите всех, кто не сделал домашнее задание, поднять руки и обещаете всем, кто его не сделал, поставить двойку (и всем, кто поднял руку, дать возможность эту двойку исправить). Поднял руку один Вася (все остальные домашнее задание сделали). Верно ли, что подняли руку все, кто задание не сделал? Кажется, да. Если вы поставите бездельнику Васе двойку, верно ли, что все, кто не сделал домашнего задания, получили двойку? Скорее всего верно. Но ведь Вася один! Этот пример может кого-то убедить.

Дело, однако, не в убедительности примера, а в том, что некоторые слова математики используют не «по здравому смыслу» (хотя и согласуясь с ним), а «по договорённости». Это значит, что они, заранее договорившись о смысле какого-то слова, дальше всегда используют именно его, несмотря на то что слово может иметь и другие смыслы в обычном языке. Важно при этом, что математики заботятся о том, чтобы такие договорённости были осмысленными и простыми.

Например, математики договорились и о том, как понимать смысл слова существует. Когда они говорят, что в мешке существует, найдётся объект с данными свойствами, то это верно, если в мешке объект с этим свойством один или больше или даже все объекты в мешке обладают этим свойством.

Задача 36. Здесь дети впервые сталкиваются с явным употреблением понятия «все» в случае, когда объект всего один. Например, третий пункт инструкции гласит: «Раскрась все квадратные бусины четвёртого уровня синим», а среди бусин четвёртого уровня квадратная бусина всего одна.

Задача 37. В отличие от задачи 36, где нужно было найти на готовом дереве бусины на разных уровнях, в этой задаче даны мешки бусин первых трёх уровней дерева, детям необходимо нарисовать дерево в окне. Здесь, как и во всех подобных задачах, окно в рабочей тетради разделено на уровни. Мы надеемся, что это поможет детям правильно расположить бусины дерева по уровням и нарисовать в окне аккуратное дерево. Учащийся может, например, сразу нарисовать бусины из каждого мешка на соответствующем уровне (конечно, в любом порядке), добавить по желанию бусины на четвёртом и пятом уровнях, а потом уже соединить все нарисованные бусины в дерево.

Задача 38 (необязательная).Задача на повторение понятий «все», «есть», «нет». Как и в других задачах со словом все, здесь необходим полный перебор всех месяцев года и проверка для каждого из них обоих условий. Условию задачи удовлетворяют три слова.

Задача 39. В задаче настолько мало ограничений, что кто-то, прочитав условие, возможно, будет просто сидеть, не зная с чего начать. На самом деле можно нарисовать первое дерево каким угодно, а затем из его бусин сконструировать второе дерево так, чтобы уровней в нём было больше (или меньше).

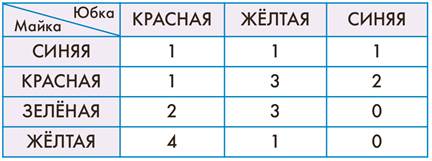
Задача 40. Одинаковое общее количество мышей в таблице и в мешке является необходимым, но не достаточным условием правильности решения. Если эти числа не совпадают, то в решении точно допущена ошибка, если же они совпадают, то это не гарантирует правильности заполнения таблицы. Ребёнок мог, заполняя одну клетку, сосчитать какую-то мышь дважды, а заполняя другую клетку, пропустить одну мышь.

Таблица будет заполнена верно, если не только общее число мышей, но и суммы по строкам и столбцам будут совпадать с действительным числом мышей в мешке, обладающих именно этим одним признаком. В мешке 6 мышей в красных майках, значит, сумма всех клеток верхней строки должна быть равна шести. Если это условие не выполняется для какой-то строки или столбца, то так мы узнаём, каких мышек нужно снова пересчитать. Этот метод можно использовать и в случае, если у ребёнка сразу не сошлось число мышей в таблице и в мешке. Чтобы не пересчитывать всё заново, можно посчитать число мышей в майках каждого цвета, а затем проверить суммы по строкам. В строке, где эти числа не сойдутся, нужно искать ошибку. Если провести такую работу ещё и по столбцам, то можно будет назвать клетку таблицы, где число вписано неверно.

Решение задачи:

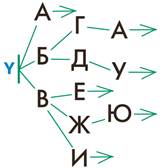
Задача 41. Начинать решать задачу можно так же, как и задачу 37: написать сначала все буквы на своих уровнях. Здесь уже нельзя соединять буквы в дереве как угодно: нужно, чтобы были истинны оба утверждения. Из первого утверждения следует, что после каждой гласной на каждом уровне можно сразу поставить стрелочку листа. Рисуем стрелочки, читаем второе утверждение. Если все листья — это гласные, то других листьев, кроме уже помеченных на дереве, быть не должно. Остаётся соединить буквы, учитывая, что все согласные буквы не являются листьями и обязательно должны иметь хотя бы одну следующую букву. Эта задача не требует общего обсуждения. Проходя по классу, вам будет достаточно указать ученику на то, что для какой-либо буквы полученного им дерева одно из утверждений ложно, — дальше он скорее всего справится сам.

Обратите внимание, все ли дети справились с ситуацией, связанной с мнимой похожестью утверждений, данных в задаче. Возможно, кто-то спросит, зачем здесь два утверждения, в которых говорится «одно и то же». По опыту учителей математики среднего звена известно, что часто детям и в 7 классе, например, утверждения «Вертикальные углы равны» и «Равные углы вертикальны» кажутся одинаковыми. Поэтому, если у кого-то такой вопрос возник, советуем остановиться и на понятных примерах показать, что первое и второе утверждения различаются по содержанию. Советуем привести понятные примеры, например, утверждения «Все мальчики нашего класса — отличные спортсмены» и «Все отличные спортсмены — мальчики нашего класса» означают не одно и то же (первое может быть истинным, а второе явно ложное). Если на примерах из жизни все понятно, то можно вернуться к задаче и попробовать построить дерево.

Ответ: вариантов правильных ответов к этой задаче довольно много. Мы приводим только один из них.

Задача 42. Помимо повторения темы «Словарный порядок», в задаче проводится пропедевтика видов сортировки, в частности упорядочения. На примере этой задачи ребята могут увидеть, что упорядочить одни и те же элементы можно по разным критериям. Одним из таких критериев расстановки слов является словарный порядок, другим — календарный порядок месяцев. Конечно, можно придумать и другие принципы упорядочения. Например, по возрастанию (убыванию) числа букв в названии месяца, а если число букв двух месяцев одинаково — по алфавиту. Можно упорядочивать в обратном словарном порядке и т. д.

Задача 43 (необязательная).Важно обсудить с детьми, как они решали задачу. Как обычно, стратегии здесь могут быть разными: систематически перебирать все пары, перебирать пары наугад (метод проб и ошибок). При поиске одинаковых мешков также полезно использовать разные особенности конкретного набора мешков: некоторые объекты есть почти в каждом мешке, другие — только в небольшом числе мешков. Начав рассматривать ситуацию под этим углом зрения, мы обнаруживаем, что, например, лампочка есть в каждом мешке. Открыв эту закономерность, мы можем «перестать видеть» лампочки в мешках, не сравнивать мешки по наличию в них лампочек и т. д.

Ещё одна хорошая идея — пересчитать число объектов в каждом мешке и разбить их на группы по этому числу. Такая идея уже использовалась ранее, и не исключено, что кто-то из детей её вспомнит или изобретёт заново. Оказывается, что во всех мешках по четыре предмета.

Ещё одна из идей может состоять в том, чтобы перейти от наглядного, но из-за различного взаимного расположения предметов сбивающего с толку представления к более формальному. В частности, перейти от мешка к его таблице. Такую таблицу удобно выписывать сокращённо, просто в виде списка, столбиком (например, рядом с мешком), указывая в алфавитном порядке, какие объекты в мешке есть: (В)илка, (К)арандаш, (ЛА)мпочка, (ЛО)жка, (Н)ож, (Ч)ашка. При этом, если мы уже исключили из рассмотрения электрическую лампочку и ложку, столбики будут иметь высоту 2. Потом надо будет искать одинаковые столбики.

При выполнении этой задачи необходимо дать как можно больше свободы для принятия решений каждому учащемуся. Индивидуальное обсуждение способа работы с задачей полезно только после того, как ребёнок уже нашёл решение или по крайней мере достаточно много потрудился над задачей и попросил вашей помощи. Эта задача является одной из подготовительных для проекта «Одинаковые мешки». В работе над проектом будет проведено общее обсуждение того, какие существуют способы решения подобных задач.

Задача 44 (необязательная).Эту задачу, как и многие другие задачи, можно решать методом перебора (последовательного или случайного) или уменьшить объём работы с помощью рассуждений или поиска некоторой закономерности. В данном случае нетрудно заметить, что некоторые буквы есть во всех словах (например, А или П), а некоторые — не во всех (например, У или Е). Так, слов с буквой У всего два, поэтому их можно сразу вычеркнуть. Среди оставшихся слов три слова с буквой Е и четыре слова — без неё. В одной из этих групп и находятся три искомых слова.

Задача 45 (необязательная).Не все окна здесь заполняются однозначно, да и сами мешки, которые получатся, возможно, будут разными.

Однозначно заполняются окна в четырёх словах:

... ... К ... НИБУДЬ КАК-НИБУДЬ

... ... К ... ... ... ... НИБУДЬ ОТКУДА-НИБУДЬ

... ... ... Е ... -НИБУДЬ ЗАЧЕМ-НИБУДЬ

... ... Е-НИБУДЬ ГДЕ-НИБУДЬ

Остальные слова делятся на группы в соответствии с количеством букв, идущих перед НИБУДЬ.

Три буквы (КЕМ-, КТО-, ЧЕЙ-, ЧЕМ-, ЧТО-):

К ... ... -НИБУДЬ КЕМ-/КТО-НИБУДЬ

... Е ... -НИБУДЬ КЕМ-/ЧЕЙ-/ЧЕМ-НИБУДЬ

Ч ... ... ... НИБУДЬ ЧЕЙ-/ЧЕМ-/ЧТО-НИБУДЬ

Четыре буквы (КОГО-, КОМУ-, КУДА-, ЧЕГО-, ЧЕМУ-):

... Е ... ... ... НИБУДЬ ЧЕГО-/ЧЕМУ-НИБУДЬ

ЧЕ ... ... ... НИБУДЬ ЧЕГО-/ЧЕМУ-НИБУДЬ

... ... М ... -НИБУДЬ КОМУ-/ЧЕМУ-НИБУДЬ

... О ... ... ... НИБУДЬ КОГО-/КОМУ-НИБУДЬ

Пять букв (КАКОЙ-, КОГДА-):

К ... ... ... ... ... НИБУДЬ КАКОЙ-/КОГДА-НИБУДЬ

К ... ... ... ... -НИБУДЬ КАКОЙ-/КОГДА-НИБУДЬ

Шесть букв (ОТЧЕГО-, ПОЧЕМУ-):

... ... ЧЕ ... ... ... НИБУДЬ ОТЧЕГО-/ПОЧЕМУ-НИБУДЬ

ОТ ... ... ... ... -НИБУДЬ ОТЧЕГО-НИБУДЬ

Когда мы всё выписали, шестибуквенные слова восстанавливаются однозначно, для двух пятибуквенных есть два варианта. Среди четырёхбуквенных слов КОМУ- и КОГО- восстанавливаются однозначно, а для пары ЧЕГО-/ЧЕМУ- есть два варианта. Вариантов заполнения трёхбуквенных слов есть довольно много.

Если кто-то запутался совсем, то попросите его найти в мешке слово, определяющееся однозначно, например КАК-НИБУДЬ или ОТКУДА-НИБУДЬ (первое и второе слова сверху). Глядя на то, как ученик работает, вы легко поймете, в чём причина ошибок. Скорее всего ребёнок забыл, что дефис — отдельный символ и должен занимать при заполнении окон отдельную бусину. Посоветуйте такому ученику сначала заполнить все окна, соответствующие дефисам (перед словом НИБУДЬ), а затем приступить к дальнейшей работе.

Проект «Одинаковые мешки»