Основы вариационного исчисления - II
Основы вариационного исчисления - II
Методические указания
и варианты заданий
для самостоятельной работы студентов
III курса специальностей КМ и ДПМ
Издательство
Пермского государственного технического университета
Составитель: В.В. Малыгина
УДК 517 (075.8)
О75
Рецензент:
канд. техн. наук, доцент кафедры ВММ И.Н. Бояршинова
Основы вариационного исчисления. Ч. II: метод. указания и варианты заданий для самостоятельной работы студентов III курса специальностей КМ и ДПМ / сост. В.В. Малыгина. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008. – 58 с.
Данное методическое пособие является продолжением пособия «Основы вариационного исчисления – I», сохраняя его обозначения и терминологию, а также продолжая нумерацию формул, примеров и заданий. В часть II вошли разделы «Вариационные задачи на плоскости и в пространстве», «Вариационные задачи с подвижными границами» и «Задачи на условный экстремум».
УДК 517 (075.8)
© ГОУ ВПО
«Пермский государственный
технический университет», 2008
Вариационные задачи с подвижными границами
В предыдущих лекциях при исследовании функционала
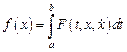
предполагалось, что граничные точки 
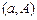и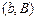 
заданы. Подобное предположение не всегда выполняется для многих интересных и практически важных вариационных задач. Рассмотрим в качестве примера задачу навигации.
Задача навигации
В этой задаче рассматривается река ширины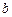 
с прямыми параллельными берегами. Считая один берег реки совпадающим с осью 
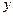, введем скорость течения реки 
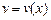. Лодка с постоянной скоростью
( 
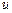– величина скорости, 
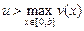), за кратчайшее время должна пересечь реку, отчалив из точки 
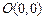(рис.1).
Обозначим через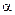 
угол, который образует вектор скорости лодки с положительным направлением оси 
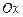. Тогда реальная скорость движения лодки в момент времени 
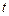определяется равенствами
, 
.
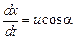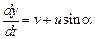Отсюда
,
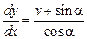что позволяет выразить 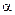через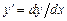 
:
,
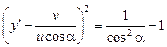откуда
.
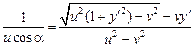Для времени пересечения реки находим
.
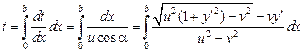Последний интеграл должен быть минимизирован за счет выбора функции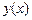 
при условии 
.
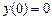Как видим, в отличие от предыдущих задач, правый конец искомой кривой заранее не определен: он может оказаться на любой точке вертикальной прямой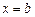 
. Мы приходим, таким образом, к задаче со свободной (подвижной) границей. Найдем ее решение в общей постановке.
Решение задачи навигации
Вернемся к задаче навигации и найдем ее решение, используя полученный выше результат.
Итак, нам следует найти минимум функционала
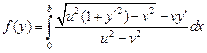
при условии 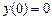, а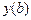 
может принимать любое значение.
Согласно вышеприведенной схеме, решаем уравнение Эйлера. Так как подынтегральная функция
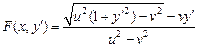
зависит только от 
и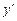 
, то уравнение Эйлера допускает первый интеграл: 
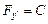. С другой стороны, поскольку вторая граница экстремали перемещается по вертикальной прямой, для нее должно выполняться условие 
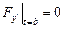. Отсюда сразу следует, что вышеприведенный первый интеграл имеет вид: 
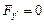. Получаем дифференциальное уравнение первого порядка
,
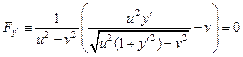для которого легко найти решение. Находя явное выражение для 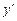, получаем 
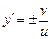. Так как предполагается (см. рис. 1), что переправа осуществляется с левого берега на правый, то перед дробью следует выбрать знак плюс. Учитывая, что 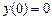, получаем окончательно:
.
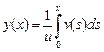В частности, если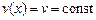 
, то искомый маршрут наибыстрейшей переправы реализуется на прямой 
.
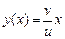Изопериметрическая задача
Интересный класс задач на условный экстремум образуют так называемые изопериметрические задачи. Классической задачей такого вида (давшей название всему классу задач) является задача Дидоны: найти замкнутую кривую, ограничивающую наибольшую площадь при заданном периметре. При этом и минимизируемый функционал (площадь) и ограничение (периметр) задаются определенными интегралами.
Рассмотрим задачу в общей постановке. Пусть на кривых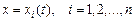 
с фиксированными концами 
, 
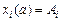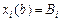функционал
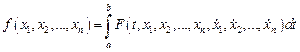
достигает своего минимального (максимального) значения, причем интегралы
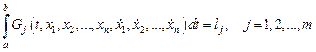
обладают заранее заданными значениями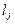 
. Функци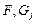и 
и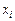 
считаются дважды непрерывно дифференцируемыми.
На первый взгляд кажется, что интегральные ограничения существенно усложняют задачу, и к изопериметрической задаче неприменимы методы предыдущего раздела. Однако оказалось, что изопериметрическую задачу остроумным приемом можно свести к задаче на условный экстремум с функциональными условиями связи.
Обозначим
.
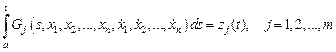Тогда
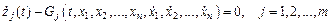
– новые условия связи, уже дифференциально-функционального вида, а изопериметрические условия превращаются в граничные условия:
.
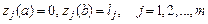Таким образом, задача свелась к задаче на условный экстремум, для которой выше был приведен алгоритм решения. Следуя ему, составляем вспомогательную функцию
,
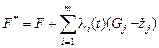для которой система уравнений Эйлера имеет вид:
.
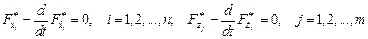Но так как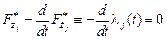 
, то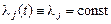 
, а тогда
.
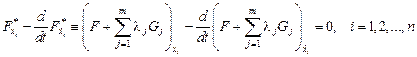Следовательно, для изопериметрической задачи в качестве функции Лагранжа можно взять функцию
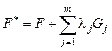
с постоянными множителями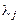 
. Далее для функции 
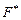, как и ранее, выписывается и решается система уравнений Эйлера, а для определения произвольных постоянных и параметров 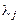используются граничные и изопериметрические условия. То обстоятельство, что множители 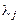оказываются постоянными, безусловно, упрощает решение задачи.
Пример 9.Найти экстремум функционала
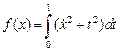
на классе функций, удовлетворяющих граничным условиям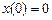 
, 
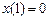и дополнительному условию 
.
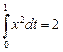Решение. Поставленная задача, очевидно, относится к классу изопериметрических задач, поэтому, согласно приведенной выше схеме, запишем вспомогательную функцию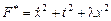 
, для которой составим уравнение Эйлера: 
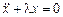. Так как знак 
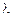неизвестен, решение уравнения Эйлера следует провести для каждого из трех случаев: 
, 
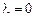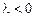и 
.
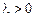- Пусть 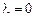, тогда решение уравнения Эйлера имеет вид
.
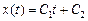Подставляя граничные условия, находим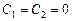 
, то есть 
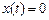. Но это решение не удовлетворяет условию 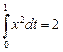, следовательно, при 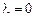решений у задачи нет.
- Пусть
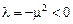, тогда решение уравнения Эйлера имеет вид
,
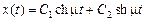из граничных условий снова получаем 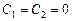, а 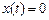, то есть при 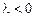задача также не имеет решений.
- Пусть
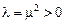, тогда решение уравнения Эйлера имеет вид
,
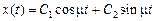подставляя граничные условия, находим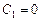 
, 
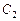– любое число, 
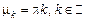. Следовательно, 
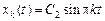, где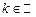 
. Определим 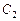через изопериметрическое условие:
.
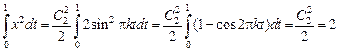Получаем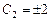 
, то есть 
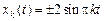. Так как 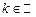, то можно оставить перед функцией один знак. Окончательно получаем, что данная вариационная задача имеет бесконечное множество решений вида:
.
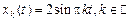Примеры решения некоторых вариационных задач
В качестве иллюстрации построенной теории решим три классические задачи: задачу Дидоны, задачу о брахистохроне и задачу о минимальной поверхности вращения. Каждую из этих задач сначала переформулируем в вариационных терминах, то есть поставим ее как задачу отыскания минимума функционала с заданными граничными условиями, а затем решим ее разработанными выше методами вариационного исчисления.
Задача Дидоны
Вспомним задачу, о которой говорилось в начале курса: мы оставили Дидону в тот момент, когда ей нужно было ограничить шнуром фиксированной длины максимальную площадь. Мы уже освоили вариационное исчисление настолько хорошо, что можем помочь Дидоне.
Рассмотрим множество функций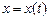 
, определенных на отрезке 
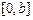, таких, что 
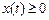при всех 
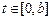, а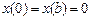 
(рис. 3). Вместе с отрезком 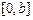график каждой функции 
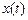ограничивает площадь, задаваемую функционалом
.
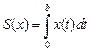Потребуем дополнительно, чтобы кривые 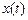имели фиксированную длину, то есть постоянное значение сохранял функционал вида:
.
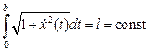Мы получаем, таким образом, изопериметрическую задачу, для которой нам уже известны методы решения.
Выстраиваем вспомогательную функцию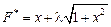 
и записываем для нее уравнение Эйлера. Функция 
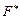не зависит от переменной 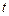, следовательно, уравнение Эйлера допускает первый интеграл
,
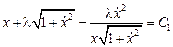представляющий собой дифференциальное уравнение первого порядка, не разрешенное относительно производной. Разрешая его относительно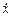 
, получаем уравнение в разделяющихся переменных, интегральными кривыми которого являются окружности:
.
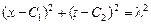Учитывая граничные условия, находим, что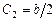 
, а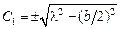 
. Не нарушая общности, можем считать, что интересующая нас дуга окружности не больше ее половины, тогда центр окружности лежит ниже ос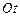и 
, и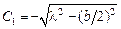 
. Для определения параметра 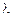, то есть радиуса искомой окружности, используем условие постоянства периметра.
.
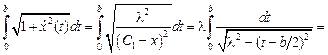
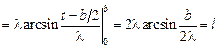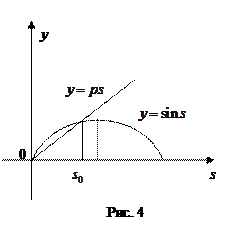Уравнение 
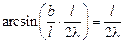эквивалентно уравнению 
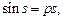где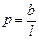 
, 
, 
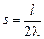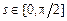. Из геометрических соображений ясно, что задача содержательна лишь при условии 
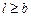, следовательно, 
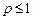, а тогда уравнение 
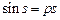всегда имеет на отрезке 
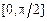единственный корень 
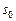(рис. 4).
Отсюда находим радиус искомой окружности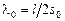 
и координаты ее центра: 
.
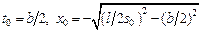Задача о брахистохроне
Предположим, что точк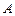и 
и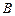 
лежат в плоскости 
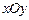с осью 
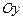, направленной вниз (рис.5). Положим 
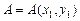и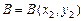 
и пусть 
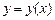– уравнение дуги, соединяющей точк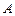и и 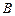так, что 
, 
, 
, 
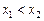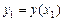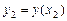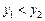. Скорость движения вдоль кривой пусть равна 
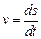. Тогда время спуска равно
.
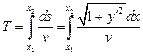Чтобы найти скорость v как функцию координаты x, воспользуемся законом сохранения энергии:
,
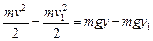где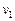 
— начальная скорость движения частицы. Тогда
,
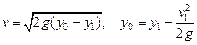и задача свелась к выбору функции 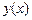, для которой интеграл
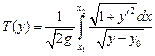
достигает наименьшего значения из всех возможных.
Так как функция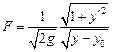 
зависит только от 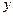и 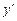, то уравнение Эйлера допускает первый интеграл:
.
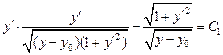Разрешая это уравнение относительно 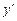, находим
,
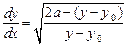где мы положили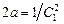 
. Таким образом, мы получили дифференциальное уравнение первого порядка в разделяющихся переменных. Решая его, имеем:
.
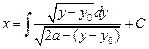Для вычисления интеграла удобно воспользоваться заменой
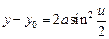. Тогда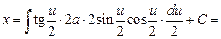 
.
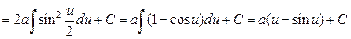Мы пришли к решению в параметрической форме
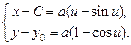
Это и есть кривая наибыстрейшего спуска, известная под названием циклоиды. Можно показать, что выбор постоянных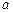 
и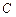 
позволяет провести циклоиду через произвольные две заданные точки. Напомним, что величина 
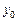не является произвольной постоянной.
Список рекомендуемой литературы
1. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление / Л.Э. Эльсгольц. – М.: Эдиториал УРСС, 2000. – 319 с.
2. Романко В.К. Курс дифференциальных уравнений и вариационного исчисления / В.К. Романко. – М., СПб.: Физматлит, 2000. – 342 с.
3. Пантелеев А.В. Вариационное исчисление в примерах и задачах / А.В. Пантелеев. – М.: Изд-во МАИ, 2000. – 227 с.
Варианты заданий
Задание 5
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе.
1. 
,
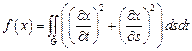– сектор круга: 
.
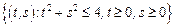Граничные условия: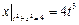 
, 
.
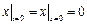2. 
,
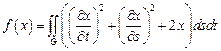– кольцо: 
.
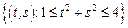Граничные условия: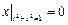 
, 
.
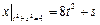3. 
,
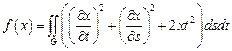– круг: 
.
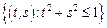Граничные условия: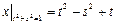 
.
4. ,
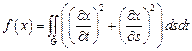– квадрат: 
.
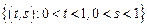Граничные условия: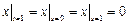 
, 
.
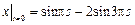5. ,
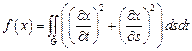– сектор кольца: 
.
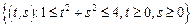Граничные условия: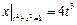 
, 
.
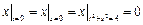6. ,
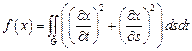– сектор круга: 
.
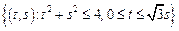Граничные условия: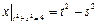 
, 
.
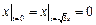7. 
,
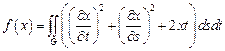– кольцо: 
.
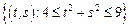Граничные условия: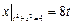 
, 
.
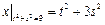8. 
,
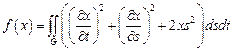– круг: 
.
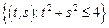Граничные условия: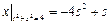 
.
9. ,
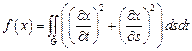– квадрат: .
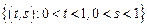Граничные условия: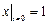 
, .
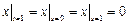10. 
,
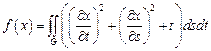– сектор кольца: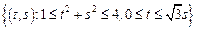 
.
Граничные условия: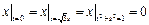 
, 
.
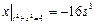11. 
,
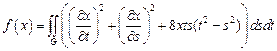– сектор круга: 
.
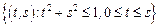Граничные условия: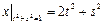 
, 
.
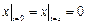12. 
,
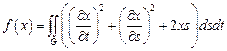– кольцо: 
.
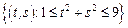Граничные условия: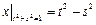 
, 
.
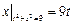13. ,
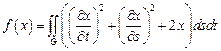– круг: 
.
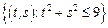Граничные условия: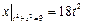 
.
14. 
,
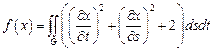– квадрат: .
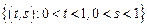Граничные условия: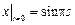 
, 
, 
.
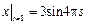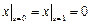15. 
,
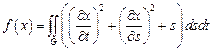– сектор кольца: 
.
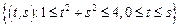Граничные условия: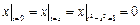 
, 
.
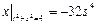16. ,
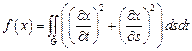– сектор круга: 
.
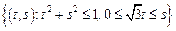Граничные условия: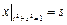 
, 
.
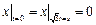17. 
,
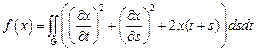– кольцо: .
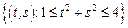Граничные условия: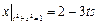 
, 
.
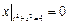18. 
,
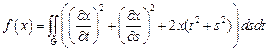– круг: .
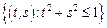Граничные условия: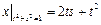 
.
19. ,
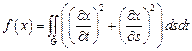– квадрат: .
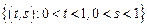Граничные условия: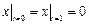 
, 
, 
.
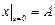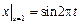20. 
,
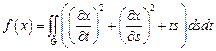– сектор кольца: .
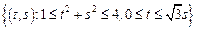Граничные условия: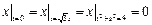 
, 
.
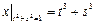21. ,
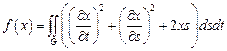– сектор круга: 
.
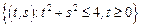Граничные условия: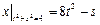 
, .
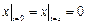22. 
,
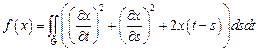– кольцо: .
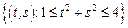Граничные условия: ,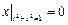 
.
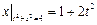23. 
,
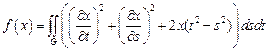– круг: .
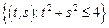Граничные условия: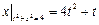 
.
24. ,
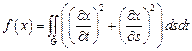– квадрат: .
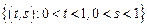Граничные условия: ,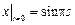 
, 
.
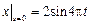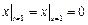25. ,
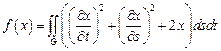– сектор кольца: 
.
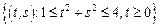Граничные условия: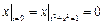 
, 
.
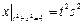26. ,
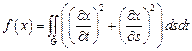– сектор круга: 
, 
.
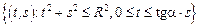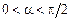Граничные условия: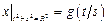 
, 
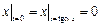, где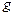 
– произвольная непрерывная на отрезке 
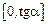функция.
27. ,
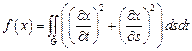– кольцо: .
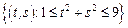Граничные условия: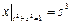 
, 
.
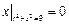28. ,
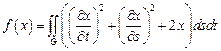– круг: .
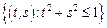Граничные условия: .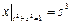
29. ,
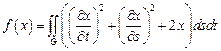– квадрат: .
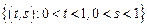Граничные условия: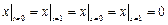 
.
30. 
,
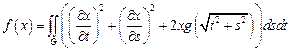– сектор кольца: 
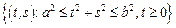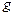, – непрерывная на отрезке 
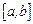функция.
Граничные условия: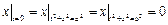 
.
Задание 6
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе, используя для построения решения функции Бесселя и многочлены Лежандра.
1. 
,
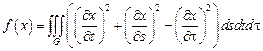– прямой круговой цилиндр: 
.
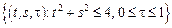Граничные условия: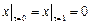 
, 
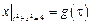, где 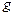– непрерывная на отрезке 
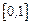функция.
2. 
,
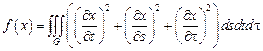– прямой круговой цилиндр: 
.
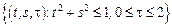Граничные условия: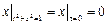 
, 
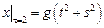, где 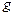– непрерывная на отрезке 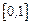функция.
3. ,
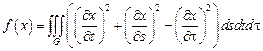– прямой круговой цилиндр: .
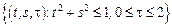Граничные условия: 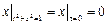, , 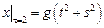где 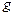– непрерывная на отрезке 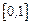функция.
4. ,
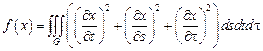– шар: 
.
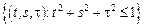Граничные условия: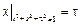 
.
5. ,
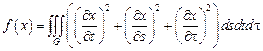– шар: 
.
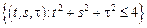Граничные условия: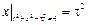 
.
6. ,
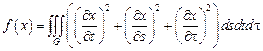– шар: .
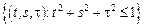Граничные условия: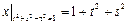 
.
7. ,
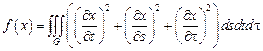– шар: .
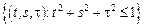Граничные условия: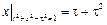 
.
8. ,
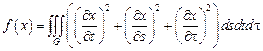– шар: .
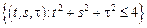Граничные условия: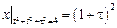 
.
9. 
,
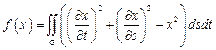– круг: .
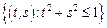Граничные условия: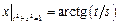 
.
10. 
,
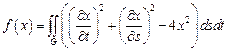– сектор круга: .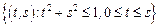
Граничные условия: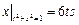 
, .
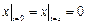11. 
,
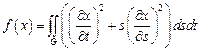– квадрат: .
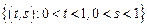Граничные условия: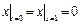 
, 
, 
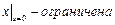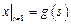, где 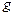– непрерывная на отрезке 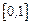функция.
12. 
,
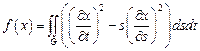– квадрат: .
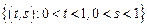Граничные условия: 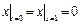, , 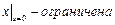, 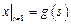где 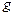– непрерывная на отрезке 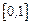функция.
13. ,
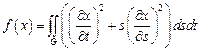– прямоугольник: 
.
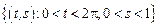Граничные условия: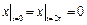 
, , 
,
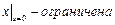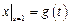где 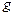– непрерывная на отрезке 
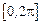функция.
14. ,
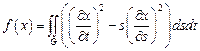– прямоугольник: .
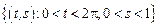Граничные условия: , , ,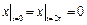
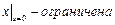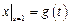где 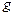– непрерывная на отрезке 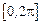функция.
15. 
,
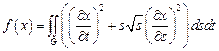– квадрат: .
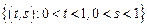Граничные условия: 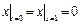, , 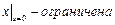, 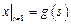где 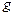– непрерывная на отрезке 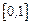функция.
16. 
,
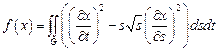– квадрат: .
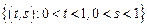Граничные условия: 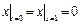, , 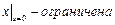, 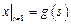где 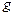– непрерывная на отрезке 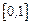функция.
17. ,
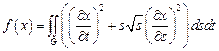– прямоугольник: .
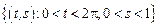Граничные условия: , , ,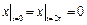
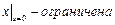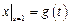где 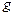– непрерывная на отрезке 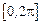функция.
18. ,
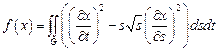– прямоугольник: .
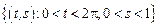Граничные условия: , , ,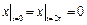
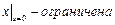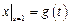где 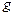– непрерывная на отрезке 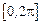функция.
19. 
,
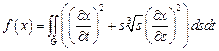– квадрат: .
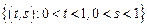Граничные условия: 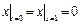, , 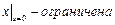, 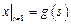где 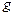– непрерывная на отрезке 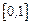функция.
20. 
,
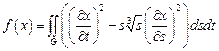– квадрат: .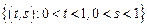
Граничные условия: 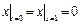,