Основные уравнения математической физики

К основным уравнениям математической физики относятся следующие уравнения в частных производных второго порядка, которые являются частными случаями уравнения (1.88).

Волновое и телеграфное уравнения

Уравнение

,

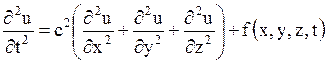(1.102)

где 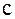- скорость распространения волны в данной среде, называется волновым уравнением.

В приведенном уравнении 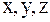обозначают декартовы координаты точки, 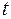- время.

Для двумерного пространства (плоский случай) волновое уравнение имеет вид

.

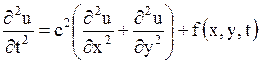(1.103)

В одномерной области уравнение (1.102) принимает вид

.

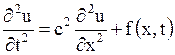(1.104)

Волновое уравнение описывает процессы распространения упругих, звуковых, световых, электромагнитных волн, а также другие колебательные явления. Например, волновое уравнение может описать:

а) малые поперечные колебания струны (при этом под 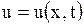понимают поперечное отклонение точки 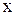струны от положения равновесия в момент времени ; при каждом фиксированном значении график струны 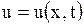на плоскости 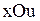дает форму струны в этот момент времени);

б) продольные колебания упругого стержня ( - продольное отклонение частицы от ее положения при отсутствии деформации);

в) малые упругие колебания плоской пластины, мембраны;

г) течение жидкости или газа в коротких трубах, когда трением о стенки трубы можно пренебречь ( - давление или расход).

Уравнение вида

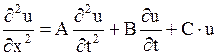(1.105)

называется телеграфным уравнением. Оно описывает электрические колебания в проводах ( - сила тока или напряжение), неустановившееся течение жидкости или газа в трубах ( - давление или скорость).

Волновое и телеграфное уравнения входят в группу уравнений гиперболического типа.

Уравнение теплопроводности

Уравнение вида

,

(1.106)

где - параметр, учитывающий физические свойства изучаемой среды, называется уравнением теплопроводности.

Оно имеет вид для плоского случая

,

(1.107)

для одномерного

.

(1.108)

Уравнением теплопроводности описываются процессы нестационарного массо- и теплообмена. В частности, к этим уравнениям приводят задачи о неустановившемся режиме распространения тепла (при этом означает коэффициент температуропроводности, а - температуру в любой точке исследуемой области в любой момент времени ); о фильтрации упругой жидкости в упругой пористой среде, например, фильтрация нефти и газа в подземных песчаниках ( - коэффициент пьезопроводности, - давление в любой точке среды); о неустановившейся диффузии ( - коэффициент диффузии, - концентрация); о течении жидкости в магистральных трубопроводах ( - давление или скорость жидкости).

Если при рассмотрении этих задач окажется, что в исследуемой области функционируют внутренние источники и стоки массы или тепла, то процесс описывается неоднородным уравнением

,

(1.109)

где функция характеризует интенсивность функционирующих источников.

Уравнения (1.106)…(1.109) являются простейшими уравнениями параболического типа.