Принципы составления математических моделей в нефтегазовой отрасли

Лекция 2

Основные понятия

Через и обозначим скорость движения частицы. Причем, если движение установившееся, то и (х) = и, где х — расстояние от движущейся точки до некоторого начала х = 0. При такой записи задается зависимость (функциональная) скорости движущейся точки от ее положения, т. е. от значения местонахождения частицы (ее расстояние от начала отсчета х — 0). При помощи и = и (х) можем определить ее скорость. Так, например, при свободном падении частицы массой т с высоты h в среде, сопротивлением которой пренебрегаем, скорость частицы в зависимости от ее положения определяется формулой

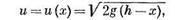
где х — расстояние частицы от поверхности земли (от начала отсчета х = 0).

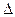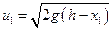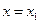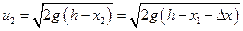Задаваясь различными значениями х, в формуле (1.2) можно найти скорость падающей частицы на различных расстояниях от поверхности земли. При определении скорости частицы в различных ее положениях (ее расстояниях от поверхности земли) х = х₁; х = х₂ и т. д. достаточно в формуле (1.2) х заменить x₁ ,x₂ и т. д. Если, например, х₂ = х₁ + х, то по формуле (1.2) —скорость частицы в положении , а скорость частицы в положении х₂ = х₁ + 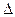х .

Таким образом, и = и (х) или и = f (x) определяет скорость частицы, находящейся на расстоянии х от начала отсчета. Точно также и = и (х + 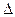х) определяет скорость той же частицы на расстоянии х + 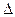х от начала отсчета. Изменение скорости частицы при переходе из положения х в положение х + 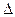х определится равенством

.

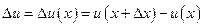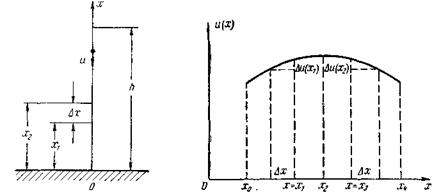
Рис. 1. Рис. 2.

В дальнейшем 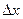будем называть приращением функции, а 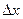— приращением аргумента. При этом малым значениям 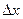соответсвутуют малые значения 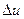. Другими словами, если 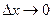, то и .

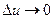Следует отметить, что 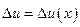также является функцией х, т. е. при одном и том же приращении 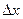приращения функции для различных точек 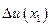и 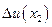не будут равны. Чтобы показать последнее, рассмотрим формулу (1.2) для точек 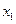= 5м и 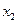= 8л. Пусть h = 10 м и 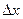= 0,2 м. Тогда

,

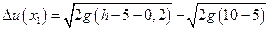а

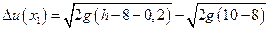, т.е.

.

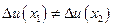Так как в дальнейшем примем 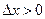, то остановимся на определении знака приращения функции .

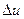Если и 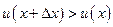, т. е., например, скорость в точке 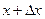больше, чем в точке х, то 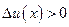и скорость точки возратает. Если же 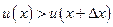, т. е. значение функции (в нашем примере значение скорости) в точке х больше, чем в точке 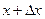, то 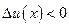, и рассматриваемая функция убывает.

Таким образом, во всем интервале, где 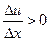, функция и (х)

возрастает, а где - 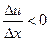—она убывает. На рис. 2 в интервале 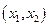функция и (х) возрастает, и, следовательно, во всех точках этого интервала - 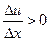, а в интервале (х₂; х₃) она убывает и, следовательно, 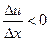. Отношение - 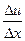- характеризует быстроту изменения функции в зависимости от х на отрезке 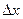. Чтобы найти характер изменения и (х) в данной точке х, следует вычислить

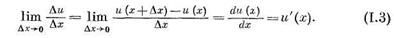
Формула (1.3) характеризует быстроту изменения и (х) в зависимости от х. Она дает производную от функции и (х) по аргументу х. Если функция и = и(х) есть зависимость скорости от положения движущейся точки, то - 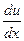— дает значение градиента скорости и в направлении оси х, т. е. характеризует быстроту (и характер) изменения скорости. Если —— 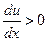, то скорость и(х) на пути х возрастает, если же 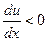, то она убывает.

Чем больше абсолютная величина 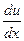, тем больше изменения скорости в данной точке х. Таким образом, если на каком-либо интервале 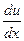положительная величина, то это означает возрастание функции и(х), а если отрицательная величина, то—убывание. Если же в какой-либо точке х = х₂ имеет место 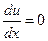, то в этой

точке функция и(х) достигает или своего максимума (точка перехода от возрастания к убыванию), или же своего минимума (точка перехода от убывания к возрастанию).

При неустановившемся движении, когда скорость движущейся частицы не только изменяется при переходе из одной точки в другую, но и в каждой точке изменяется во времени, обозначим через 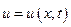скорость точки, находящейся на расстоянии х от начала отсчета в момент времени t. Точно также через 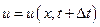обозначим скорость частицы той же точки, но в момент времени 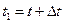. Таким образом, 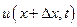будет означать скорость точки, находящейся на расстоянии 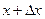от начала отсчета в момент времени t, и, наконец, 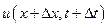— скорость частицы в точке 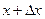в момент времени .

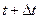Следует особо отметить, что в общем случае величины 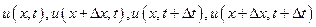между собой не равны, но они все будут стремиться к величине 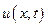при 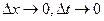. В нашем примере 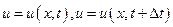соответствуют значениям скорости частицы, находящейся на расстоянии х от начала отсчета в моменты времени t и 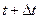. Поэтому 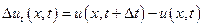есть приращение скорости частицы в данной точке х за промежуток времени 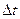. Точно также 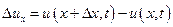есть разность скоростей частиц, характеризующихся в точках 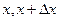в момент времени t. Другими слонами, 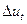характеризует изменение скорости во времени в данной фиксированной точке ж, а 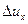— изменение скорости в данный момент времени t в различных точках х и х + Ах. При этом 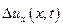и 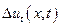будут зависеть от х и t.

Если 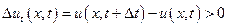, то в данной точке х скорость частицы со временем растет, если же 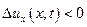, то она убывает.

Точно также, если 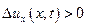, то скорость в точке 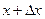в данный момент времени t больше, чем и точке х, если же 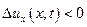, то скорость в точке х больше, чем в точке 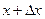. Заметим, что и в этом случае при 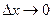величина 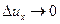и при 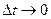величина .

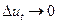Характер изменения 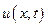в различных точках 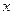в данный момент времени t выражается формулой

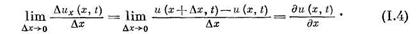
Это равенство представляет собой частную производную от функции 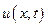по 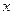в данный момент времени t, которая характеризует измененение функции (ее возрастание или убывание, а также быстроту изменения) вдоль оси х в данный момент времени t.

Точно также

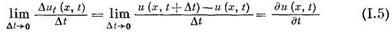
есть частная производная от функции 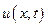по времени t в фиксиро-ишшой точке 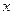, которая характеризует поведение функции и (х, t) (возрастание и убывание и быстроту изменения во времени в рассматриваемой точке ).

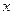Таким образом, если 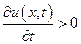, то во всех рассматриваемых точках функция 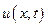во времени растет, если же 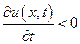,то - убывает. Точно также, если 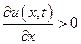, то в данный момент времени t вдоль оси х функция и (х, t) растет, если же 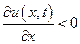, то—убывает.

Еще раз отметим, что при помощи формулы (1.4) определяется изменение скорости (функция 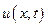вдоль оси 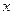в данный фиксированный момент времени t, а при помощи формулы (1.5) — изменение скорости (функция и (х, t) во времени в данной фиксированной точке х. Другими словами, при получении формулы (1.4) время t считаем фиксированным, а при получении формулы (1.5) значение х считается фиксированным. Поэтому

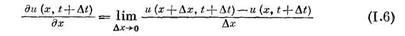
означает изменение скорости (функции и (х, t) вдоль оси х в данный момент времени 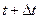. Причем при 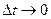формулы (1.4) и (1.6) совпадают. Точно также

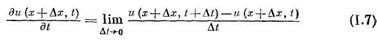
означает изменение скорости (функции и (х, t) во времени в данной фиксированной точке 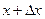. Причем при 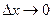формулы (1.7) и (1.5) совпадают.

Из математического анализа известно, что, если

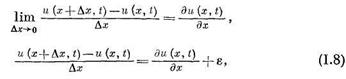
где 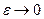при 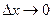, т. е. при малых значениях 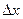величина 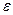сколь угодно мала.

Перепишем (1.8) в виде

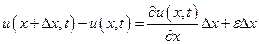. (1.9)

Так как 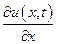величина конечная и не зависящая от ,

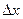то при малых значениях 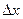второй член в правой части формулы (1.9), т. е. 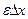, есть малая величина более высокого порядка,

чем первый член - 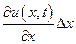. Поэтому, пренебрегая величиной 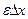по

сравнению с - 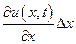и обозначая 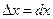для значений 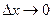, из формулы (1.9) получаем

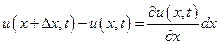(1.10)

Аналогичноиз (1.7) получим

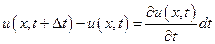(1.11)

Ниже приводятся некоторые сведения из векторного исчисления, необходимые при дальнейшем изложении материала.

Векторная величина а определяется в общем случае тремя проек­циями на оси декартовой системы координат, т. е.

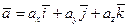
где 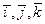— единичные векторы соответственно осей х, у и z. Величину а находим по формуле

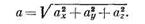
Градиент скалярной величины 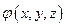(grad) является векто­ром, направленным по нормали к поверхности 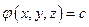. Например, в случае плоскорадиальной фильтрации несжимаемой жидкости (одиночная цилиндрическая скважина в центре круглого цилин­дрического пласта) градиент давления направлен по радиусу, так как поверхности равного давления — цилиндрические окружности. Градиент скалярной величины выражается формулой

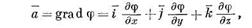
где 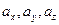— проекции вектора а соответственно на оси 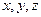и, следовательно,

Широко применяется в нефтепромысловой механике и понятие скалярной величины — дивергенции векторной величины с

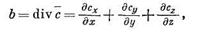
где с_х, с_у и с_г — проекции на оси х, у и z.

Исходя из определения дивергенции и градиента имеем

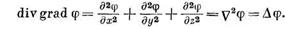
Знак 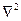(набла в квадрате), или 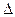(дельта), носит название оператора Лапласа.

Закон сохранения массы

В этом разделе рассматривается вывод уравнения неразрывности (сплошности) для различных случаев движения однородной и неоднородной жидкостей, являющегося математическим выражением закона сохранения (постоянства) массы. В общем случае движения скорость и, плотность 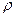и давление р являются функциями координат х, у, z, -. движущейся частицы и времени t, т. е.

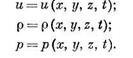
При этом и (х, у, z, t) — скорость жидкости в каждой данной точке пространства в момент времени t, т. е. она относится к определенным точкам пространства, а не к определенным частицам жидкости, передвигающимся в пространстве. То же самое относится к 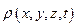и р (х, у, z, t).

Несжимаемая жидкость

Рассматривается одномерное движение жидкости в трубе (рис. 3) вдоль оси х. Считая жидкость несжимаемой, принимаем, что в ней невозможно образование пустот, т. е. соблюдается условие неразрывности (сплошности) движения. Исходя из этого, количество жидкости,

Рис. 3.

проходящей в единицу времени через сечения 1—1 (G_1x) и 2—2 (G._2x), должно быть одинаково, т. е.

G_1x = G_2x. (I.12)

Обозначим через 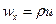массовую скорость в направлении оси х, где 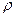— плотность рассматриваемой жидкости. Так как масса жидкости в рассматриваемом объеме не изменяется, то массовая скорость во всех сечениях будет одна и та же, т. е.

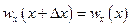. (I.13)

Следовательно,

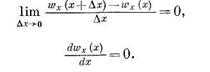
Формула (1.14) выражает закон сохранения массы при одномерном течении жидкости. Исходя из формулы (1.13)или же (1.14), имеем w_x = const, т. е. с учетом постоянства плотности получается 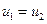, где и₁ — средняя скорость в сечении 1—1, а и₂ — в сечении 2—2.

При выводе уравнения (1.14) предполагается, что площадь поперечного сечения трубы постоянная. В противном случае, обозначая площадь поперечного сечения 1—1 через F₁, а площадь 2—2 — через F₂ и учитывая, что

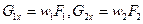, (I.15)

из формулы (1.12) получаем

u₁F₁ = u₂F₂ (I.16)

Из формулы (1.16) видно, что при установившемся течении несжимаемой жидкости средние скорости в поперечных сечениях обратно пропорциональны площадям этих сечений.

Так как при установившемся течении газа массовый расход по длине трубы имеет одно и то же значение, то, исходя из (1.12) и (1.15), для установившегося течения газа получаем

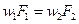
или же

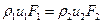. (I.17)

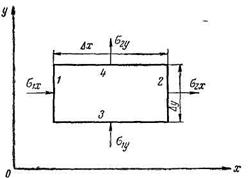
Рис. 4.

Рассмотрим случай плоского течения несжимаемой жидкости. Для этого возьмем параллелепипед со сторонами 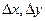, 1 объемом 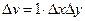(рис. 4). Количество жидкости, протекающей через стороны 1, 2, 3 и 4 соответственно будет ,

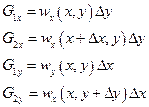где w_x и w_y — массовые скорости в направлениях осей ох и оу. Заметим, что на рис. 4 не ограничиваем направление течения. Жидкость может притекать через грани 1 и 4 и вытекать через грани 2,3 или же притекать через грани 1 и 2 и вытекать через грани 3,4. Также возможны и другие направления течения. Однако количество притекающей жидкости должно быть равно количеству вытекающей жидкости. Это объясняется тем, что рассматриваемая жидкость несжимаемая, т. е. в рассматриваемом объеме масса (плотность) жидкости не изменяется. Если, например, G_1x = 7; G_2x = 3 и G_l =5, то в силу несжимаемости жидкости со стороны 4 должно вытекать G_2y =9. Другими словами,

(G_2x-G_1x) + (G_2y-G_1y) = 0. (I.18)

Закон сохранения массы [см. формулу (1.18)] показывает, что количество притекающей в данный объем жидкости равно количеству пмтокающей из него жидкости. Выражения в скобках в формуле (1.18) всегда имеют разные знаки, причем здесь приводятся алгебраи­ческие значения G_1x,G_2x,G_1y и G_2y. В нашем примере G_2y-G_1y = 4, а G._2x - G_1x =-4. Последнее замечание имеет место при любом варианте течения. Изменение количества жидкости в рассматриваемом прямоугольнике будет:

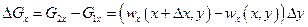; (I.19)

в направлении оси ох и

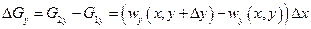(1.20)

в направлении оси оу.

Во всех случаях течения несжимаемой жидкости AG_X и AG_y будут иметь разные знаки и

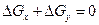. (I.21)

Формула (1.21) получена с учетом того, что количество притека­ющей в рассматриваемый объем жидкости равно количеству вытека­ющей. Подставляя значения 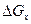и 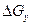из (1.19) и (1.20) в (1.21), получаем

.

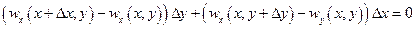Разделив последнее выражение на 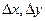и перейдя к пределу при 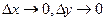, получим

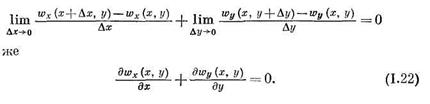
Формула (1.22) выражает закон сохранения массы и называется уравнением неразрывности (сплошности) при плоском течении несжимаемой жидкости. В формуле (1.22) 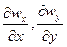всегда имеют разные знаки. Это объясняется тем, что если, например, 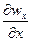отрицательная величина, то w_x убывает, и по направлению ох больше притекает жидкости (через сечение 1), чем вытекает (через сечение 2), что может привести к накоплению жидкости. Поэтому из-за несжимаемости жидкости в направлении оу утечка жидкости должна быть больше ее притока. w_y будет расти вдоль оу, т. е. значение 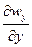должно быть положительным. Точно также при положительной 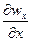утечка жидкости в направлении ох должна компенсироваться ее притоком в направлении оу, следовательно w_y будет убывать, т. е, значение 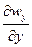должно быть отрицательным. Наконец, рассмотрим течение несжимаемой жидкости в пространстве. Для этого возьмем параллелепипед (рис. 5), грани которого параллельны координатным плоскостям и имеют площади:

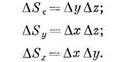
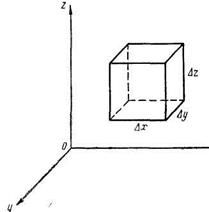
Рис. 5.

Количество жидкости, протекающей через грани взятого параллелепипеда,*определяется по формулам:

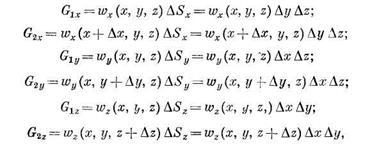
где w_z — массовая скорость в направлении оси z.

Изменение количества жидкости в рассматриваемом параллелепипеде будет в направлении осей :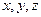

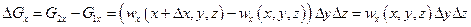
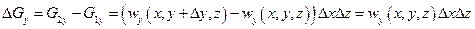
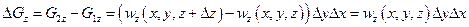
Так как жидкость несжимаемая, то

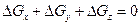(1.23)

В зависимости от направления движения две из этих величин будут иметь одинаковый знак, а третья величина — противополож­ный знак. В противном случае жидкость со всех сторон будет прите­кать в рассматриваемый объем, что физически невозможно из-за несжимаемости жидкости.

Подставив значения 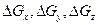в (1.23), разделив их соответственно на 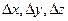и перейдя соответственно к пределу при 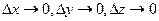, получим

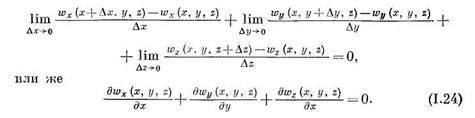
Формула (1-24) выражает закон сохранения массы и называется уравнением неразрывности (сплошности) при пространственном течении несжимаемой жидкости. При получении уравнения (1.24) предполагается, что жидкость несжимаемая, т. е. масса (плотность) жидкости в рассматриваемом объеме не изменяется. Если в (1.24)

значения 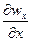, 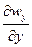имеют одинаковый знак, например положительный, то это означает, что в направлении ох и оу больше вытекает жидкости, чем притекает, так как в этом случае w_x и w_y возрастают. В связи с несжимаемостью жидкости эта утечка должна компенсироваться притоком в направлении oz. По направлению oz приток жидкости в рассматриваемый объем должен быть больше ее утечки из рассматриваемого объема, т. е. w_z будет убывать и,

следовательно, значение 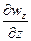должно быть отрицательным.

Сжимаемая жидкость

Если жидкость сжимаемая, т. е. плотность (и, следовательно, масса) жидкости может изменяться во времени, то изменение количества жидкости в рассматриваемом объеме приведет к изменению плотности (массы) жидкости в том же объеме. Так, например, для сжимаемой жидкости (см. рис. 3) 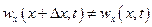и за некоторый промежуток времени 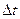разность, между количествами притока жидкости в данный объем и утечки из него приведет к изменению плотности жидкости в рассматриваемом объеме. При этом если 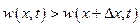, т. е. в данный объем больше притекает жидкости, чем из него вытекает, то это приведет к увеличению плотности в данном объеме, если же 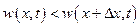, то количество вытекающей из данного объема жидкости больше количества притекающей в него жидкости, что и приведет к уменьшению плотности жидкости в данном объеме. Таким образом, если в течение некоторого промежутка времени 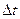величина 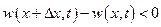, то плотность в данном объеме возрастает, т. е.

,

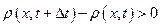если же

,

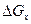
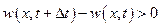то плотность в данном объеме убывает, т. е. .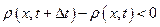

Следовательно, возрастание массовой скорости w (х, t) в данном объеме за некоторый промежуток времени 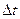приводит к убыванию плотности жидкости в данном объеме, а убывание массовой скот рости приводит к возрастанию плотности в данном объеме. Другими словам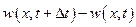и, и 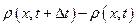всегда будут

иметь противоположные знаки, т. е. знаки 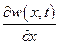, 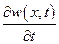будут

разные. Таким образом, если для несжимаемой жидкости ,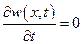

то для сжимаемой жидкости 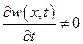. При этом если ,

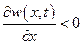то w (x, t) вдоль оси х убывает, т. е. больше притекает жидкости в данный объем, чем из него вытекает, что приводит к возраста-

нию плотности 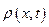во времени, или же 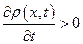Точно

также, если 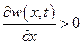, то w (x, t) возрастает вдоль оси х, т. е.

больше вытекает жидкости из данного объема, чем в него притекает, что приводит к убыванию плотности 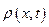во времени,

или же .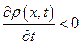

Проиллюстрируем сказанное выше на примерах.

Обозначим через 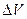объем и положим, что 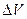= 50 м³. Пусть количество притекающей за время 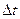в этот объем жидкости будет G₁, а количество вытекающей жидкости G₂. Изменение массы в данном объеме за время 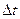обозначим через 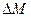. Тогда:

а) если G₁ = 20 кг, a G₂ = 19 кг, т. е. в указанный объем больше притекает жидкости, чем вытекает, то масса жидкости увеличивается на

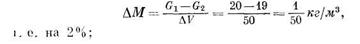
б) если G_x = 20 кг, a G₂ = 21 кг, т. е. из этого объема больше вытекает жидкости, чем в него

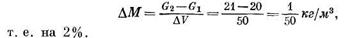
Теперь перейдем к получению математического выражения закона постоянства массы, т. е. к выводу уравнения неразрывности сжимаемой жидкости. Для одномерного движения жидкости (см. рис. 3) изменение количества жидкости 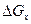за некоторый промежуток времени 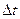составит

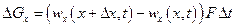, (I.25)

где F — площадь поперечного сечения трубы.

Изменение же массы в рассматриваемом объеме 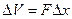за тот же промежуток времени

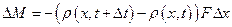. (1.26)

Как было указано выше, 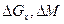всегда будут иметь разные знаки. Приравнивая правые части (1.25) и (1.26), получаем выражение закона постоянства массы

.

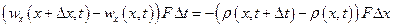В результате деления последнего выражения на 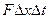при переходе к пределу при 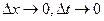находим

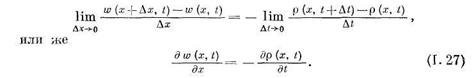
Уравнение (1.27) называется уравнением неразрывности сжимаемой жидкости при линейном течении. Правая часть, т. е. 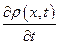, характеризует изменение плотности жидкости 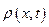во времени, а левая часть 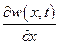—изменение скорости вдоль оси х (оси трубы).

Поэтому 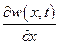, 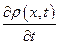всегда будут иметь разные знаки. Уравнение (1.27) справедливо для любой точки 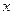ив любой момент времени t. Это объясняется тем, что сечения х и 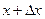, а также моменты времени t и 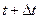были взяты произвольно, а для получения (1.27) мы переходили к пределу при 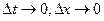, т. е. формула (1.27) была получена для произвольной точки х и произвольного момента времени t. Последнее замечание относится также к случаю плоского и пространственного течения жидкости.

При плоском течении жидкости мы исходили из рис. 4. Изменение количества жидкости за промежуток времени Δt определяли по формуле

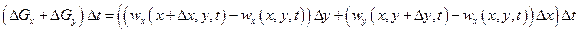, (1.28}

а изменение массы в рассматриваемом объеме — по формуле

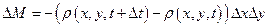. (I.29)

При выводе формул (1.28) и (1.29) рассматриваем параллелепипед с шириной, равной единице, длиной 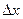; и высотой 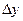. Приравняв, правые части (1.28) и (1.29), предварительно разделив их на 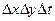,. и перейдя к пределу при 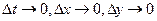, получим

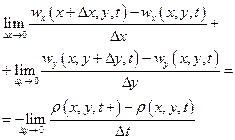
или

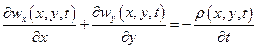^(L30)

Это уравнение называется уравнением неразрывности плоского течения сжимаемой жидкости, и справедливо оно для любой точки (х, у) в любой момент времени t.

Наконец, для получения уравнения неразрывности при течении жидкости в пространстве мы исходили из рис. 5. Изменение количества жидкости в рассматриваемом объеме 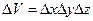за промежуток времени Д£ определяли при помощи равенства

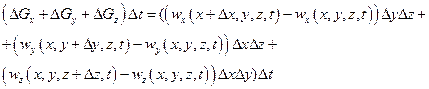(1.31)

Изменение же плотности в рассматриваемом объеме 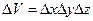в рассматриваемый промежуток времени 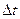будет

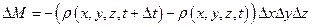. (1.32)

Приравняв правые части (1.31) и (1.32), предварительно разделив их на 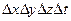, и перейдя к пределу при 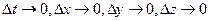, получим

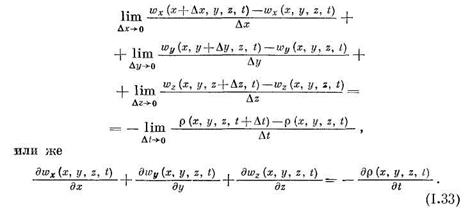
Это уравнение представляет собой уравнение неразрывности при пространственном течении сжимаемой жидкости. Правая часть уравнения 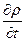——- характеризует изменение плотности во времени,

а левая — изменение количества жидкости в рассматриваемом объеме.

Уравнение (1.33) справедливо для любой точки пространства

(х, у, z) в любой момент времени t. Величины 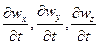могут иметь как одинаковые, так и противоположные знаки. Однако во всех случаях знак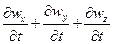и и 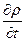будут противоположными. Так, например, если в точках указанного объема значение 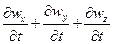положительное (при этом 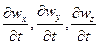все могут быть положительными или иметь разные знаки), то это

значит, что из указанного объема жидкости вытекает больше, чем притекает; последнее приводит к уменьшению плотности в этом

объеме во времени, т. е. 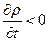. Точно также, если значение

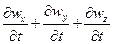отрицательное при этом 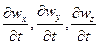все могут быть отрицательными или же иметь разные знаки ), то в данный объем больше притекает жидкости, чем вытекает; последнее приводит к увеличению плотности во времени в этом объеме, и,

следовательно, .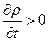

При получении уравнения неразрывности (1.33) подсчитывалось изменение массы в объеме параллелепипеда 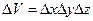. Этот параллелепипед заполненный. Если рассмотреть фильтрацию жидко­сти через однородную пористую среду пористостью т, то объем _г занятый жидкостью, станет равным .

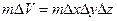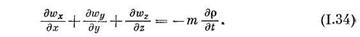Точно также для плоского и одномерного течения из уравнений (1.30) и (1.27) получим следующие уравнения неразрывности плоской и одномерной фильтрации жидкости:

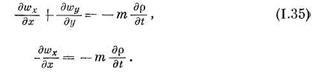Поэтому уравнение неразрывности в этом случае будет

В случае смеси жидкостей и газов, т. е. переменности состава вдоль объема, уравнение неразрывности выводится для двухкомпонентной системы. .Состав смеси определяется массовой концентрацией с — отношением массы данного компонента к общей массе жидкости в заданном элементарном объеме.

Изменение с происходит путем механического перемешивания — состав движущегося объема не меняется, но в каждой заданной неподвижной точке, находящейся в этом месте жидкости, с со временем будет изменяться.

При диффузии под 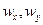понимаются мольные скорости потока, а 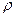будет соответствовать концентрации. Условием диффузии является наличие градиента концентраций диффундирующего компонента (аналогично тому, как температурный градиент является условием теплопроводности). Будем считать, что накапливающая масса вызывает увеличение концентрации компонента 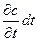. С помощью этого прироста концентрации также можно выразить накапливающуюся и элементарном параллелепипеде массу .

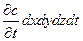Закон сохранения энергии

Покажем на примерах, как можно применять закон сохранения энергии для описания некоторых физических процессов.

В основном будут рассматриваться механический и тепловой процессы, поэтому сформулируем для них закон сохранения энергии. Для механических процессов сумма кинетической и потенциальной энергии постоянна.

При тепловых процессах закон со<