Основные теоретические положения. Закон Ома
Закон Ома, законы Кирхгофа
Основные теоретические положения. Закон Ома
Участок ветви, содержащий один или несколько источников энергии, является активным. Рассмотрим участок электрической цепи (рис. 1.1).
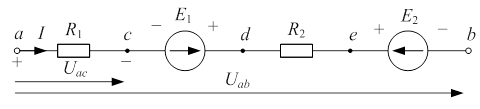 |
| Рис. 1.1 |
При решении задач по теории электрических цепей выбирают положительное направление тока, которое указывается стрелкой.
Направление тока характеризуется знаком тока. Понятия положительный или отрицательный участок имеют смысл, если сравнивать направление тока в проводнике с некоторым заранее выбранным направлением – так называемым положительным направлением тока.
Запомнить!
1) Ток в сопротивлении всегда направлен от более высокого потенциала к более низкому, т.е потенциал падает по направлению тока (на рис. 1.1 условно точке «а» присвоим знак «+», а точке «с» – знак «–»).
2) Э.Д.С., направленная от точки «c» к точке «d», повышает потенциал последней на величину 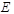 (на рис. 1.1 условно зажиму Э.Д.С., подключенному к точке «c», присвоим знак «–», а зажиму, подключенному к точке «d» – знак «+»).
(на рис. 1.1 условно зажиму Э.Д.С., подключенному к точке «c», присвоим знак «–», а зажиму, подключенному к точке «d» – знак «+»).
3) Напряжение 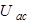 положительно, когда потенциал точки «a» выше, чем потенциал точки «c».
положительно, когда потенциал точки «a» выше, чем потенциал точки «c».
При обозначении напряжения (разности потенциалов) на схемах посредством стрелки она направляется от точки высшего потенциала к точке низшего потенциала.
На рис. 1.1 ток протекает от точки «a» к точке «c», значит, потенциал 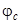 будет меньше
будет меньше 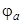 на величину падения напряжения на сопротивлении
на величину падения напряжения на сопротивлении 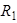 , которое по закону Ома равно
, которое по закону Ома равно 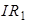 :
: 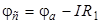 .
.
На участке «c - d» Э.Д.С. 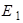 действует в сторону повышения потенциала, следовательно,
действует в сторону повышения потенциала, следовательно, 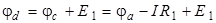 .
.
Потенциал точки «b» равен:
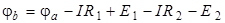 .
.
Знак «–» перед Э.Д.С., совпадающей по направлению с током, объясняется следующим образом: напряжение на участке с Э.Д.С. противоположно направлено самой Э.Д.С. и определяемому напряжению.
Напряжение  найдем как разность потенциалов:
найдем как разность потенциалов:
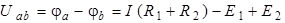 . . | (1.1) |
Ток на участке ab определяют по выражению
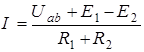 . . | (1.2) |
Формула (1.2) выражает обобщенный закон Ома, или закон Ома для активного участка цепи.
Из формулы видно, что если ток, напряжение и Э.Д.С. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если Э.Д.С. действует в сторону, противоположную положительному направлению тока, в выражении ставится знак «–».
Закон Ома применяется как для участка ветви, так и для одноконтурной замкнутой схемы.
Законы Кирхгофа
Для расчета разветвленных электрических цепей применяют 1–ый и 2–ой законы Кирхгофа. Распределение токов по ветвям электрической цепи подчиняется первому закону Кирхгофа, а распределение напряжений по участкам цепи подчиняется второму закону Кирхгофа.
Законы Кирхгофа наряду с законами Ома являются основными в теории электрических цепей.
Первый закон Кирхгофа:
Алгебраическая сумма токов в узле равна нулю:
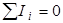 , , | (1.3) |
где 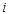 – число ветвей, сходящихся в данном узле, т.е. суммирование распространяется на токи в ветвях, которые сходятся в рассматриваемом узле.
– число ветвей, сходящихся в данном узле, т.е. суммирование распространяется на токи в ветвях, которые сходятся в рассматриваемом узле.
Число уравнений, составляемых по первому закону Кирхгофа, определяется формулой:
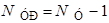 ,
,
где 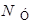 – число узлов в рассматриваемой цепи.
– число узлов в рассматриваемой цепи.
Знаки токов в уравнении берутся с учетом выбранного положительного направления. Знаки у токов одинаковы, если токи одинаково ориентированы относительно данного узла.
Уравнения, составленные по первому закону Кирхгофа, называются узловыми.
Второй закон Кирхгофа:
Алгебраическая сумма Э.Д.С. в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура:
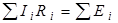 , , | (1.4) |
где 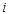 – номер элемента (сопротивления или источника напряжения) в рассматриваемом контуре.
– номер элемента (сопротивления или источника напряжения) в рассматриваемом контуре.
Число уравнений, составляемых по второму закону Кирхгофа, определяется формулой:
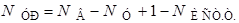 ,
,
где 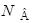 – число ветвей электрической цепи,
– число ветвей электрической цепи, 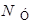 – число узлов,
– число узлов, 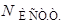 – число источников тока.
– число источников тока.
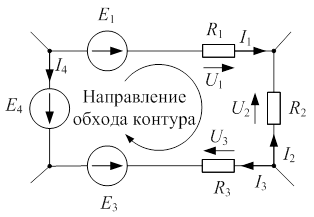 |
| Рис. 1.2 Иллюстрация ко второму закону Кирхгофа |
Для того чтобы правильно записать второй закон Кирхгофа для заданного контура, следует выполнить следующие действия:
1) Произвольно выбрать направление обхода контура, например, по часовой стрелке.
2) Э.Д.С. и падения напряжения, которые совпадают по направлению с выбранным направлением обхода, записываются в выражении со знаком «+»; если Э.Д.С. и падения напряжения не совпадают с направлением обхода контура, то перед ними ставится знак «–».
С учетом вышеперечисленного второй закон Кирхгофа для схемы рис.1.2 запишется следующим образом:
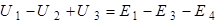 ,
,
или
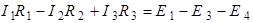 .
.
Уравнения, составленные по второму закону Кирхгофа, называются контурными.
Запомнить! Если цепь содержит источники тока, то при составлении уравнения по второму закону Кирхгофа выбираем контур, в который не входят источники тока.
Примеры расчета линейных электрических цепей по законам Ома и Кирхгофа
Пример 1.1
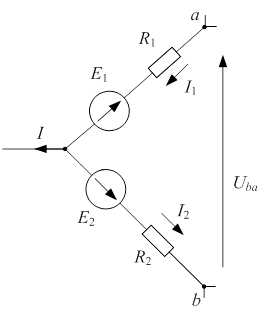 Рис. 1.3 Рис. 1.3 | Для схемы рис. 1.3 определим напряжение 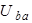 если если 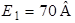 ; ; 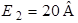 ; ; 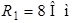 ; ; 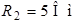 ; ; 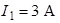 ; ; 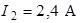 . Решение Запишем формулу для расчета напряжения между узлом «b» и узлом «a» . Решение Запишем формулу для расчета напряжения между узлом «b» и узлом «a» 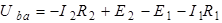 , Подставим численные значения, получим: , Подставим численные значения, получим: 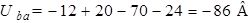 . Ответ: . Ответ: 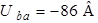 . . |
Пример 1.2
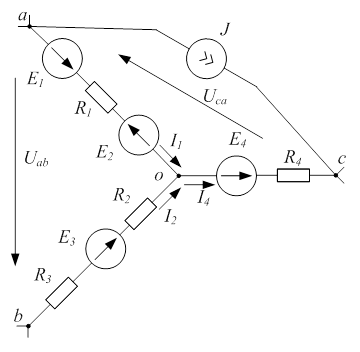 | Для схемы на рис. 1.4 определим напряжения 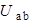 и и 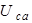 , если , если 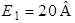 ; ; 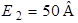 ; ; 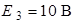 ; ; 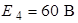 ; ; 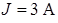 ; ; 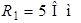 ; ; 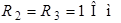 ; ; 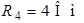 ; ; 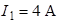 ; ; 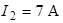 ; ; 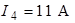 . Решение Используя обобщенный закон Ома для участка цепи, запишем формулы для определения напряжений . Решение Используя обобщенный закон Ома для участка цепи, запишем формулы для определения напряжений  и и 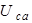 : : |
| Рис. 1.4 |
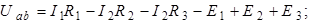
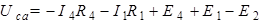 .
.
Подставим численные значения, получим:
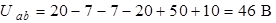 ;
;
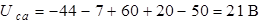 .
.
Ответ: 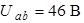 ,
, 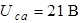 .
.
Пример 1.3
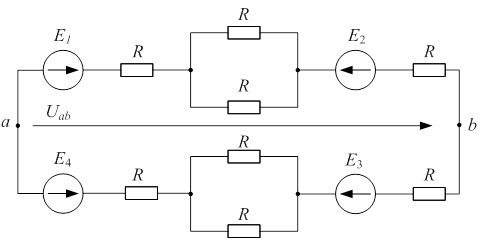 |
| Рис. 1.5 |
Определить  , если известно, что
, если известно, что 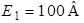 ;
; 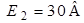 ;
; 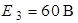 ;
; 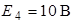 ;
; 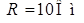 .
.
Решение
Заменим параллельные участки эквивалентными сопротивлениями 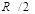 и зададимся положительным направлением тока (рис. 1.6). Напряжение
и зададимся положительным направлением тока (рис. 1.6). Напряжение 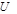 можно определить, рассматривая верхнюю или нижнюю половины контура между точками «а» и «b». В обоих случаях результат должен быть одинаковым.
можно определить, рассматривая верхнюю или нижнюю половины контура между точками «а» и «b». В обоих случаях результат должен быть одинаковым.
Определим ток 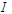 по закону Ома:
по закону Ома:
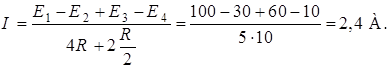
Если рассматривать верхнюю половину контура, то
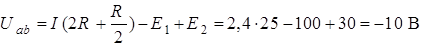 .
.
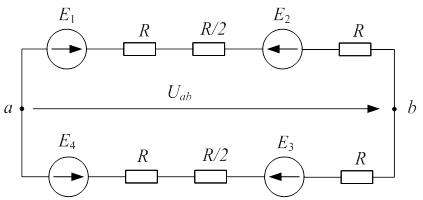 |
| Рис. 1.6 |
Знак «–» говорит о том, что напряжение на данном участке направлено от точки «b» к «a», т.е. потенциал точки «b» больше потенциала точки «a».
Ответ: 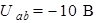 .
.
Пример 1.4
В цепи (рис. 1.7) заданы токи 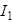 и
и 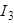 , сопротивления и Э.Д.С. Определить токи
, сопротивления и Э.Д.С. Определить токи 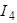 ,
, 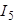 ,
, 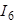 ; напряжение между точками a и b, если
; напряжение между точками a и b, если 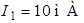
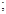
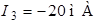 ;
; 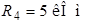 ;
; 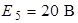 ;
; 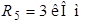 ;
; 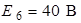 ;
; 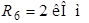 .
.
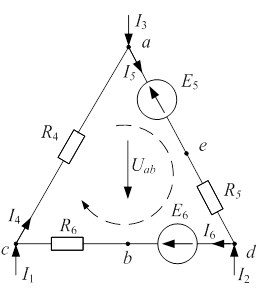 |
| Рис. 1.7 |
Решение
1) Для заданного контура составим два уравнения по первому закону Кирхгофа и одно – по второму. Направление обхода контура указано стрелкой.
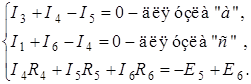
В результате решения получаем: 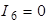 ,
, 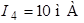 ,
, 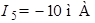 .
.
2) Зададим направление напряжения между точками «a» и «b» от точки «a» к точке «b» –  . Это напряжение найдем из уравнения по второму закону Кирхгофа:
. Это напряжение найдем из уравнения по второму закону Кирхгофа:
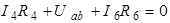 ;
;
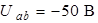 .
.
Ответ: 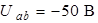 .
.
Метод наложения
Примеры расчета линейных электрических цепей методом наложения
Пример 2.1
Дано: 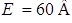
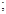
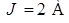
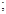
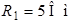
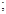
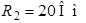
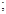
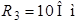
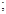
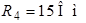 .
.
Определить все токи методом наложения в схеме рис. 2.1.
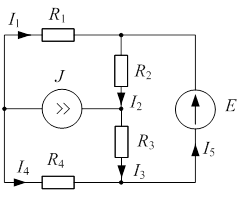 | 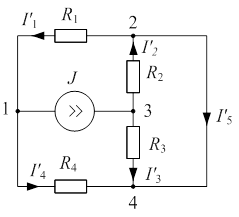 |
| Рис. 2.1 | Рис. 2.2 |
Решение
1) Заменяем источник Э.Д.С. E короткозамкнутым участком (т.к. его 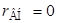 ) (схема рис. 2.2).
) (схема рис. 2.2).
Т.к. конфигурация цепи изменилась, то в цепи рис. 2.2 протекают токи, отличные от токов цепи рис. 2.1. Их называют первыми частичными токами и обозначают одним штрихом. Схему цепи рис. 2.2 более наглядно представим на рис. 2.3. Токи рассчитаем, применяя правило плеч и первый закон Кирхгофа:
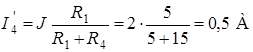 ;
;
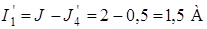 ;
;
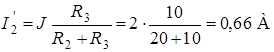 ;
;
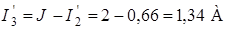 ;
;
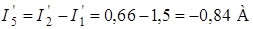 .
.
Ток 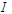 протекает по короткозамкнутому участку (его сопротивление равно нулю).
протекает по короткозамкнутому участку (его сопротивление равно нулю).
Запомнить! Ток в ветви, сопротивление которой равно нулю, определяют по первому закону Кирхгофа.
2) Разорвем ветвь с источником тока J. Токи, протекающие в цепи рис. 2.4, называют вторыми частичными токами и обозначают двумя штрихами.
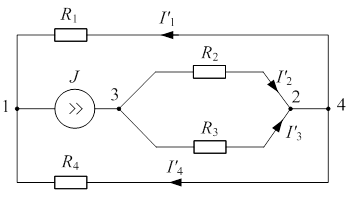 | 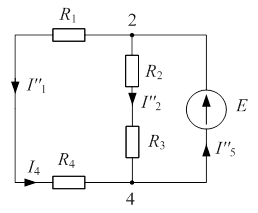 |
| Рис. 2.3 | Рис. 2.4 |
Напряжение, создаваемое Э.Д.С. E, приложено к двум параллельным ветвям. Токи 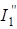 и
и 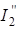 определим по закону Ома:
определим по закону Ома:
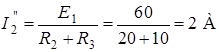 ;
;
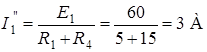 ;
;
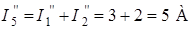 .
.
3) Искомые токи найдем как алгебраическую (т.е. с учетом направлений) сумму частичных токов:
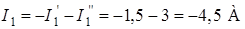 ;
;
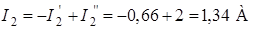 ;
;
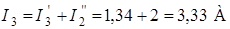 ;
;
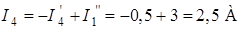 ;
;
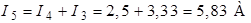 .
.
Ответ: 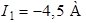 ,
, 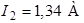 ,
, 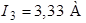 ,
, 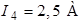 ,
, 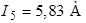 .
.
Метод контурных токов
Примеры расчета линейных электрических цепей методом контурных токов
Пример 3.1
Составить уравнение по методу контурных токов и определить токи во всех ветвях схемы (рис. 3.1), если 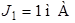 ;
; 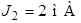 ;
; 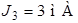 ;
; 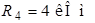 ;
; 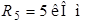 ;
; 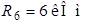 ;
; 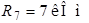 ;
; 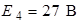 .
.
На примере данной задачи покажем как пользоваться методом контурных токов, если схема содержит источники тока.
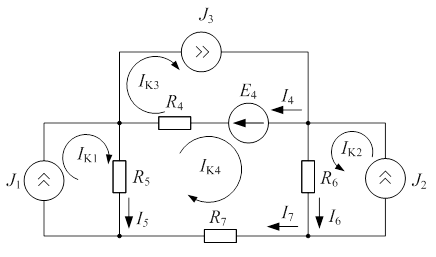 |
| Рис. 3.1 |
Решение
В цепи четыре независимых контура, следовательно обозначим четыре контурных тока: 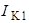 ,
, 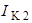 ,
, 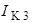 ,
, 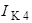 и их положительные направления.
и их положительные направления.
Токи 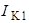 ,
, 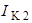 ,
, 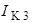 , протекают через источники тока
, протекают через источники тока 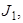
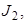
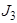 соответственно. Следовательно:
соответственно. Следовательно: 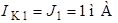 ;
; 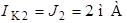 ;
; 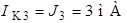 ;
;
В данной задаче необходимо определить один контурный ток 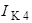 , следовательно, составим только одно уравнение:
, следовательно, составим только одно уравнение:
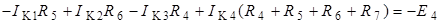 ,
,
Откуда 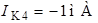 .
.
Токи ветвей определим как алгебраическую сумму контурных токов:
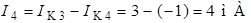 ;
;
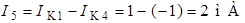 ;
;
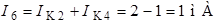 ;
;
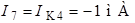 .
.
Правильность решения задачи проверим, составив уравнение по второму закону Кирхгофа для контура 4 (контур обходим по часовой стрелке):
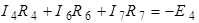 ;
;
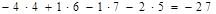 ;
;
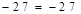 .
.
Второй закон Кирхгофа выполняется.
Ответ: 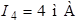 ,
, 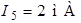 ,
, 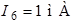 ,
, 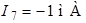 .
.
Пример 3.2
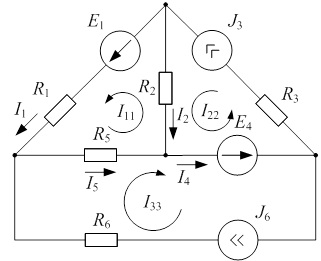 Рис. 3.2 Рис. 3.2 | Дано: 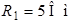 ; ; 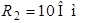 ; ; 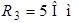 ; ; 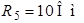 ; ; 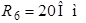 ; ; 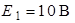 ; ; 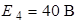 ; ; 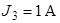 ; ; 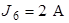 . Определить токи в схеме рис. 3.2 методом контурных токов. Решение Выбираем направления контурных токов. Контурные токи . Определить токи в схеме рис. 3.2 методом контурных токов. Решение Выбираем направления контурных токов. Контурные токи 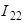 и и 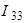 совпадают по направлению с токами источников совпадают по направлению с токами источников 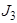 и и 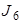 и равны им и равны им |
соответственно: 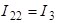 ;
; 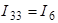 . Для решения задачи необходимо составить одно уравнение для неизвестного контурного тока
. Для решения задачи необходимо составить одно уравнение для неизвестного контурного тока 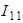 :
:
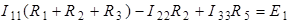 .
.
Решив его, получаем:
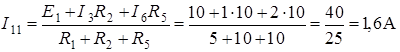 .
.
Токи в ветвях схемы определяем как алгебраическую сумму контурных токов, проходящих через каждую ветвь:
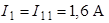 ;
;
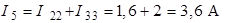 ;
;
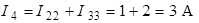 ;
;
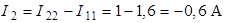 .
.
Ответ: 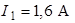 ,
, 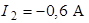 ,
, 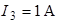 ,
, 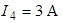 ,
, 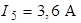 ,
, 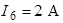 .
.
Метод узловых напряжений
Примеры расчета линейных электрических цепей методом узловых напряжений
Пример 4.1
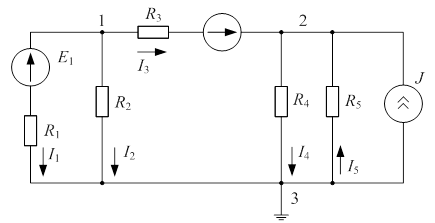 Рис. 4.1 Рис. 4.1 | Дано: 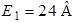 ; ; 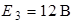 ; ; 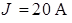 ; ; 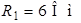 ; ; 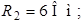 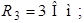 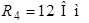 ; ; 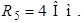 Определить все токи в схеме рис. 4.1 методом узловых напряжений. Определить все токи в схеме рис. 4.1 методом узловых напряжений. |
Решение
Цепь содержит три узла, ветви с идеальными Э.Д.С. отсутствуют. Число необходимых уравнений, определяемое по формуле (4.1), равно двум. В качестве базисного выбираем третий узел.
Система уравнений имеет вид:
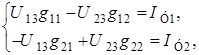 ,
,
где
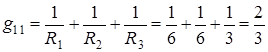 ;
;
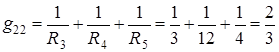 ;
;
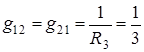 ;
;
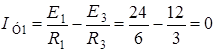 ;
;
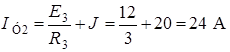 .
.
В результате решения определяем:
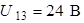 ;
;
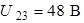 .
.
Токи ветвей определяем по обобщенному закону Ома:
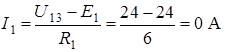 ;
;
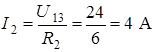 ;
;
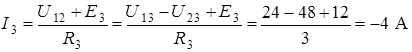 ;
;
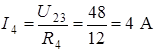 ;
;
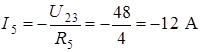 .
.
Правильность решения задачи целесообразно проверить составлением и расчетом баланса мощностей.
Уравнение баланса мощностей:
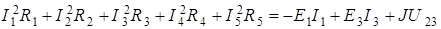 ;
;
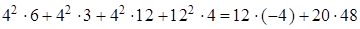 ;
;
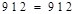 .
.
Мощность приемников равна мощности потребителей, т.е. баланс мощностей выполняется.
Проверим выполнение второго закона Кирхгофа для внешнего контура.
Второй закон Кирхгофа:
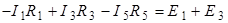 ;
;
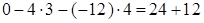 ;
;
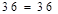 .
.
Ответ: 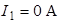 ,
, 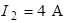 ,
, 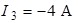 ,
, 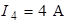 ,
, 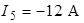 .
.
Пример 4.2
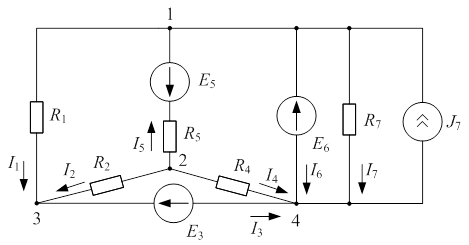 | Дано: 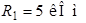 ; ; 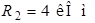 ; ; 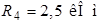 ; ; 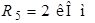 ; ; 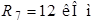 ; ; 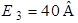 ; ; 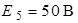 ; ; 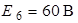 ; ; 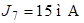 . . |
| Рис. 4.2 |
Определить токи в схеме рис. 4.2 методом узловых напряжений.
Решение
В схеме 4 узла. В ветвях 3 и 6 включены идеальные источники Э.Д.С., эти ветви соединяются в узле 4. По формуле (4.1) определяем число уравнений: 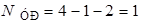 .
.
Действительно, если за базисный узел принять узел 4 (но также можно принять узел 1 или 3), то сразу определяем 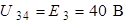 и
и 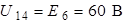 . Неизвестным является узловое напряжение
. Неизвестным является узловое напряжение 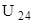 .
.
Уравнение по методу узловых напряжений имеет вид:
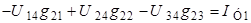 .
.
где
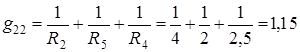 ;
;
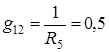 ;
;
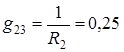 ;
;
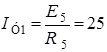 ;
;
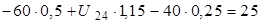 ;
;
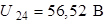 .
.
Определяем токи 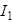 ,
, 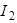 ,
, 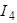 ,
, 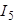 ,
, 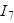 по закону Ома:
по закону Ома:
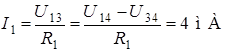 ;
; 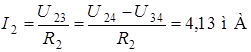 ;
;
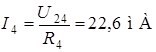 ;
; 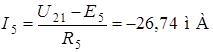 ;
; 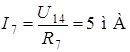 .
.
Токи 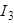 и
и 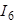 определяем по первому закону Кирхгофа:
определяем по первому закону Кирхгофа:
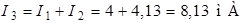 ;
;
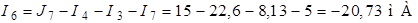 .
.
Ответ: 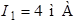 ,
, 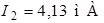 ,
, 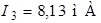 ,
, 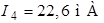 ,
, 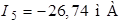 ,
, 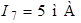 .
.
Пример 4.3
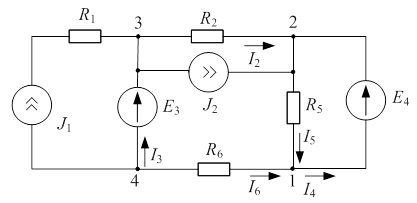 | Дано: 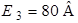 ; ; 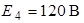 ; ; 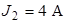 ; ; 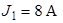 ; ; 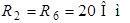 ; ; 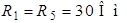 . . |
| Рис. 4.3 |
Решение
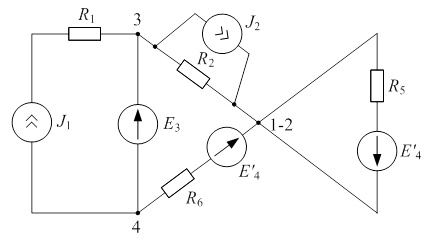
Особенностью схемы является наличие двух ветвей с идеальными источниками Э.Д.С., которые расположены в ветвях, не имеющих общего узла. В этом случае цепь подвергается следующему преобразованию. В одной из ветвей, содержащих идеальный источник Э.Д.С. (например ветвь с 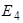 ), включают компенсирующую Э.Д.С.
), включают компенсирующую Э.Д.С. 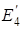 , равную
, равную 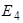 по величине и противоположную по направлению. Точно такая же Э.Д.С.
по величине и противоположную по направлению. Точно такая же Э.Д.С. 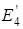 включается во все соседние ветви, сходящиеся в одном из узлов данной ветви. Направления включаемых Э.Д.С.
включается во все соседние ветви, сходящиеся в одном из узлов данной ветви. Направления включаемых Э.Д.С. 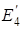 по отношению к этому узлу сохраняется (рис. 4.4). Токораспределение в цепи не изменяется.
по отношению к этому узлу сохраняется (рис. 4.4). Токораспределение в цепи не изменяется.
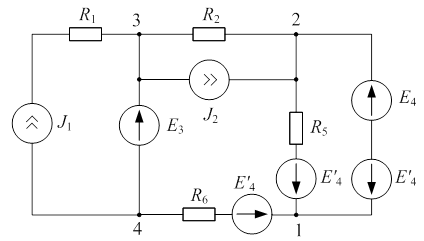 |
| Рис. 4.4 |
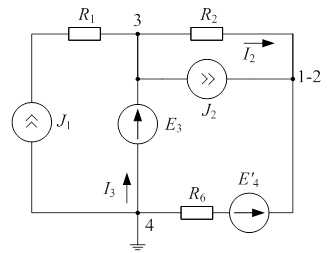
Рисунки 4.5 а, б, в – демонстрируют это преобразование.
Теперь схема (рис. 4.5 в) содержит только одну ветвь с идеальным источником Э.Д.С. 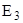 . Потенциалы узлов 1 и 2 равны, т.к. их соединяет короткозамкнутый участок (рис. 4.5 а). Следовательно ветвь с
. Потенциалы узлов 1 и 2 равны, т.к. их соединяет короткозамкнутый участок (рис. 4.5 а). Следовательно ветвь с 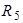 можно удалить из схемы. Примем узел 4 за базисный, тогда
можно удалить из схемы. Примем узел 4 за базисный, тогда
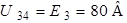 .
.
Уравнение по методу узловых напряжений имеет вид:
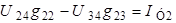 ,
,
где
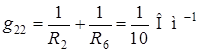 ;
; 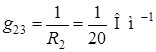 ;
; 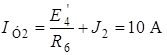 ;
;
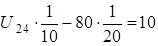 ;
; 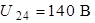 ;
; 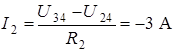 .
.
 |
а
 |
б
 |
| в |
| Рис. 4.5 |
Переходим к исходной схеме (рис. 4.3). Запишем уравнение по 1–ому закону Кирхгофа для узла 3:
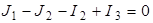 ,
,
откуда
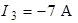 .
.
Запишем уравнение по 1–му закону Кирхгофа для узла 4:
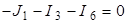 ,
,
откуда
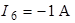 .
.
Ток в ветви 5 определим по закону Ома:
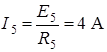 .
.
Ток в ветви с идеальной Э.Д.С. 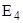 определим по 1–му закону Кирхгофа:
определим по 1–му закону Кирхгофа:
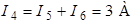 .
.
Ответ: 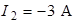 ,
, 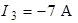 ,
, 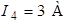 ,
, 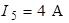 ,
, 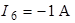 .
.
Пример 4.4
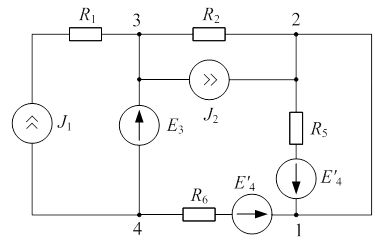
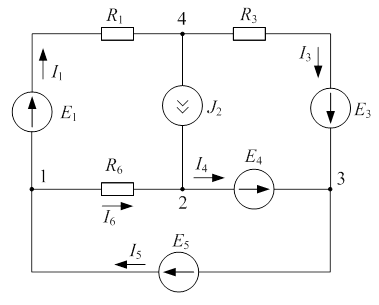 | Дано: 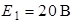 ; ; 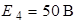 ; ; 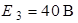 ; ; 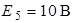 ; ; 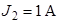 ; ; 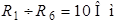 . Определить токи в схеме рис. 4.6 методом узловых напряжений. . Определить токи в схеме рис. 4.6 методом узловых напряжений. |
| Рис. 4.6 |
Решение
За базисный узел в данной схеме можно принимать 1–ый, 2–ой или 3–ий узлы. Рассмотрим решение задачи в случае, если за базисный принят потенциал 3–го узла. Тогда:
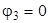 .
.
Поскольку узлы 1 и 2 связаны с 3–им узлом ветвями, содержащими только идеальные источники Э.Д.С. , то:
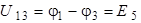 ;
;
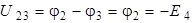 .
.
Остаётся определить потенциал 4–го относительно 3–го базисного. Составляем одно уравнение:
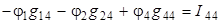 ,
,
где
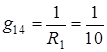 – взаимная проводимость между 1 и 4 узлами;
– взаимная проводимость между 1 и 4 узлами;
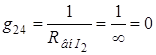 – взаимная проводимость между 2 и 4 узлами;
– взаимная проводимость между 2 и 4 узлами;
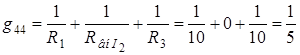 – собственная проводимость 4 узла.
– собственная проводимость 4 узла.
Решаем уравнение:
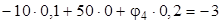 ,
,
откуда:
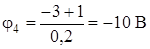 .
.
На основании обобщённого закона Ома для участка цепи, определяем токи:
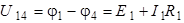 ,
,
откуда
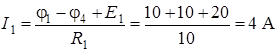 ;
;
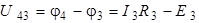 ;
;
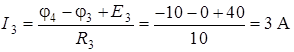 ;
;
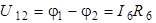 ;
;
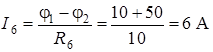 .
.
Токи в четвёртой и пятой ветвях определим по 1–му закону Кирхгофа:
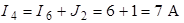 ;
;
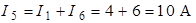 .
.
Ответ: 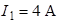 ,
, 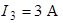 ,
, 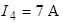 ,
, 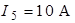 ,
, 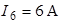 .
.
Пример 4.5
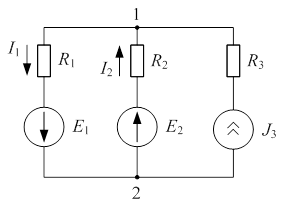 | Дано: 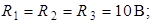 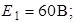 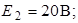 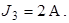 Определить токи в схеме рис. 4.7 методом двух узлов. Определить токи в схеме рис. 4.7 методом двух узлов. |
| Рис 4.7 |
Решение
За базисный принимаем второй узел: 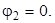 Записываем формулу по методу двух узлов:
Записываем формулу по методу двух узлов:
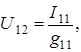
где
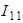 – узловой ток первого узла;
– узловой ток первого узла;
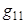 – собственная проводимость первого узла.
– собственная проводимость первого узла.
Тогда
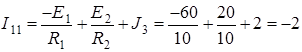 ;
;
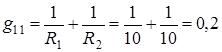 .
.
Внимание! В собственной проводимости первого узла 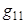 отсутствует слагаемое
отсутствует слагаемое 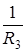 , так как ветвь, содержащая идеальный источник тока, имеет бесконечно большое сопротивление, а значит её проводимость будет стремиться к нулю.
, так как ветвь, содержащая идеальный источник тока, имеет бесконечно большое сопротивление, а значит её проводимость будет стремиться к нулю.
Определим напряжение 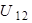 :
:
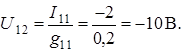
Используя обобщенный закон Ома для участка цепи запишем:
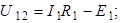
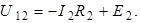
Следовательно, токи в цепи определяются по следующим формулам:
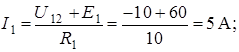
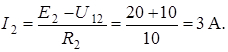
Ответ: 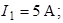
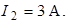
Примеры расчета линейных электрических цепей методом эквивалентного генератора
Пример 5.1
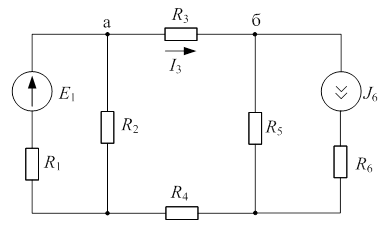 | Дано: 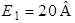 ; ; 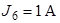 ; ; 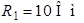 ; ; 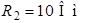 ; ; 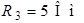 ; ; 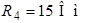 ; ; 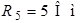 ; ; 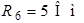 . Определить ток . Определить ток 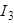 на схеме рис. 5.3 методом эквивалентного генератора напряжения. на схеме рис. 5.3 методом эквивалентного генератора напряжения. |
| Рис. 5.3 |
Решение
Согласно методу об эквивалентном генераторе напряжения ток 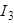 определим по следующей формуле:
определим по следующей формуле:
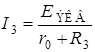 ,
,
где 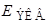 – величина, равная напряжению х.х., возникающему между точками разрыва искомой ветви;
– величина, равная напряжению х.х., возникающему между точками разрыва искомой ветви;
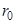 – внутреннее сопротивление Э.Д.С., равное эквивалентному сопротивлению пассивной цепи относительно точек разрыва.
– внутреннее сопротивление Э.Д.С., равное эквивалентному сопротивлению пассивной цепи относительно точек разрыва.
В соответствии с алгоритмом расчета МЭГ:
1) Размыкаем ветвь, ток которой определяем (рис 5.4). Искомая цепь после разрыва ветви 3 изменила свою конфигурацию и состоит из двух независимых контуров, в каждом из которых протекает соответствующий ток.
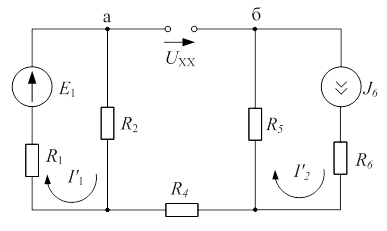 |
| Рис. 5.4 |
Ток 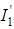 определяем по закону Ома:
определяем по закону Ома:
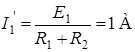 .
.
Ток 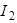 равен току источника
равен току источника 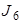 :
: 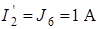 .
.
Напряжение 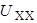 определяем по второму закону Кирхгофа:
определяем по второму закону Кирхгофа:
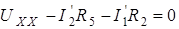 ;
;
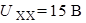 .
.
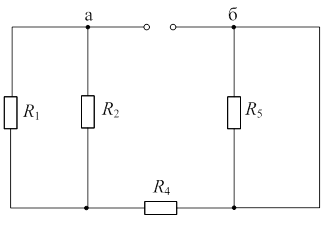 | 2) Определяем 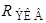 пассивной цепи относительно точек «а» и «б» (рис. 5.5). При этом целесообразно изобразить пассивную схему согласно вышеизложенному правилу: пассивной цепи относительно точек «а» и «б» (рис. 5.5). При этом целесообразно изобразить пассивную схему согласно вышеизложенному правилу: 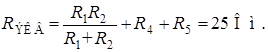 |
| Рис. 5.5 |
3) С учетом рассчитанных 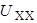 и
и 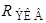 :
: 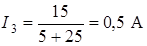 .
.
Ответ: 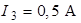 .
.
Пример 5.2
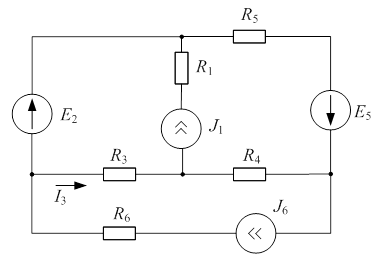 | Дано: 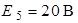 ; ; 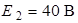 ; ; 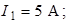 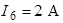 ; ; 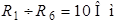 . Определить ток . Определить ток 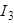 методом эквивалентного генератора напряжения в схеме рис. 5.6. методом эквивалентного генератора напряжения в схеме рис. 5.6. |
| Рис. 5.6 |
Решение
Определим ток в сопротивлении 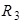 методом эквивалентного генератора напряжения.
методом эквивалентного генератора напряжения.
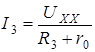 .
.
1) Определим напряжение холостого хода по схеме рис 5.7
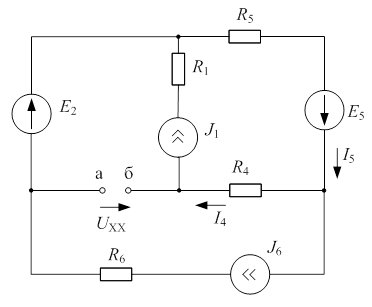 |
| Рис. 5.7 |
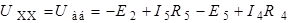 ,
,
где
