Корреляционная функция между входом и выходом объекта.
Корреляционная функция R(τ) случайной функции x(t) - есть среднее значение произведения двух значений этой функции, сдвинутых на определенный промежуток времени, т.е
Rx(τ) = M[x(t) x(t+τ)]
Вследствие инерционности любой САУ случайный процесс не может изменяться бесконечно быстро, т.е. текущее значение случайной функции x(t) не является совершенно не зависимой величиной, а в какой-то степени в среднем зависит от предшествующего ее значения или, как говорят, коррелировано с ним. Корреляционная функция служит мерой этой зависимости.
Основные свойства корреляционной функции стационарного случайного процесса:
1) корреляционная функция является четной функцией, т.е. R(τ)=R(-τ);
2) при τ=0 корреляционная функция дает средний квадрат случайной величины
3) убывающая;
4) при τ→∞ корреляционная функция обращается в квадрат среднего значения случайной величины.
5) чем более подвижен объект, тем быстрее убывает корреляционная функция. Чем быстрее убывает корреляционная функция, тем более высокие частоты содержаться в случайном процессе.
Корреляционная функция суммы двух стационарных случайных процессов характеризует взаимную связь двух случайных процессов между собой в моменты времени, отстоящие друг от друга на промежуток времени τ.
Для определения корреляционной функции изменим модель (рис. 10).
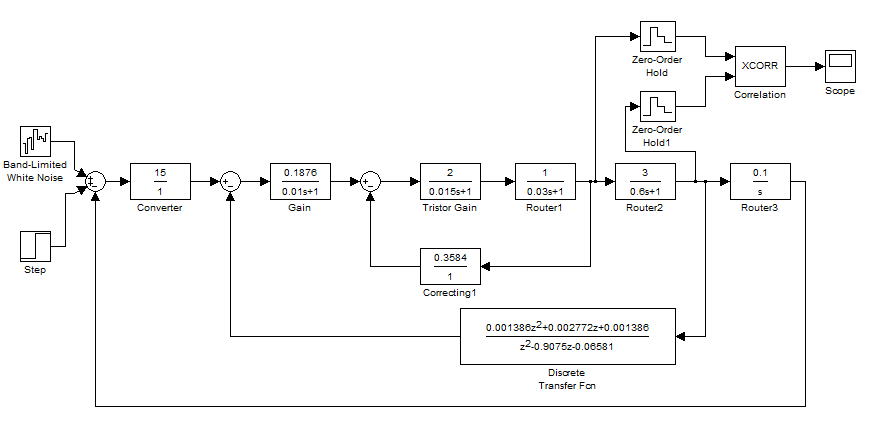
Рисунок 10 - Модель САУ для измерения корреляционной функции между входом и выходом объекта
Корреляционная функция, которую можно посмотреть через блок Scope, имеет вид, представленный на рис. 11.
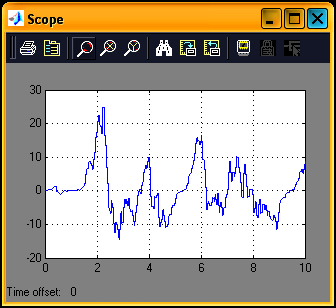
Рисунок 11 - Корреляционная функция между входом и выходом объекта управления
График позволяет сделать вывод о нестационарности процесса. Стационарные процессы обладают свойством эргодичности, для него с вероятностью 1 выполняется, что всякое среднее по множеству равно соответствующему среднему по времени. По графику можно сделать вывод о быстром изменении выходного сигнала. Зная корреляционную функцию и входной сигнал, мы можем рассчитать выходной сигнал в любой момент времени. Коэффициент усиления объекта будет приблизительно равен 0
Корреляционная функция между ошибкой управления и выходной координатой системы
Для получения корреляционной функции используем следующую модель САУ (рис. 12).
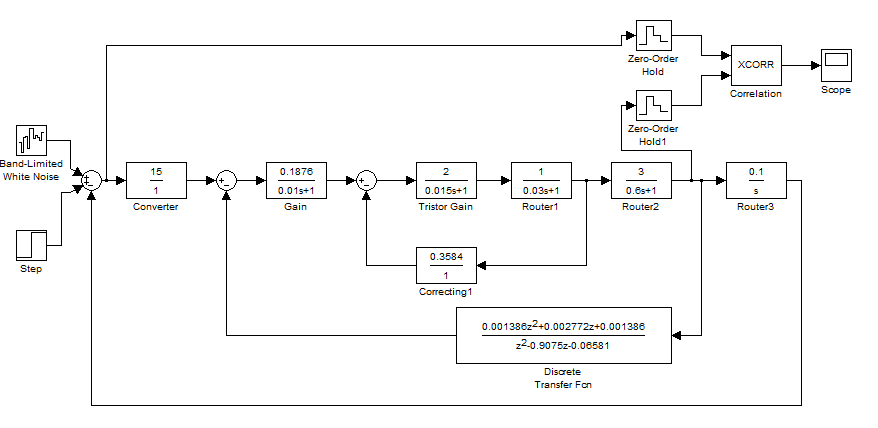
Рисунок 12 - Модель САУ для получения корреляционной функции между ошибкой и выходом объекта
График полученной корреляционной функции показан на рис. 13. Отметим, что её среднее значение колеблется около 0. Это говорит о том, что взаимосвязь между ошибкой и выходной координатой имеет случайный характер, содержит скрытую периодичность и этот процесс является стационарным.
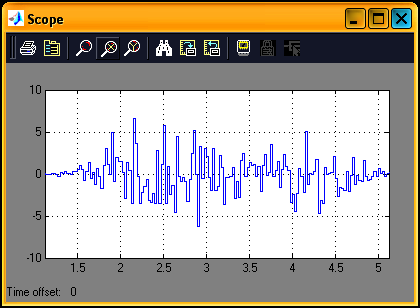
Рисунок 13 - Корреляционная функция между ошибкой управления и выходной координатой
Заключение
В ходе курсовой работы была смоделирована САУ приводом робота-манипулятора. Разработаны две модели для реакции на аналоговый и цифровой входные сигналы. Модель позволяет предсказать поведение системы при воздействии сигналов разного характера, определить характеристики САУ: передаточную функцию, переходную функцию, АФХ, АЧХ, ФЧХ, запасы устойчивости и прочие характеристики. Модель разработана средствами Matlab 6.5.0.1. Модель полностью удовлетворяет всем требованиям к ней.
Литература
1. Дорф, Р. Современные системы управления / Р. Дорф,
Р. Бишоп. – М.: Лаборатория Базовых Знаний, 2002. – 832с.
2. Дьяконов, В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник / В. Дьяконов, В. Круглов – СПб.: Питер, 2002. – 448с.
3. Бакаев, В.Н. Теория автоматического управления. Учебное пособие / В.Н. Бакаев. - Вологда: ВоГТУ, 2009. – 56 с.
Приложение А
Расчеты в среде Matlab
>>[num,den]=linmod('shema_3');
tf(num,den)
Transfer function:
0. 3 s^2 + 4.38 s + 4.38
-------------------------------------------------------------------
0.002 s^5 +0.1 s^4 +1.4 s^3 + 3.4 s^2 + 4.3 s
>> [A,B,C,D]=tf2ss(num,den)
A =
1.0e+007 *
-0.0000 -0.0033 -0.1733 -3.9403 -9.6332 -6.6908 0
1 0 0 0 0 0 0
0 1 0 0 0 0 0
0 0 1 0 0 0 0
0 0 0 1 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 1 0
B =
C =
1.0e+007 *
0.0000 -0.0000 -0.0000 -0.0000 0.0625 5.7901 5.7901
D =
>> F1=A*B;
F2=(A^2)*B;
F3=(A^3)*B;
F4=(A^4)*B;
F5=(A^5)*B;
F6=(A^6)*B;
PC=[B F1 F2 F3 F4 F5 F6];
dp=det(PC)
rp=rank(PC)
dp =
rp =
>>F1=A'*C';
F2=((A')^2)*C';
F3=((A')^3)*C';
F4=((A')^4)*C';
F5=((A')^5)*C';
F6=((A')^6)*C';
Q=[C' F1 F2 F3 F4 F5 F6];
dq=det(Q)
rq=rank(Q)
dq =
rq =
>> sys=tf([0.2081],[0.0108 1 1])
Transfer function:
0.2081
------------------
0.0108 s^2 + s + 1
>> c2d(sys,0.025,'tustin')
Transfer function:
0.001386 z^2 + 0.002772 z + 0.001386
------------------------------------
z^2 - 0.9075 z - 0.06581
Sampling time (seconds): 0.025
