Вывод уравнения фильтрации однофазного флюида для трёхмерной декартовой сеточной модели залежи углеводородов.
Уравнение формулируется для произвольного элемента, с объёмом 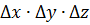 , целочисленными координатами по 3-м декартовым направлениям:
, целочисленными координатами по 3-м декартовым направлениям:
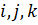
С одной стороны, определяется изменение массы флюида в элементе за счёт перетоков по координатным направлениям:
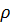 – плотность,
– плотность, 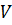 – скорость
– скорость
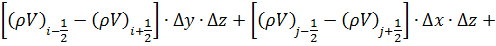
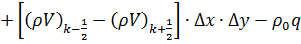 (1)
(1)
здесь 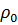 – плотность флюида в нормальных условиях.
– плотность флюида в нормальных условиях.
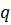 – объёмный дебит (н.у.) через перфорационные отверстия скважины, если они присутствуют в элементе, имеет знак + если сток, знак - если источн.
– объёмный дебит (н.у.) через перфорационные отверстия скважины, если они присутствуют в элементе, имеет знак + если сток, знак - если источн.
С другой стороны, изменение массы флюида внутри элемента за единицу времени на отрезке 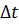 :
:
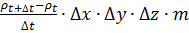 (2)
(2)
По закону сохранения масс выражение (1) = (2) – уравнение массопереноса. Далее приводится к дифференциальной форме делением на объём элемента и предельным переходом при 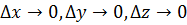 :
:
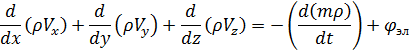
здесь 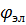 - плотность источников (стоков), полученная как
- плотность источников (стоков), полученная как
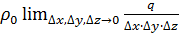
Более компактная дифференциальная форма:
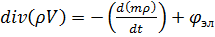 (3)
(3)
Разделив (3) на 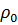 и введя обозначение
и введя обозначение 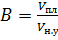 - объёмный коэффициент, где
- объёмный коэффициент, где 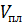 - объём флюида в пластовых условиях,
- объём флюида в пластовых условиях, 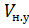 - объём флюида в нормальных условиях.
- объём флюида в нормальных условиях.
Уравнение (3) примет окончательную форму:
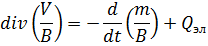
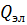 - объёмная плотность источников (стоков), приведённая к нормальным условиям
- объёмная плотность источников (стоков), приведённая к нормальным условиям
/Проверить: 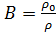 /
/
Выражения объёмных коэффициентов:
Газ: 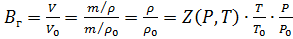
Нефть: 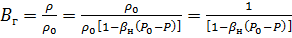
Вода: 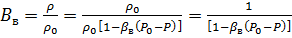
Здесь 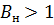 , так как в пласте газ растворён в нефти,
, так как в пласте газ растворён в нефти,
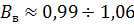 из-за малой сжимаемости.
из-за малой сжимаемости.
4. Краевые и начальные условия для трёхмерного уравнения фильтрации однофазного флюида.
Уравнение фильтрации решается в форме конечных алгебраических уравнений, составляющих систему (1) = (2) для каждого блока сетки, т.е. количество уравнений равно количеству блоков.
Если залежь замкнута, то для приграничных элементов расход флюида через какую-либо грань (одну или более) – нулевой
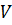 = 0, через грань контура залежи.
= 0, через грань контура залежи.
Для залежи, окружённой водным бассейном, вместо соответствующего расхода флюида в уравнение подставляется расход воды: 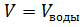
Условия на начало моделирования – распределение по блокам давлений (Р) и значений флюидонасыщенностей (S) считываются с данных предшествующего этапа моделирования, либо с геомодели исходной информации, как в пункте 2.
5. Последовательность прямых расчётов истории эксплуатации залежи выполняется с шагом по времени 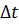 . Используя известное распределение P, S на начало шага
. Используя известное распределение P, S на начало шага 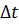 находят решение системы уравнений массопереноса на конец шага при известных значениях дебитов скважин.
находят решение системы уравнений массопереноса на конец шага при известных значениях дебитов скважин.
Прямые расчёты выполняются для сопоставления расчётных P, S с данными промысловых наблюдений и последующей корректировки параметров модели (k, m). Последнее называют идентификацией модели.
Для получения достаточно хорошей сходимости расчётных и промысловых данных приходится выполнять много повторов моделирования истории эксплуатации залежи. Но это необходимо, чтобы принять фильтрационную модель как адекватную и использовать для дальнейших прогнозных расчётов.
Задание:
Ответить на вопросы.
1. Как геометрически представляется трёхмерная сеточная модель в декартовых координатах.
2. Из каких источников выбирают данные для оцифровки сеточной модели.
3. Какой закон природы отображает уравнение фильтрации флюида.
4. Вывести уравнение массопереноса флюида для трёхмерной декартовой сеточной модели.
5. Объяснить окончательную компактную дифференциальную форму уравнения фильтрации, используемую в литературных источнаках, с объёмными коэффициентами.
6. Через какую искомую функцию выражаются объёмные коэффициенты.
7. Что представляют краевые и начальные условия моделирования фильтрации.
8. Для чего необходимо провести моделирование истории эксплуатации залежи.
