Модели разработки залежи нефти при естественных режимах - замкнутый упругий и упруговодонапорный. Режим поддержания давления.

Для поддержания пластового давления вытеснения нефти используется заводнение нефтяных пластов. В России 90% всей нефти добывается из заводняемых месторождений.

Применяются различные виды: внутриконтурное при рядных, блоково-рядных и площадных схемах расположения скважин и законтурное. Используют также очаговое и избирательное заводнение.

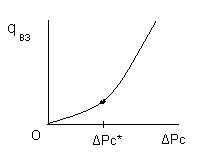
Теория заводнения нефтяных пластов показывает, что расход воды q_вз, закачиваемы в нагнетательную скважину, согласно закону Дарси, должен быть пропорционален перепаду давления на забое 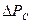. На практике линейная зависимость бывает до некоторого малого перепада 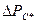, далее расход воды резко нелинейно растет, что объясняют раскрытием трещин, размывом тупиковых зон.

При заводнении нефтяных месторождений сначала добывают безводную нефть, затем нефть с водой.

Если q_вз – дебит закачиваемой воды,

q_в – дебит добываемой воды,

q_н – дебит нефти,

то к моменту времени «t» имеем следующие показатели:

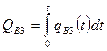- накопленное количество закаченной воды

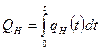- накопленная добыча нефти

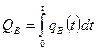- накопленная добыча воды

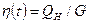- текущая нефтеотдача, G – геологические запасы нефти.

Обычно 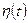рассматривается в зависимости от относительных величин:

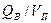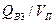или , где V_П - объем пор пласта.

Типичный вид зависимости:

η_о – безводная нефтеотдача.

Извлекаемые запасы нефти:

.

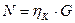Текущая обводненность продукции:

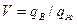, где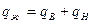

Типичная зависимость обводненности от :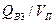

Определим коэффициент вытеснения η₁ нефти водой:

,

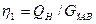где G_ЗАВ – запасы нефти в части пласта, охваченной заводнением.

Определим коэффициент охвата заводнением:

.

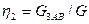Тогда, очевидно, коэффициент текущей нефтеотдачи η определяется :

.

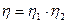Чтобы прогнозировать показатели разработки нефтяного месторождения при его заводнении необходимо использовать модель процесса заводнения и построить для конкретной системы разработки расчетную схему для месторождения в целом.

Рассмотрим расчет показателей разработки на модели поршневого вытеснения.

Прямолинейный пласт, толщиной h, длиной l, шириной b, пористостью m, проницаемостью k.

Давление воды, входящей в левый торец – Р₁, в правый – Р₂ . Будем считать постоянным перепад давлений (Р₁ - Р₂).

Поршневое вытеснение означает, что в заводненной области остается постоянная остаточная нефтенасыщенность S_{н ост} .

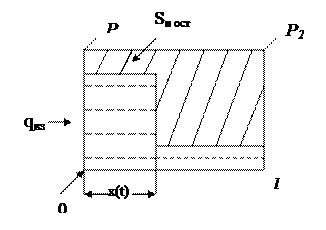
В момент «t» положение фронта вытеснения 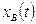. Расход закачиваемой воды .

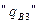Первоначальная водонасыщенность нефтяного пласта связанной (неподвижной) водой S_СВ. Предполагаем, что в обводненной части пласта связанная вода смешивается с поступившей водой. Определим количество закачанной воды в обводненной области :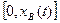

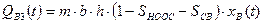Дифференцируя по времени получим с одной стороны расход воды, с другой – скорость движения фронта:

.

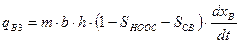С другой стороны по закону Дарси с учетом фазовых проницаемостей воды, нефти: 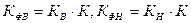, расход воды, закачиваемой в пласт, к моменту t:

,

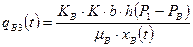где Р_В – давление на фронте.

Не учитывая сжимаемость жидкостей, пород запишем для дебита нефти к тому же моменту t:

.

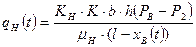Исключая Р_В из уравнения, полученного уравниванием дебитов нефти и воды как несжимаемых жидкостей, 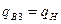, находим:

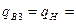
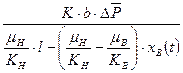, где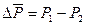

Далее уравниваем дебит, полученный через скорость движения фронта и последние выражение через :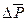

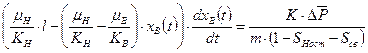
Полученное выражение интегрируется при всех постоянных, кроме 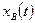с учетом начального условия:

,

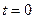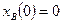
После интегрирования получаем квадратное уравнение:

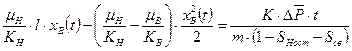
Решая квадратное уравнение находим окончательные формулы для :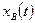

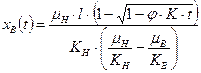, где

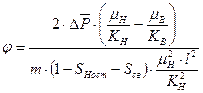
Время полного обводнения пласта находится при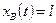

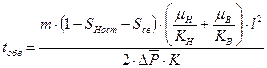
Очевидно, чем больше “К”, тем быстрее обводниться пласт.

Расчет показателей разработки однородного пласта на основе модели двухфазной фильтрации.

Рассмотрим совместную фильтрацию нефть-вода для элемента однорядной схемы, удаленного от скважин, характер течения прямолинейный, жидкости несжимаемые.

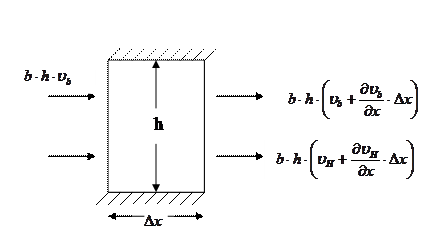
Баланс воды: ,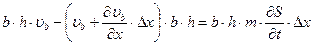

или :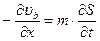

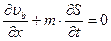
Содержание нефти (1-S),следовательно, баланс нефти:

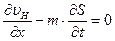
Сложив уравнения, получим:

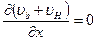, то есть

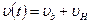, не зависит от “x”

Что следовало ожидать для несжимаемых жидкостей. Это жёсткий водонапорный режим вытеснения нефти водой.

По Дарси:

,

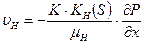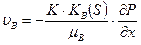
В уравнениях баланса нефти и воды две неизвестных S, P. Неизвестное “P” можно исключить, и составить уравнение, содержащие только “S”.

Составим функцию доли обводнённости в потоке двух жидкостей, то есть расходное содержание воды:

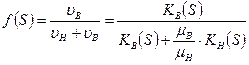
Равенство 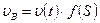дифференцируем по «x»:

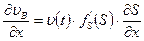
Подставим в уравнение баланса воды:

,

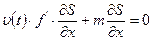которое содержит только «S».