VII. Задачи на смеси и сплавы.
Решение задач на смеси и сплавы вызывают затруднения при решении у многих учащихся. Многие из них такие задачи не решают, а ставят ответы наугад. Поэтому необходимо уделить особое внимание этой теме.
Решение этих задач связано с понятиями «концентрация», «процентное содержание».
Концентрацией вещества называют отношение массы этого вещества к массе всей смеси (раствора, сплава).
Концентрация вещества выражается в процентах. Задачам этого типа уделялось большое внимание в старинных рукописях и «Арифметике» Л.Ф. Магницкого. Старинный способ решения задач позволяет получить правильный ответ.
Задача.
У некоторого человека были продажные масла: одно ценною 10 гривен за ведро, другое 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их, масло ценою 7 гривен за ведро. Какие части этих двух масел нужно взять, чтобы получить ведро масла стоимостью 7 гривен?
Решение:
Друг над другом пишутся стоимости имеющихся масел, слева от них, примерно посередине, стоимость масла, которое должно получиться после смешения. Соединив записанные числа черточками, получим такую схему:
6
7
Рассмотрим пары 7 и 6; 7 и 10; В каждой паре из большего числа вычтем меньшее, результат запишем в конце соответствующей черточки.
Получится такая схема:
6 3
7
10 1
Из этой схемы ясно, что дешевого масла нужно взять втрое больше, чем дорогого. Т.е. для получения одного ведра масла ценою 7 гривен нужно взять дорогого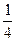 
ведра, а дешевого 
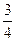ведра.
Обоснование старинного способа решения задач на смеси.
Пусть требуется смешать а%-й и b%-й растворы кислот, чтобы получить с%-й раствор. Пусть х г - масса а%-го раствора, у г – масса b%-го раствора.
г – масса чистой кислоты в 1 растворе.
г – масса чистой кислоты во 2 растворе.
г – масса чистой кислоты в смеси.
Получаем 
, откуда ax + by = c(x +y), сгруппируем слагаемые с х и у, получим (b – c)y = (c – a)x. Отсюда получаем пропорцию:
x : y = (b – c) : (c – a).
Такой же вывод дает схема:
а b - c
с
b c - a
x : y = (b – c) : (c – a).
Современные задачи на смешение тоже могут быть решены этим старинным способом.
Задача:
Имеются два раствора 68% и 78% серной кислоты. Сколько надо взять каждого раствора, чтобы получить 100 г 70%-го раствора серной кислоты?
Изобразим схему:
68 8
70
78 2
Найдем, в каком отношении нужно взять каждого раствора. Из схемы ясно, что 68%-го раствора следует взять 8 частей, 78%-го раствора – 2 части.
100 : 10 = 10г – на 1 часть,
10 
= 80г – 68% кислоты,
10 
= 20г – 78% кислоты.
Аналогично можно решить следующие задачи:
1. Имеются два слитка сплавов меди и олова. Первый содержит 40% меди, второй -32% меди. Какого веса должны быть эти слитки, чтобы после их совместной переплавки получить 8 кг сплава, содержащего 35% меди?
Ответ: 3 кг; 5 кг;
Решение: изобразим схему
40 
3
35
32 5
Из схемы ясно, что первого следует взять 3 части, а второго 5 частей.
3+5=8, 8:8=1кг-на одну часть, следовательно первый слиток должен быть весом 3кг, второй 5кг.
(№800 2006г. Тестовые задания, Кокшетау)
2. Имеется лом стали двух сортов с содержанием никеля в 5 % и 40%. Сколько нужно взять каждого из этих сортов, чтобы получить 140 т стали с содержанием никеля в 30%?
А) 40т; 85т.
В) 40т; 100т.
С) 35т; 150т.
D) 45т; 105т.
Е) 50т; 120.
(Вариант-13 №14 2003г.)
3. Один раствор содержит 30% (по объему) азотной кислоты, а второй 55% азотной кислоты. Сколько нужно взять первого и второго растворов, чтобы получить 100л 50%-ного раствора азотной кислоты?
А) 25л; 75л.
В) 20л; 80л.
С) 40л; 60л.
D) 30л; 70л.
Е) 22л; 78л.
(Вариант-34 №14 2003г.)
(Вариант-14 №17 2006г.)
Коды правильных ответов
| 3кг; 5кг | B | B |
Вот одна из часто встречаемых задач на практике:
Имеется 240г 70%-ного раствора уксусной кислоты. Нужно получить 6% -ый раствор кислоты. Сколько граммов воды (0%-ый раствор) нужно прибавить к имеющемуся раствору?
Решение:
Изобразим схему:
0 64
6
70 6
240 : 6 = 40г составляет одна часть, т.к. из схемы ясно, что уксусной кислоты следует взять 6 частей, воды 64 части.
40 
= 2560г воды.
Ответ: 2560г воды.
Аналогично можно решить задачи, предложенные в тестах при подготовке к ЕНТ.
1. Морская вода содержит 5% соли. Сколько килограммов пресной воды необходимо добавить к морской, чтобы содержание соли в последней составило 4%?
А) 15кг.
В) 20кг.
С) 17кг.
D) 22кг.
Е) 18кг.
(Вариант-31 №30 2003г.)
2. К 15 литрам 10% раствора соли добавили 5% раствор соли и получили 8% раствор. Какое количество литров 5% раствора добавили?
А) 10л.
В) 12л.
С) 15л.
D) 8л.
Е) 7л.
(Вариант-31 №14 2003г.)
3. Морская вода содержит 5% (по массе) соли. К 40 кг морской воды добавили пресной воды и содержание соли в полученной воде составило 2%. Масса добавленной пресной воды равна:
А) 60кг.
В) 16кг.
С) 40кг.
D) 28кг.
Е) 80кг.
(Вариант-35 №2 2004г.)
4. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 5 л морской воды, чтобы концентрация соли составляла 1,5%?
А) 40л.
В) 25л.
С) 42л.
D) 30л.
Е) 35л.
(Вариант-17 №2 2004г.)
5. Морская вода содержит по весу 5% соли. Сколько килограммов пресной воды нужно добавить к 80кг морской, чтобы содержание соли в последней составляло 2%?
А) 122кг.
В) 121кг.
С) 120кг.
D) 123кг.
Е) 130кг.
(Вариант-34 №26 2005г.)
(Вариант-4 №25 2006г.)
6. К 15 литрам 10% раствора соли добавили 5% раствор соли и получили 8% раствор. Какое количество литров 5% раствора добавили?
А) 15л.
В) 10л.
С) 7л.
D) 8л.
Е) 12л.
(Вариант-25 №27 2005г.)
7. Чтобы получить 50% раствор кислоты, надо к 30 г 15%раствора кислоты добавить 75% раствор этой же кислоты. Найти количество 75% раствора кислоты, которое надо добавить.
А) 42г.
В) 6г.
С) 150г.
D) 3г.
Е) 9г.
(Вариант-15 №25 2007г.)
8. Морская вода содержит 5% соли. Сколько килограммов пресной воды нужно добавить к 80кг морской, чтобы содержание соли в последней составляло 4%?
А) 22кг.
В) 15кг.
С) 17кг.
D) 18кг.
Е) 20кг.
(Вариант-14 №25 2007г.)
Коды правильных ответов
| B | A | A | E | C | B | A | E |