V. Тригонометрия на ладони. Решение тригонометрических уравнений.

Для решения некоторых тригонометрических примеров вовсе не обязательно пользоваться формулами. Можно использовать прямоугольный треугольник и четко знать определения синуса, косинуса, тангенса, котангенса.

Например:

1. tg 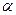= 8\15, .

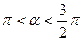Найти sin .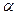

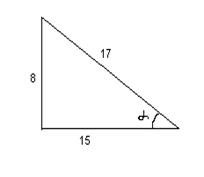
Используем определение синуса острого угла прямоугольного треугольника , что это есть отношение противолежащего катета к гипотенузе, а так же, что синус в третьей четверти отрицательный, получаем: sin = - .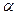

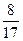2. cos , .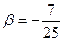

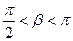Найти: .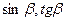

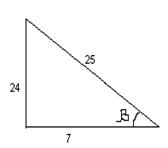
Учитывая определение синуса и тангенса, четверть, в которой лежит угол β, находим: .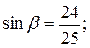

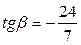3. Найти sin (arcos 2\3).

Применяем формулы:

, .

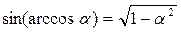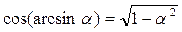sin(arccos ) = .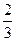

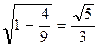4. Вычислите: sin (2arccos a)

Пусть arcсos a равен 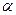, тогда sin 2 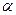= 2 sin 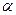cos .

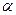Найдем значения sin 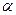, cos 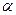и, подставив их в формулу, вычислим.

5. Вычислите: cos (2arcsin a)

Пусть arcsin a равен 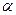, тогда cos 2 = .

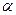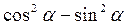Найдем значения sin 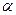, cos 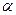и, подставив их в формулу, вычислим.

При решении заданий такого вида важно помнить следующие тождества:

А.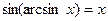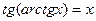
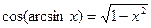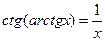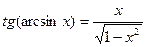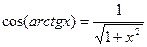Б.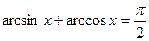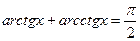
В.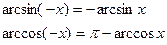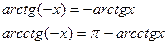
Г.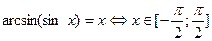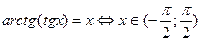

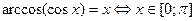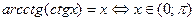Аналогичные задания:

1. Вычислите: cos(2arcsin ).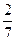

А) 1.

В) .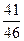

С) .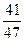

D) .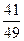

Е) .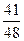

(Вариант-17 №26 2005г.)

2. Вычислите tg 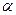, если cos 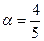, 0 < < .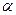

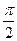А) .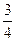

В) .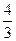

С) .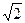

D) .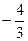

Е) .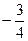

(Вариант-15 №7 2005г.)

3. Вычислите 3ctg 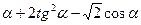, если sin 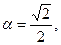0 <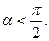

А) 3.

В) 2.

С) -2.

D) 4.

Е) 5.

(Вариант-20 №10 2007г.)

4. Вычислите: cos2 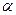, если sin .

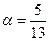А) .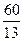

В) .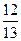

С) .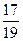

D) .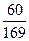

Е) .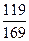

(Вариант-12 №9 2007г.)

5. Вычислите: 2 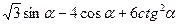, если sin 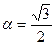, 0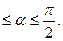

А) 1.

В) 3.

С) 2.

D) 7.

Е) 4.

(Вариант-27 №9 2004г.)

6. Вычислите: sin(2arccos3\5).

А) 0.96.

В) 0.98.

С) 1.

D) 0.97.

Е) 0.99.

(Вариант-32 №28 2006г.)

7. Чему равен cos a, если sin 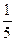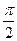a = , < a < ?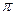

А) .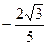

В) .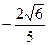

С) .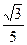

D) .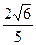

Е) .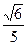

(Вариант-13 №11 2003г.)

8. Вычислите cos 2a, если sin a = .

А) .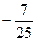

В) .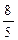

С) .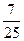

D) - .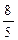

Е) .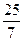

(Вариант-15 №5 2003г.)

9. Вычислите 4ctg a, если cos a = 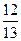и .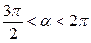

А) -3,6.

В) 9,6.

С) 0.

D) -9,6.

Е) 1,6.

(Вариант-24 №28 2003г.)

Коды правильных ответов

D	A	D	E	B	A	B	C	D

Тригонометрия – один из важнейших разделов математики. Чтобы успешно решать тригонометрические уравнения, упрощать тригонометрические выражения, нужно знать основные формулы тригонометрии и значения синуса, косинуса, тангенса, котангенса табличных углов. В одном из журналов «Математика» указан необычный способ, который можно применить для запоминания значений синусов и косинусов табличных углов. Это, конечно, мнемоническое правило, но в трудную минуту, например, на ЕНТ, оно может помочь.

Оказывается, значения синусов и косинусов углов «находятся» на нашей ладони. Рассмотрим правило нахождения синусов:

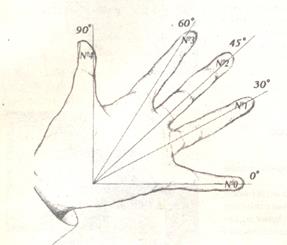
На пересечении продолжений мизинца и большого пальца находится бугор Луны. Измерим углы между пальцами (пальцы развести как можно сильнее). Угол между мизинцем и безымянным пальцем - 30º, угол между мизинцем и средним пальцем - 45º,угол между мизинцем и указательным пальцем - 60º, угол между мизинцем и большим пальцем - 90º. И это у всех людей без исключения. Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить пальцы с мизинцем, угол между лучами будет 0º, т.е. можно считать, что направление мизинца соответствует началу отсчета углов, т.е. 0º. Введем нумерацию пальцев:

Мизинец – №0 соответствует 0º;

Безымянный - №1 соответствует 30º;

Средний - №2 соответствует 45º;

Указательный - №3 соответствует 60º;

Большой - №4 соответствует 90º.

Нужно запомнить формулу: - половина квадратного корня из номера (n) пальца.

Номер пальца	Угол	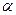Значение синуса
	0º	sin0º =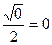
	30º	sin30º =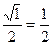
	45º	sin45º =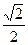
	60º	sin60º =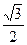
	90º	sin90º =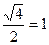

а и большого пальца находится бугор Луны.

Для определения косинуса угла пальцы пронумеровать с большого, а начало отсчета углов оставить по-прежнему от мизинца.

При решении тригонометрических уравнений и неравенств видаsin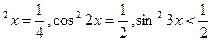 , чтобы получить ответ, данный в тестах, нужно решать, используя формулы понижения степени:

Например:

Решите уравнение: sin .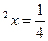

I cпособ решения:

sin ,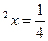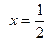

sin ; sin ;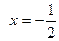

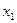= (-1)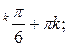 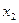= (-1)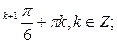

Объединяя решения, получаем ответ, данный в тестах: х =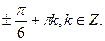

Но если использовать формулу 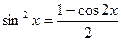, то получим сразу данный ответ. Этот способ решения для учащихся проще, т.к. нахождение объединения решений вызывает у них затруднения.

II cпособ решения:

sin 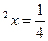, , 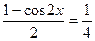, , 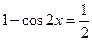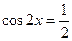2x =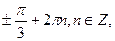

x =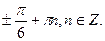

Аналогичный способ решения можно применить в следующих заданиях:

1. Решите уравнение: sin .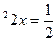

Решение:

, , , , , , .

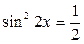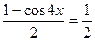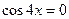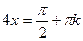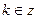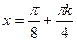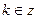А)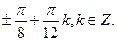

В)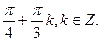

С)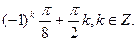

D)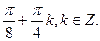

Е)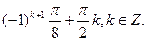

(Вариант-35 №25 2005г.)

2. Решите уравнение: cos .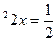

А) .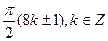

В) .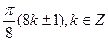

С) .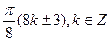

D) .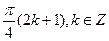

Е) .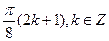

(Вариант-16 №30 2005г.)

3. Решите уравнение: sin 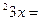3cos .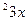

А) .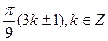

В) .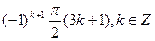

С) .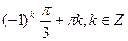

D) .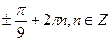

Е) .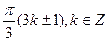

(Вариант-2 №5 2004г.)

4. Решите уравнение: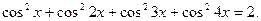

А) .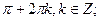

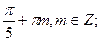
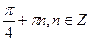В) .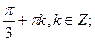

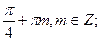
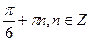С) .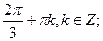

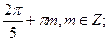
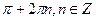D) .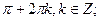

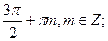
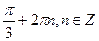Е) .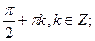

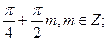
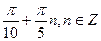(Вариант-5 №5 2004г.)

5. Решите неравенство: 3 – 4 соs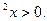

А) ( .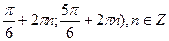

В) ( .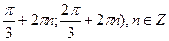

С) ( .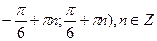

D) ( .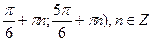

Е) ( .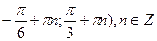

(Вариант-7 №9 2004г.)

(Вариант-35 №8 2004г.)

Коды правильных ответов

D	E	A	E	D

При решении тригонометрических уравнений, неравенств, упрощении тригонометрических выражений можно использовать правило:

Увидел сумму – преобразуй в произведение.