II. Свойства квадратного уравнения. Метод переброски. Применение теоремы Виета и обратной ей теоремы.

Большое значение имеет умение учащихся быстро находить корни приведенного квадратного уравнения по теореме, обратной теореме Виета.

Сложнее определить корни полного квадратного уравнения. При решении таких уравнений можно использовать метод «переброски», позволяющих свести задачу к нахождению целых корней вспомогательного уравнения. Этот метод состоит в следующем.

Пусть требуется решить квадратное уравнение .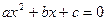

Для него , .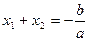

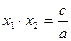Умножив обе части данного уравнения на а, перепишем его в виде .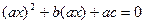

Введем замену у = ах, тогда в полученном уравнении , , .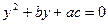

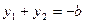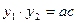Для решения исходного уравнения, 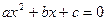достаточно решить вспомогательное уравнение 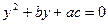. И его корни разделить на а.

Например:

1. Решите уравнение 6 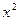+ х – 15 = 0.

Решение:

Запишем вспомогательное уравнение 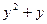- 90 = 0. Его корни .

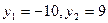Следовательно, исходное уравнение имеет корни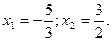

2. Решите уравнение 12 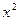+ 13х + 3 = 0.

Решение:

Запишем вспомогательное уравнение 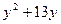+ 36 = 0. Его корни .

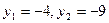Следовательно, исходное уравнение имеет корни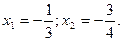

В дальнейшем, по мере накопления учащимся опыта в применении указанного приема можно не записывать вспомогательное уравнение, а проводить «мысленные» рассуждения: «Чтобы решить уравнение 3 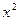- 11х + 6 = 0, надо подобрать два числа, сумма которых 11, произведение 18. Это 2 и 9. Следовательно, корни данного уравнения 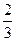и 3»

Этот прием можно использовать и при решении квадратных неравенств, разложении квадратного трехчлена на множители, при нахождении области определения функции, при решении уравнений, сводящимся к квадратным, в решении тригонометрических и логарифмических уравнений.

Например:

1. Разложите квадратный трехчлен на множители: 2 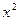+ 7х – 4.

Решение:

2х² + 7х -4 = 0 Запишем вспомогательное уравнение у² +7у -8 = 0. Его корни у₁=-8, у₂ = 1. Исходное уравнение имеет корни х₁ = -4, х₂ =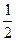

Ответ : 2х² +7х – 4 = 2(х+4)(х- )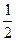

А) 2(х – 2) (х + 3).

В) 2(х – 1/2) (х + 4).

С) -2(х – 1/2) (х + 1/3).

D) -2(х + 3) (х + 4).

E) 2(х + 0,5) (х - 4).

(Вариант-4 №2 2003г.)

2. Решите неравенство: 5 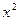+ 9х – 2 < 0.

A) .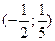

B)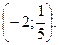

C)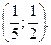

D) (-2; 0).

E)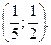

(Вариант-35 №7 2004г.)

3. Решите неравенство: 2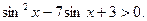

А)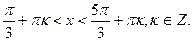

В) Нет решений.

С)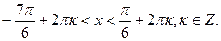

D)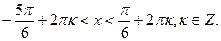

Е)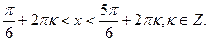

(Вариант-22 №3 2005г.)

4. Решите неравенство: 4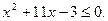

А)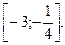

В)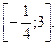

С)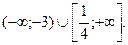

D)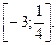

Е)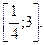

(Вариант-30 №15 2005г.)

5. Решите систему неравенств: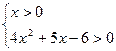

А) (2; 5).

В) (-3; 1,5).

С) (-1; 0,25).

D) (1; -3).

Е) (0,75; + ).

(Вариант-25 №20 2007г.)

6. Решите систему неравенств: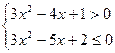

A) Нет решений.

B)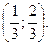

C)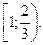

D)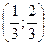

E)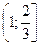

(Вариант-10 №22 2007г.)

7. Сколько целых решений имеет неравенство 1 - 5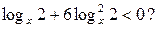

А) .

В) 4.

С) 1.

D) 3.

E) 2.

(Вариант-27 №14 2002г.)

8. Решите неравенство: 2 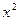-7х – 49 > 0.

A) .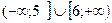

B)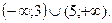

C)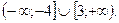

D)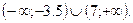

E)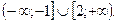

(Вариант-32 №13 2002г.)

9. Решите систему неравенств: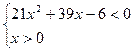

А) .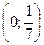

В) (4; -2).

С) (-2; -1).

D) (6; -3).

E) .

(Вариант-34 №20 2006г.)

10. Решите неравенство: 5 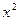+ 9х – 2 < 0.

А) .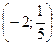

В) .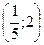

С) .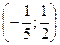

D) (-2; 5).

E) .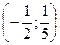

(Вариант-23 №8 2006г.)

Коды правильных ответов

B	B	C	D	E	A	D	D	A	A

Использование свойств квадратного уравнения 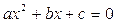дает значительные преимущества для быстрого получения ответа при решении некоторых квадратных уравнений.

1. Если в квадратном уравнении 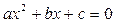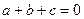, то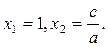

Доказательство:

По условию , .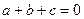

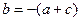Подставляем в уравнение .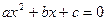

Получаем:

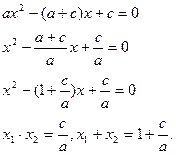
Следовательно: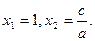

2. Если в квадратном уравнении 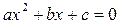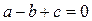, то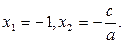

Например:

Решите уравнение .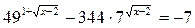

.

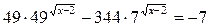
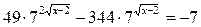Введем новую переменную: 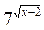= t.

.

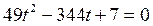Полученное уравнение очень сложно решить «обычным» способом. Если применить метод «переброски», то получим: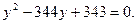

В полученном уравнении сумма коэффициентов 1 – 344 + 343 = 0.

Следовательно,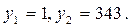

Корни исходного уравнения: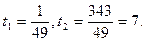

Возвращаясь к прежней переменной, получим:

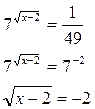
нет решений.

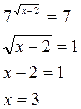
Ответ: х = 3.

Примеры:

А)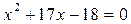

a + b + c = 0,

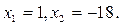
Б)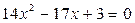

a + b + c = 0,

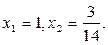
Эти свойства можно применить при решении уравнений:

1. Найдите самое наименьшее целое решение неравенства:

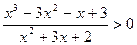
Указание:

В квадратном трёхчлене, стоящем в знаменателе дроби х² +3х +2, сумма коэффициентов а-в+с=0, следовательно х₁=-1, х₂=-2. Получаем: х² +3х + 2 =(х+1)(х+2).

A) 1.

B) 2.

C) -2.

D) -1.

E) 0.

(Вариант-9 №10 2004г.)

2. Решите уравнение: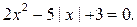

A) .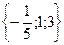

B) .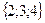

C) .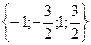

D) .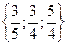

E) .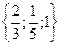

(Вариант-15 №4 2004г.)

3. Решите уравнение: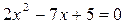

A) 2; 5.

B) -3; 3.

C) 2; 6.

D) 1,5; 4.

E) 2,5; 1.

(Вариант-9 №5 2002г.)

4. Решите неравенство: -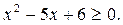

A) [-3; 2].

B) (- .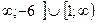

C) [2; 3].

D) [-6; 1].

E) (- .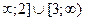

(Вариант-13 №15 2002г.)

5. Решите неравенство: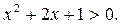

A) x > 0.

B) x = -1.

C) для любых х.

D) x < -1.

E) x .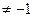

(Вариант-15 №15 2002г.)

6. Решите уравнение: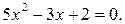

A) 0,6.

B) 0.

C) -0,6.

D) 1.

E) Корней нет.

(Вариант-16 №3 2005г.)

7. Решите уравнение: -3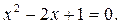

A) {-3; 3}.

B) {- .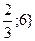

C) .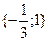

D) .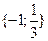

E) .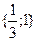

(Вариант-3, №6 2005г.)

8. Решите систему неравенств: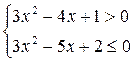

A) .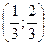

B) .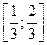

C) нет решений.

D) .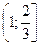

E) .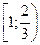

(Вариант-21 №16 2004г.)

9. Решите уравнение: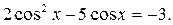

A) .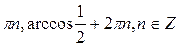

B) .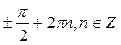

C) .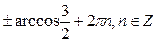

D) .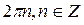

E) .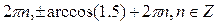

(Вариант-30 №6 2004г.)

10. Решите уравнение: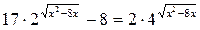

A) -1; 9.

B) 1.

C) 9.

D) -1.

E) -9; 1.

(Вариант-5 №12 2002г.)

Коды правильных ответов

E	C	E	D	E	E	D	C	D	A

При решении задач, связанных с теоремой Виета, либо теоремой, обратной теореме Виета, полезно использовать соотношения:

1.

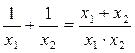
2.

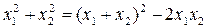
3.

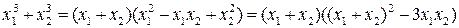
Эти соотношения можно использовать при решении следующих заданий:

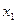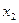1. Не вычисляя корней и уравнения 2 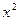+ 5х – 3 = 0, найдите: .

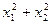Решение:

2х²+5х-3=0, перейдём к приведённому квадратному уравнению х²+2,5х-1.5=0, х₁+х₂=-2,5, х₁х₂=-1.5. Используя соотношение х₁²+х₂²=(х₁+х₂)²-2х₁х_2, получаем х₁²+х₂²=(-2,5)²-2·(-1,5)=6.25+3=9,25.

А) 10.

В) 9,25.

С) -5,7.

D) 25.

Е) 5.

(Вариант-6 №16 2007г.)

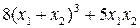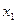2. Вычислить , где и 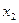- корни уравнения 9 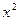+12х +2 = 0.

А) .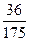

В) .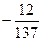

С) .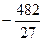

D) .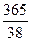

Е) .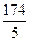

(Вариант-5 №17 2007г.)

3. Вычислите 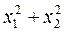, есл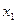и и 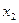различные решения уравнения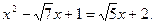

А) 14 + .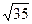

В) .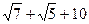

С) 14 + .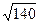

D) 14 +.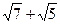

Е) 10 + 2 .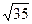

(Вариант-27 №4 2004г.)

(№593, 2006г. Тестовые задания, Кокшетау)

4. Найдите сумму квадратов корней уравнения 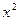+ 3х – 15 = 0.

Ответ: = ( .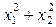

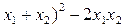(№617 2006г. Тестовые задания, Кокшетау)

5. Найдите сумму квадратов корней уравнения 3 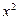- 5х – 2 = 0.

Ответ: = .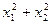

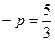(№618, 2006г. Тестовые задания, Кокшетау)

Коды правильных ответов

B	C	C		5/3