Оценка переменных параметров

Рассмотрим теперь многошаговый процесс получения данных на­блюдения и принятия решений, к которому сводятся многие практические задачи, в частности, задачи фильтрации.

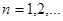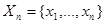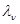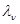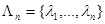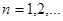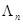Пусть для любого n-го шага ( ) совокупность данных наблюдения описывается вектором , каждая компонен­та которого зависит от параметра . Значения меняются от шага к шагу, а их совокупность для n-го шага описывается вектором увеличивающейся размерности. Задача статистического решения заключается в том, чтобы на каждом n-м шаге ( ) с помощью оценить значение . Последовательность этих оценок для каждого фиксированного значения п дает оценку вектора 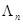в целом, причем каждая его компонента 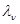( ) оценивается с соблю­дением принципа физической реализуемости, то есть зависит только от тех данных наблюдения, которые получены до -ro шага включительно. При этом, как всегда, и 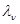, вообще говоря, являются векторами той или иной (одинаковой или разной) размерности.

В практических приложениях индекс чаще всего соответствует дискретному времени, a 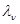- значению некоторой функции 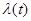в момент времени 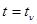. При этом полученная оценка является оценкой функции 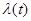в дискретных точках. При переходе к непрерывному времени век­тор переходит в отрезок реализации наблюдаемого процесса 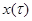на интервале времени от 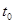до 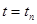, вектор 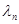- в отрезок реализации процесса 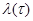на том же интервале, а задача статистического решения заключается в том, чтобы на основании наблюдения 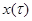на интервале 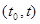оценить значение 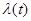для каждого момента времени t, большего 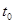и меньшего некоторого 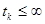, соответствующего прекращению про­цесса оценивания.

Пусть последовательность 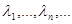обладает марковским свойством, то есть для любого п

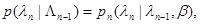(10.4.1)

где 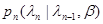- переходная плотность вероятности, зависящая от совокупности неизвестных параметров 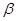, описывающих априорную неопределенность статистических свойств последовательности 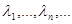Выбором соответствующей размерности вектора 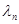и подхо­дящей совокупности параметров 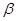практически всегда можно добиться того, что соотношение (10.4.1) выполняется. Будем считать также, что условное математическое ожидание

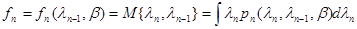(10.4.2)

и условная корреляционная матрица

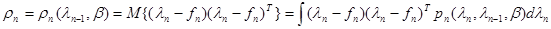(10.4.3)

существуют, причем функция 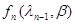дифференцируема по 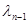и 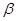. Важным частным случаем, для которого выполняются условия (10.4.1) – (10.4.3), являются процессы, описываемые рекуррентным соот­ношением

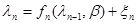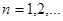, (10.4.4)

где 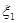, ,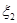… - последовательность независимых векторных случайных величин с корреляционной матрицей

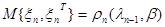, (10.4.5)

Отметим, что последняя может быть вырожденной и может содержать нулевые диагональные элементы, что соответствует несобственному условному распределению вероятности вектора 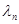, целиком сосредото­ченному на некоторых гиперповерхностях пространства, в котором задан этот вектор. Наряду с (10.4.4) часто также используется соотношение

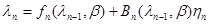. (10.4.6)

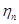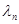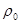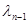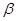где - случайный вектор, размерность которого не обязательно сов­падает с размерностью , имеющий корреляционную матрицу , не зависящую от и , а 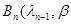- прямоугольная матрица соот­ветствующих размеров. В этом случае

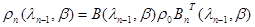. (10.4.7)

При переходе к непрерывному времени аналогом рекуррентного соотношения (10.4.4) является стохастическое дифференциальное урав­нение

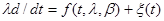, (10.4.8)

где 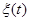- дельта-коррелированный процесс («белый» шум) с корре­ляционной функцией

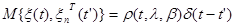. (10.4.9)

При дискретизации этого уравнения мы, очевидно, возвращаемся к рекуррентному соотношению (10.4.4), в котором при достаточно малых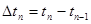

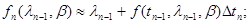
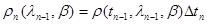, (10.4.10)

а условная плотность вероятности (10.4.1) является гауссовой.

Будем считать также, что наряду с неопределенностью статистиче­ского описания переменного параметра 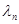, подлежащего оценке, существует априорная неопределенность в отношении данных наблю­дения, которая приводит к заданию распределения вероятности величин с точностью до совокупности неизвестных параметров 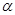, то есть для любого

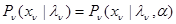. (10.4.11)

Набор плотностей вероятности (10.4.1) и (10.4.11) для дает параметрически неопределенное статистическое описание задачи. В соответствии с общими результатами гл. 6 адаптивное байесово правило решения интересующей нас задачи заключается в формирова­нии совместной оценки величин 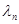, 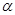и 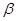. Для того чтобы добиться единообразия в формулировке этой задачи совместной оценки, припи­шем параметрам 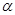и 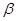также индекс «n», формально рассматривая их как меняющиеся от шага к шагу. Чтобы при этом не исказить существа дела, связанного с их фактической неизменностью, необходимо считать, что их последовательные значения 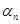, 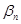и , 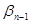связаны между собой соотношениями

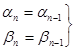. (10.4.12)

С учетом (10.4.12) мы, очевидно, имеем право записать

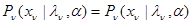(10.4.13)

и

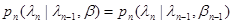, (10.4.14)

поскольку в силу (10.4.12) безразлично, какой индекс приписать 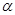и 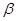. Очевидно, также, что выражения (10.4.12) являются частным слу­чаем рекуррентного соотношения (10.4.4) и им можно поставить в соот­ветствие переходные плотности вероятности

;

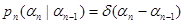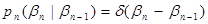. (10.4.15)

Объединим теперь параметры 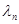, , 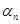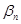в единую совокупность, введя вектор

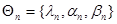. (10.4.16)

суммарной размерности. Последовательность 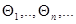, очевидно, удовлетворяет марковскому свойству и имеет переходную плотность вероятности

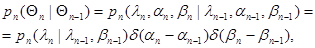(10.4.17)

причем, условное математическое ожидание и условная корреляционная матрица 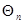, соответственно равны

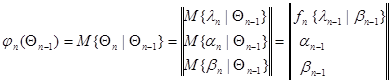, (10.4.18)

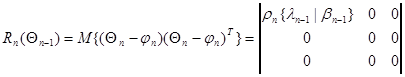. (10.4.19)

Аналогично плотность распределения вероятности для наблюдаемо­го значения (10.4.13) можно записать:

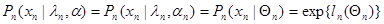, (10.4.20)

имея в виду, что она зависит от части из совокупности параметров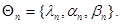

С помощью этих нехитрых операций так же, как в случае задачи оценки постоянных параметров, мы добились полного устранения фор­мальных различий между интересующими нас полезными параметрами 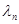и «мешающими» параметрам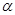и и 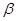, описывающими априорную неопределенность. По форме задача свелась к байесовой оценке век­тора 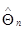с переходной плотностью вероятности (10.4.17) по совокупности наблюдаемых данных 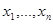, каждое из которых имеет распределе­ние вероятности с плотностью (10.4.20). Решение этой задачи хорошо известно и в асимптотическом гауссовом приближении для апостериорной плотности вероятности 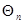задается следующей системой рекуррентных соотношений, обеспечивающих последовательное вычисле­ние оценочных значений 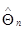параметра 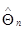и апостериорной корреляци­онной матрицы 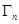, характеризующей ошибки оценивания:

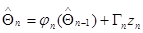, (10.4.21)

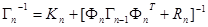, (10.4.22)

где

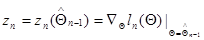; (10.4.23)

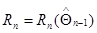; (10.4.24)

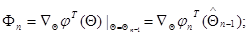(10.4.25)

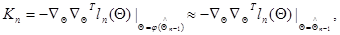(10.4.26)

а функции 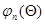, , 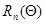определяются выражениями (10.4.18) - (10.4.20) соответственно.

Рекуррентные соотношения (10.4.21), (10.4.22) являются обобще­нием рекуррентных соотношений гл. 7 для оценок максимального правдоподобия постоянных параметров. Как и в гл. 7, при вычислении весовой матрицы

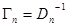(10.4.27)

практически без ухудшения точности оценки параметра 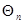можно заменить в соотношении (10.4.22) матрицу матрицей

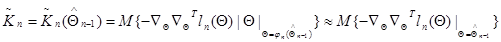, (10.4.28)

получающуюся подстановкой значения 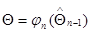или 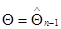в мат­рицу 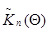, определенную выражением

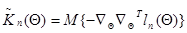. (10.4.29)

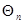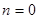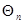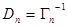Выбор начальных условий для рекуррентных соотношений (10.4.21), (10.4.22) осуществляется так же, как для рекуррентных соотношений гл. 7 с учетом ограниченных сведений об априорном разбросе значений при , если последние имеются, и нулевыми для и при 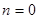, если всякая информация о начальных значениях отсутствует. Как и в случае постоянных параметров, если только начиная с некото­рого п матрица 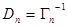становится невырожденной и существует обратная ей матрица 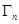, то есть действительно имеется возможность изме­рения всех компонент параметра 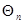, то начальные условия быстро забы­ваются и очень слабо влияют на значения оценок 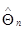и характеристики их точности. В связи с этим при полном отсутствии априорных сведений для начальных значений можно задавать матрицу 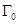любым подходящим способом, обеспечивающим обращение матриц в (10.4.22) на начальных шагах, с соблюдением единственного условия, чтобы собственные числа матрицы 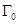, которые характеризуют априорный разброс начальных значений 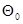, были достаточно большими.

Для улучшения скорости сходимости рекуррентной процедуры и уменьшения влияния произвола в выборе начальных условий полезно более точно вычислить апостериорную плотность вероятности на на­чальных шагах для некоторого 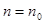, не прибегая к гауссовой аппро­ксимации, и затем найти то значение 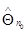, которое обращает её в максимум.

Это максимизирующее значение 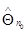вместе с матрицей вторых про­изводных логарифма апостериорной плотности вероятности в точке 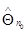и являются наилучшими начальными значениями для рекуррент­ной процедуры, которая начинается с 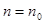. Как правило, указанная максимизация требует решения трансцендентных уравнений, поэтому число начальных шагов следует выбирать исходя из компромисса меж­ду сложностью этих уравнений и желанием получить наиболее точное начальное приближение. Практически целесообразно выбирать 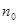равным тому минимальному значению, для которого все компоненты максимизирующего значения 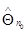являются нетривиальными оценками вектора 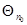, то есть действительно зависят от полученных за 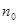шагов данных наблюдения.

Если далее в процессе выполнения рекуррентной процедуры матрица 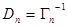не становится особенной, то заданная система полезных пара­метров 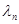и параметров 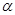и 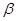, выбранных для описания априорной неопределенности, является допустимой в том смысле, что все эти параметры действительно могут быть оценены по имеющимся данным наблюдения. Если же матрица вырождается, то необходимо либо исключить часть этих параметров из числа оцениваемых, приписав им те или иные выбираемые на основе априорных предположений фиксированные значения (результат оценки остальных параметров будет за­висеть оттого, сколь точно эти значения соответствуют действительным), либо расширить объем данных наблюдения, так, чтобы обеспечить воз­можность оценки всех имеющихся параметров.

С точки зрения практического использования, благодаря широкому распространению ЭВМ, наибольшую ценность имеют именно рекуррент­ные соотношения (10.4.21), (10.4.22), которые позволяют решить гро­мадное количество самых разнообразных прикладных задач. Однако для аналитического исследования более удобны дифференциальные уравнения, которые получаются из рекуррентных соотношений (10.4.21), (10.4.22) соответствующим предельным переходом либо могут быть найдены непосредственно при рассмотрении процессов с непрерывным временем. При этом соответствующие стохастические дифференциаль­ные уравнения для оценок, как и исходные уравнения для оцениваемых параметров, могут пониматься либо в смысле Ито, либо в смысле Стратоновича с теми особенностями в построении схем устройств, моделиру­ющих эти уравнения, которые следуют из различия в этом понимании. Дополняя уравнение (10.4.8) дифференциальными уравнениями для параметров 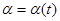и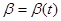

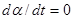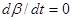, , (10.4.30)

получаем дифференциальное уравнение для составного вектора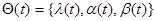

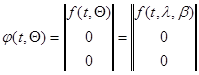; (10.4.31)

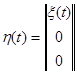(104.33)

- дельта-коррелированный случайный процесс с корреляционной мат­рицей

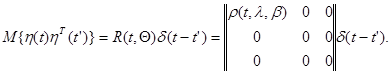(10.4.34)

Соответствующие дифференциальные уравнения для оценки 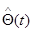и апостериорной корреляционной матрицы 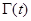имеют вид

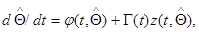(10.4.35)

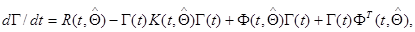(10.4.36)

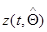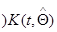где и определяются так же, как в гл. 7 формулами (7.5.43) и (7.5.47) с возможной заменой 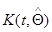на 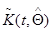из (7.5.49), а матрица 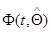определяется соотношением

.

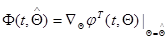Дифференциальное уравнение для матрицы

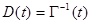(10.4.37)

имеет вид

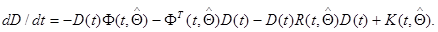(10.4.38)

Матрица 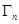, определяемая соотношением (10.4.22), и соответствен­но 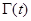,определяемая дифференциальным уравнением (10.4.36), пред­ставляют собой апостериорные корреляционные матрицы оцениваемой совокупности параметров. Корреляционная матрица ошибок оценивания этих параметров

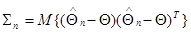(10.4.39)

и соответственно

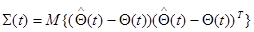(10.4.40)

асимптотически (при достаточно большом объеме данных наблюдения или при достаточно высокой точности единичных измерений параметров 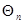по одному наблюдению ) определяются теми же рекуррентными соотношениями и дифференциальными уравнениями, что 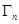и 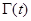, если в них всюду заменить оценочные значения параметров 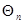их истинными значениями, а матрицы 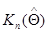и 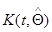их математически­ми ожиданиям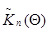и и 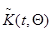соответственно. Этот факт достаточно хорошо известен для неадаптивного случая, а в силу того, что при наличии априорной неопределенности задача оценки сводится к обычной байесовой задаче относительно расширенной совокупности параметров, полностью переносится и на адаптивный случай. Указанное совпадение полностью аналогично асимптотической сходимости корре­ляционной матрицы ошибок оценивания постоянных параметров к ма­трице, обратной информационной матрице Фишера. Таким образом, при­веденные выше рекуррентное соотношение (10.4.22) и дифференциальное уравнение (10.4.36) дают возможность простой подстановкой в них истинных значений оцениваемых параметров найти точность оценки этих параметров.

Так же, как в §10.2, дискретный (10.4.21), (10.4.22) и непрерывный (10.4.35), (10.4.36) алгоритмы формирования оценок автоматически учи­тывают наличие данных обучения, описание которых производится со­ответствующим заданием функций правдоподобия 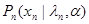(и соот­ветственно 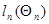или 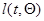), где под понимается вся совокупность наблюдаемых на n-м шаге данных, возможно (при наблюдении на интервале обучения «чистых» реализаций значений измеряемого пара­метра) включающих в себя и значения 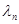.