Программный материал для группы детей шестого года жизни

Упражнять детей в понимании того, что множество может быть составлено из разных по качеству элементов; элементом множества может быть как отдельный предмет, так и целая

группа.

Упражнять детей в выделении нескольких частей множеств по тому или иному признаку, устанавливать отношения между конечным множеством и его частями: целое больше своей части; устанавливать между одинаковыми по численности частями взаимно-однозначное соответствие, определять большую, меньшую часть или их равномощность и вновь воссоединять эти части в единое целое, познакомив с операцией объединения множеств.

Познакомить с операцией удаления части множества.

Познакомить со значением слова один (одна, одно), которое обозначает не только один предмет, но и целую группу предметов как одну часть множества.

Количество и счет. Учить детей считать в пределах 10. Закреплять и формировать умения и навыки отсчитывания предметов в пределах 10 по образцу и заданному числу. Уметь определять равное количество в группах разных предметов, правиль-

но обобщать множества числом на основе счета и сравнения множеств (здесь всех предметов по 5, по 8, по 10).

Уметь считать предметы при разном пространственном их расположении (а не только при линейном).

Уточнить представление, что число не зависит от характера элементов, их качественных признаков (от величины предметов, от расстояния между ними, от пространственного расположения), а также от направления счета (слева — направо, справа — налево, с середины в стороны и др.).

Знать количественный состав числа из единиц в пределах пяти (пять — это один, еще один, еще один, еще один и еще один) на конкретном материале.

Учить сравнивать смежные числа в пределах 10, опираясь на сравнение конкретных множеств; знать, как из неравенства сделать равенство (восемь больше семи; если к семи добавить один, будет по восемь, поровну; семь меньше восьми, в множестве семь не хватает одного, значит, если из восьми вычесть один, то будет в обеих группах по семь, поровну).

Учить детей порядковому счету в пределах 10; уметь различать значение вопросов «какой», «который», «сколько» и правильно отвечать на них.

Начать формировать понятие, что предмет можно разделить на несколько равных частей (на две, четыре). Например, одно яблоко можно разделить пополам, т. е. на две равные части, каждая из частей называется одной половинкой; яблоко можно разделить на четыре равные части, каждая из частей называется одной четвертью яблока. Точно так же можно разделить квадрат, круг на несколько равных частей и получить половину квадрата, одну четверть квадрата и т. д. (дети сами делят яблоко, круги др.).

Величина. Уточнять представления об изменениях протяженности предметов по длине, ширине, высоте, толщине, приучая детей правильно отражать эти умения в речи («Стало длиннее», «Это тоньше», «Веревка толще нитки» и т. д.).

Развивать глазомер детей, учить на глаз определять длину или толщину палки, ширину ленты, высоту забора, дерева, оценивая воспринимаемые размеры путем сопоставления с длиной известных ребенку предметов или отрезков (толщиной с палец, высотой с человека, тонкая, как нитка, толстая, как веревка, длиной в два шага и др.).

Форма. Закреплять представления о шаре, кубе, цилиндре, конусе, брусе (прямоугольный параллелепипед), квадрате, прямоугольнике, треугольнике, круге, овале, трапеции и правильно называть их.

Учить считать количество вершин, сторон, углов в разных плоских фигурах.

Познакомить с различием некоторых геометрических фигур (прямоугольника и трапеции, конуса и пирамиды).

Учить видеть геометрическую форму в жизненных предметах: что похоже на шар (мячик, арбуз и др.), на цилиндр (стакан, банка и др.), на конус (воронка, пирамидка и др.), на круг (блюдце, тарелка и др.), на прямоугольник (крышка стола, стена, пол, потолок, дверь и др.). на квадрат (платочек), на треугольник (косынка), на овал (очертания продольного разреза яйца, край блюда и др.), на трапецию (детский стол, крыша домов и др.).

Ориентировка в пространстве. Закреплять умения определять словом положение того или иного предмета по отношению к себе (впереди меня идет Андрюша, слева от меня стол); по отношению к другому (справа от куклы сидит заяц, а впереди куклы стоит петух).

Упражнять в пространственной ориентировке во время движения, учить изменять направление движения во время ходьбы, бега, гимнастических упражнений.

Упражнять в определении своего положения среди окружающих предметов (например, я стою за стулом, я стою около стула, я стою среди кубиков, я стою перед Мишей, напротив Миши, сзади Миши, справа от Лены и слева от Коли. Значит, Коля от меня справа, а Лена от меня слева и т. д.).

Ориентировка во времени. Научить последовательно называть дни недели. Определять, какой день сегодня, какой был вчера и какой будет завтра.

Развивать у детей «чувство времени» — знакомя практически с длительностью отдельных временных отрезков, учить определять, что можно сделать за какой-либо из этих отрезков.

Ориентировка в весе. Развивать у детей барическое чувство («чувство веса»), находить равные и неравные по весу предметы, взвешивая их па ладонях, сначала на контрастных показателях. Определять по весу предметы, раскладывая их в восходящем или убывающем порядке.

Примерные занятия: множество, число и счет

Ознакомление с множеством.

В предшествующих группах дети много раз практически имели дело с множествами. Они знакомы с тем, что всякие конкретные совокупности состоят из отдельных предметов, но можно в этих совокупностях (множествах) выделить и отдельные части, обладающие теми или иными признаками.

Перед воспитателем старшей группы стоит задача —углубить представления детей о множестве, раскрыть значение терминов множество, элементы множества и приучить пользоваться ими.

Воспитательница предлагает детям привести примеры множеств. «Множество квадратов», «Множество дверей в комнате», «Множество домов на улице»,— называют дети. Воспитательница

стучит несколько раз по столу и спрашивает: «А как можно назвать это?» — «Множество звуков», «Множество движений»,— отвечают дети. Воспитательница предлагает подумать, из чего составляется всякое множество. Дети отвечают, что множество составляется из отдельных предметов, отдельных звуков, отдельных движений. Воспитательница, обобщая, говорит, что эти отдельные предметы, отдельные звуки, отдельные движения, входящие в состав множества, называются элементами множеств. Она называет несколько множеств и просит сказать, что в том или другом случае будет именоваться множеством и его элементом (множество карандашей, множество детей, множество столов в группе, множество игрушек и др.).

Далее с помощью воспитателя дети обнаруживают, что не все элементы в множествах бывают однородными, например элементами множества «мебель» будут: столы, стулья, шкаф, полка, буфет и другое, т. е. одни элементы одинаковые, как столы, стулья, а другие разные, как полка, буфет шкаф. «Что же можно сказать об элементах множества?» — спрашивает воспитательница, подводя детей к обобщению: множество может состоять из элементов разного качества. Она предлагает самим детям составить какое-либо множество из элементов разного качества. Дети приносят игрушечных мишку, петуха, лошадку. «Как можно назвать это множество?» — ставит новый вопрос воспитательница. Одни дети говорят, что это множество игрушек, а другие — что это множество животных. Оба ответа верны.

Затем воспитательница сама ставит множество из кубиков на стол, а другое, из петушков, на стул и спрашивает: «Что можно сказать про эти множества?» Дети говорят, что одно множество из кубиков, кубики — это элементы множества, а другое множество из петушков, петушки — это элементы множества петушков. «Можно ли объединить оба множества? Как тогда будет называться это множество?» — «Множество предметов», «Множество игрушек»,— отвечают дети. «Когда мы объединили эти два множества, что можно сказать про каждое из них?» —■ «Каждое из них будет частью всего множества»,— слышны ответы детей. По просьбе воспитателя дети уточняют, что в множестве игрушек две части, и называют, из чего состоит каждая часть. Далее детям предлагается сравнить эти части, определить, какая же из них по численности больше (меньше) или они равны, и сказать, что больше: все множество или какая-либо часть его.

Так воспитательница подводит детей к пониманию, что несколько отдельных частей могут быть объединены в одно целое множество, что (конечное) множество «больше» своей части. Здесь нет еще арифметического действия сложения, но в подобных упражнениях закладывается его математическая основа. На первом занятии воспитательница показывает два-три вида различных мелких игрушек, например группу уток, группу гусей,

группу кур, и спрашивает, можно ли все эти группы объединить в одну и как тогда будет называться вся группа в целом и каждая из них. Дети задумываются, затем соглашаются объединить все группы, указывают, что это будет множество игрушек. «А как иначе можно назвать такое множество (эти объединенные группы)?»—стимулирует мысль детей воспитательница. «Это будет множество птиц»,— говорит один из детей. «А назовите части в этом множестве птиц».—«Одна часть —утки, одна часть — гуси, одна часть — куры»,—отвечают дети. «Сколько же частей в этом множестве птиц?» — ставит новый вопрос воспитательница. Дети отвечают.

На другом занятии детям предлагается самим создать множество из разных частей, например, дети берут две группы деревьев — березы, елки. Объединяя их, дети говорят, что они составили одно множество деревьев из двух частей: одна часть — березы и одна часть — елки и т. д. Воспитательница направляет внимание детей на отношения между частью и целым: «Чего же больше — всех деревьев вместе или только одних берез?» и т. д.

В качестве материала на подобных занятиях могут быть использованы различные предметные картинки, например кастрюли, тазы, поварешки — множество, называемое кухонной посудой; чашки, кружки, чайники, кофейники, молочники, тарелочки— множество, называемое чайной посудой, и т. д.

Такие занимательные занятия позволяют детям упражняться в различной группировке (приемах классификации), которая, в свою очередь, подводит к пониманию как родовых, так и видовых понятий, а также к более глубокому усвоению множества, в частности отношений между частью и целым.

Составляя объединенные множества, дети считают в них количество частей и количество отдельных элементов, входящих в состав части. Допустим, дети из трех групп животных (собак, кошек, лошадок) составили объединенное множество домашних животных. Считая количество этих групп, они называют: одна, две, три, всего три части. Определяя, какая из частей больше, меньше или они равны по численности, дети считают элементы в этих частях; допустим, считая собак, выясняют, что их три (одна, дзе, три), а кошек — больше (одна, две, три, четыре), а лошадок— меньше (одна, две). Считая элементы в виде отдельных предметов и составные части единого множества, они пользуются теми же словами-числительными. На эту сторону важно обратить особое внимание детей, подчеркнув, что слово один служит количественным показателем не только отдельного предмета, но и целой группы, части, если нас интересует количество частей в множестве. Дети начинают понимать, что они могут считать как части множества, так и отдельные предметы внутри каждой части множества. Постепенно у детей будет разрушаться односторонняя связь слова один лишь с конкретной отдельностью, а это

значит, что они начнут осознавать значение числа один как показателя мощности множества.

Воспитательница предлагает детям самим перечислить отдельности или группы, которые можно назвать числом один. «Один большой мишка», «Одна группа мишек на полке», «Одна группа кукол сидит на диване, а одна кукла сидит за столом», «Один аквариум». «В аквариуме много рыб: одна часть-—маленькие рыбы и одна часть — большие рыбы», «Один конус и одна группа кубиков стоят на полке»,— говорят дети.

Упражняя детей в распознавании множеств и их элементов, воспитательница предлагает показать то или иное множество в целом и элементы множеств, составленных как из отдельных предметов, так и из отдельных частей.

Например, на столе стоит бокал с красными флажками. Дети говорят, что в бокале много красных флажков. «Имеются ли части в данном множестве?» — ставит вопрос воспитательница. Дети отвечают, что частей здесь пет. Воспитательница ставит в тот же бокал еще группу желтых флажков. Дети отвечают, что теперь в множестве флажков имеются две части — желтые и красные флажки. Воспитательница предлагает подумать, как можно, не считая, сказать, какое из подмножеств по численности больше. Дети вносят разные предложения: составить из красных и желтых флажков пары, разложить те и другие в ряд друг под другом, один под одним. Пользуясь тем или иным приемом, дети определяют, какая из сравниваемых частей больше какой, какая меньше какой (красных флажков больше, чем желтых, а желтых флажков меньше, чем красных).

Затем воспитательница предлагает самим детям составить множество из частей (кто как хочет). «Я взял сначала множество кружков и объединил их с множеством треугольников и множеством квадратов,— рассказывает один ребенок,— получилось множество разных фигур». Остальные дети также устанавливают количество частей своего множества. Но вот один ребенок сообщает: «Множество желтых кружков я объединил с множеством кружков красных и взял еще один зеленый кружок».— «А разве мы считали количество отдельных кружков? Ведь мы считали количество частей, которые объединили в одно множество». Ребенок задумывается. Воспитательница быстро развешивает несколько желтых кружков и предлагает Мише показать на доске, с какими кружками он объединил свое множество. Миша раскладывает несколько красных кружков и вешает еще один зеленый. «Сколько же отдельных частей ты объединил в одно множество кружков?» — «Три»,— отвечает Миша и показывает их. «Вот это правильно: зеленый кружок тоже отдельная часть, потому что он уже другого цвета, хотя зеленый кружок всего лишь один. Видите, дети, как Миша интересно составил множество из трех частей. Один кружок является

такой же частью большого множества кружков, как и другие»,— уточняет воспитательница.

Подобные занятия вызывают интерес у детей: они сами берут то или иное исходное множество, а затем объединяют его с другими множествами, отличающимися от основного какими-либо признаками. «Я множество ромашек объединил с множеством колокольчиков и маков. Я составил одно общее множество цветов из трех частей».— «А сколько отдельных цветов в каждой части?» — «В части из ромашек — пять, в части из колокольчиков— два, а в части маков — один».— «Сколько же всего частей в твоем множестве?» — «Три».— «А сколько отдельных цветков в твоем букете?» — «Всего восемь».— «А как называются отдельные предметы в множестве?» — «Это его элементы».— «Что же больше по-твоему: часть или все множество в целом?» — спрашивает воспитательница. «Часть меньше целого», — отвечает ребенок.

Дальше можно познакомить детей и с операцией удаления части множества. Сначала это целесообразно сделать на множестве, состоящем из трех частей. Воспитательница вешает на доске множество, состоящее из красных, желтых и зеленых кружков. Дети определяют количество частей данного -множества. Затем одну из частей она снимает. Дети говорят, что «множество уменьшилось»: остались только две части. Вызванный ребенок удаляет еще одну часть, множество снова уменьшается: теперь осталась лишь одна часть. Значит, если из основного множества удаляется часть его, множество уменьшается. Дети упражняются в этой операции: взяв одну часть белых грибов и объединив ее с одной частью сыроежек, они составляют единое множество грибов, а затем удаляют из него любую часть, после чего у них остается лишь одна (та или иная) часть. Операция удаления части из конечного множества послужит основой для усвоения детьми в дальнейшем арифметического действия вычитания.

Обучение

счету и отсчету

предметов.

Обучение счету и отсчету предметов продолжается в этой группе путем сравнения равных и неравных по численности множеств, выраженных смежными числами: пять и пять, пять и шесть, шесть и шесть, шесть и семь, семь и семь, семь и восемь, восемь и восемь, восемь и девять, девять и девять, девять и десять, десять и десять. Эти 11 случаев не следует растягивать на длительный период изучения. Сначала можно на од-ном-двух занятиях поупражнять детей в счете до семи, а затем перейти к счету в пределах девяти и, наконец, в пределах десяти. Ведь при счете в пределах десяти будут повторяться все промежуточные случаи. Задача же первых занятий состоит в том, чтобы показать на основе сравнения множеств, выраженных смежными числами, сам принцип образования следующего за числом п числа как п + 1, и любого предыдущего числа как п —

■—1, т. е. практически познакомить детей с принципом построения натуральной последовательности чисел.

Поэтому на подобных занятиях используются по-прежнему две полоски, на которых раскладываются равномощные или не-равномощные множества. Например, разложив на верхней и нижней полосках по семь кружков, Мара передвигает один из кружков с нижней полоски на верхнюю и говорит: «Теперь здесь больше — здесь восемь, а на нижней (считает) шесть».— «Сколько же надо добавить на нижнюю полоску, чтобы на ней стало столько же, сколько сейчас у тебя на верхней?» — «Семь и восемь»,— говорит девочка, имея в виду отсутствующие два кружка. «Что же, ты добавишь сразу семь кружков, а затем еще восемь?»— «Нет, что вы! Только два. Вот посмотрите: это — семь, а это — восемь».— «А сколько же всего у тебя на каждой полоске, когда ты добавила внизу два кружка?» — «По восемь кружков, поровну».

Ответ: «Добавить семь и восемь» — показывает, что у детей еще не отдифференцировалось понятие количественного значения числа от порядкового; называя количественные числительные семь и восемь, они придают им смысл порядковых, имея в виду, что надо прибавить седьмой и восьмой.

Воспитательница может предложить подумать, какое будет число, если к восьми кружкам добавим еще один кружок? Отвечая, ребенок должен обязательно практически проверить правильность своего ответа. Допустим, он прибавляет на верхней полоске один кружок, пересчитывает множество и убеждается, что ответ его был правильным. Затем он с левого конца ряда передвигает один кружок на нижнюю полоску, и на ней оказывается девять кружков, а на верхней остается восемь кружков.

Такие практические упражнения создают основу для понимания взаимно-обратных отношений. Эти знания могут закрепляться при проведении различных вариантов занятий, на которых предлагается сосчитать количество предъявленных предметов, а самим детям взять на один больше или на один меньше, разложив предметы друг под другом, чтобы сразу было видно, где больше, где меньше.

Воспроизведение множеств по устно названному числу.

На следующих занятиях дети сами отсчитывают из большего количества указанное им число предметов. «Миша принесет семь лодочек, а Ира — восемь петушков»,— дает задание воспитательница. Предварительно она объясняет детям, что они должны запомнить, кому сколько чего принести, а отсчитав, не забыть количество предметов. На вопрос воспитателя: «.Сколько же петушков ты принесла?» — Ира должна ответить без повторного счета: «Я принесла восемь петушков».

Можно предложить детям и такое задание, когда требуется запомнить количество предметов, их цвет и пространственное расположение. Например, воспитательница предлагает поло-

жить слева от себя шесть зеленых треугольников, а справа от себя четыре красных треугольника. Затем дети рассказывают, каких сколько и где лежат. «А что еще можно о них сказать, если ты не знаешь, где сколько?» — «Слева у меня множество зеленых треугольников, а справа множество красных треугольников».— «А нельзя ли эти множества объединить в одно? Что тогда можно сказать про это множество?» Дети объединяют обе группы треугольников и говорят, что у них одно множество треугольников. Но это множество состоит из двух частей: одна часть — зеленые треугольники, а другая часть — красные треугольники. Воспитательница предлагает припомнить, сколько треугольников входит в состав красных и сколько в состав зеленых.

Что должны сообразить дети, выполняя такое задание? То, что перед ними два множества, которые м о г yj быть объединены в одно, состоящее из двух частей, при этом каждая из них обладает своим цветом; а также помнить о связи количества с цветом треугольников и о месте расположения каждой из групп (справа или слева).

По мере упражнений все связи числа с предметом, его цветом, пространственным расположением предметов становятся привычными для детей, и количество ошибок при выполнении заданий постепенно уменьшается. В значительной степени этому помогает громкое проговаривание (самоотчет). Выполнение задания должно сопровождаться опросом нескольких детей. Надо учитывать, что детям не сразу удается рассказать, что они сделали, поэтому можно помочь наводящими вопросами, например: «Какого цвета и сколько треугольников у тебя лежит справа?», «А слева какого цвета треугольники и сколько их?» и т. д.

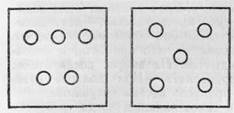
Рис. 14.

Обучение

счету при разном

пространственном

расположении

предметов.

в старшей группе вполне можно варьировать расположение предметов. Дети должны научиться считать предметы «по кругу», по вертикали, в виде числовой фигуры и расположенные неопределенной группой (рис. 14). Важно при этом обратить их внимание на то, что необходимо запомнить, с какого предмета они начали счет, чтобы не сосчитать дважды один и тот же предмет и в то же время не пропустить ни одного. Целесообразно поэтому постепенно усложнять пространственную форму расположения элементов множества, например, в виде вертикального ряда, по наклонной линии. Дети склонны принимать за точку отсчета тот предмет, который расположен ближе к ним. Можно предложить детям посчитать о г себя (снизу вверх и сверху вниз), доказав этим, что

результат будет один и тот же, потом также посчитать и по наклонной линии. При горизонтальном расположении целесообразно посчитать слева направо (как делали до сих пор), а также справа налево. Далее детям можно предложить посчитать количество кружков при разном расположении их в числовой фигуре. Показав различные способы сосчитывания, следует обсудить с детьми наиболее удобный из них. Воспитательница подчеркивает, что считать можно в любом направлении, лишь бы не пропустить какой-либо элемент множества.

Обучение

пониманию

значения числа

как показателя

определенного

класса множеств.

В старшей группе продолжается дальнейшее развитие понимания числа как показателя, отражающего определенный класс множеств. Этому могут способствовать различные приемы, используемые на занятиях. Например, воспитательница предлагает взять три-четыре вида различных предметов, но в равном количестве, показать это равенство практически, разложив предметы рядами друг под другом.

Аналогичное занятие может быть проведено таким образом: на двух-трех столах дети раскладывают игрушки в равном количестве: на одном — по шесть, на другом — по восемь, на третьем — по десять (в выполнении этого задания может участвовать сразу несколько детей). Сопоставив число игрушек на своих столах, дети приходят к обобщению, что каждого вида игрушек на данном столе независимо от их характера по восемь. Число, обобщающее эти множества, конкретизируется: восемь петушков, восемь елочек, восемь курочек, восемь машин, восемь квадратов, восемь треугольников, восемь кубиков и т. д.; все игрушки разные, но всех их по восемь. Обобщение предметов по их количеству выступает в единстве с конкретизацией.

Таким образом, дети учатся абстрагировать число на основе взаимно-однозначного соответствия элементов равномощных множеств.

Это обобщение может и должно быть увязано с представлением о множестве. «А что мы можем сказать про все игрушки, стоящие на этом столе?» — спрашивает воспитательница. «На столе много разных игрушек».— «А кто догадается точнее сказать?» — «На столе много игрушек».— «Правильно. Что же можно еще сказать про данное множество?» — «Множество игрушек состоит из разных частей, разных видов игрушек. Там, где стоит по восемь игрушек в каждом ряду, всего семь частей,— считает ребенок ряды разных игрушек.— Все части равные, в каждой из них по восемь игрушек».

В данном ответе отражается понимание того, что единое множество может состоять из ряда частей и что все части могут быть выражены числом.

А это значит, что число для ребенка становится показателем мощности множества.

При варьировании подобных занятий задания могут быть разные. Например, детям, сидящим за одним столом, предлагается взять три вида игрушек по семь штук, а сидящим за Другим столом — по шесть и т. д. Здесь общий интерес поддерживается разными ответами детей каждой из групп. Но может быть и такой вариант, когда каждый ребенок получает индивидуальное задание. В этом случае у детей, сидящих за одним столом, задания разные. (Воспитательница заранее намечает, кому какое задание она даст.) При таком варианте занятия каждый ребенок должен запомнить указанное ему число и совершенно самостоятельно выполнить задание. Важно и на этих занятиях направлять внимание детей на связи между множеством и числом.

При другом варианте занятия на обобщение детям раздаются карточки с разным количеством нарисованных на них предметов, например восемь вишен, семь ягод малины, шесть огурцов, шесть помидоров и др. Наборы карточек у детей разные. Задача состоит в том, чтобы научить детей ориентироваться в этих количествах, запомнить и быстро поднимать карточки, на которых количество предметов соответствует количеству предметов, нарисованных на карточке воспитателя. Педагог показывает карточку с нарисованными геометрическими фигурами, например с шестью кругами, и предлагает детям поднять карточки с таким же количеством предметов. Если шесть предметов изображено на нескольких карточках, ребенок должен поднять все эти карточки (дети, не имеющие карточек с данным количеством, рук не поднимают). Поднятые карточки передаются соседу, который проверяет правильность ответа. Если у рядом сидящих детей имеется такое же количество, они тоже обмениваются своими карточками. Проверенные карточки откладываются в сторону нижней стороной вверх. Задание дается на другое число и проверяется так же. В конце воспитательница выясняет, у кого какие карточки остались незамеченными, чтобы дополнительно поупражнять этих детей. Об отложенных в сторону карточках, сгруппированных по признаку числа, дети рассказывают: «У нас три карточки, по шести предметов каждая: шесть помидоров, шесть огурчиков, шесть листьев березы и т. д.», «А у нас четыре карточки, по четыре предмета каждая: четыре желудя, четыре листа клена, четыре мяча, четыре вишни и т. д. Предметы разные, но их всех по четыре» (см. приложение 2).

Подобным способом описания дети овладевают постепенно: вначале они ограничиваются лишь названием игрушек и указанием их количества, обобщение же делает сама воспитательница или помогает делать его детям наводящими вопросами. Чтобы ответы детей не были шаблонными, вопросы нужно варь-

ировать, например: «Из каких частей состоит множество всех твоих карточек и сколько частей в твоем множестве? По скольку предметов на каждой карточке? Что можно сказать про все эти ряды множеств?» и др.

Итак, на занятиях данного вида дети наглядно знакомятся с равномощностью множеств, выраженных одинаковым числом; объединяют эти множества в одно общее, подсчитывают количество его частей. В процессе упражнений углубляется понимание детьми множества, а также значения числа как показателя мощности определенного класса множеств.

Изучение

Количественного

Состава числа

Из единиц.

Следующая группа занятий связана с изучением новой программной задачи — количественного состава числа из единиц. Надо не только показать детям, что всякое множество состоит из отдельных элементов (конкретных предметов или групп), но и разъяснить им отношение числа к единице, т. е. подчеркнуть количество единиц в числе.

Состав множества из отдельных элементов особенно нагляден, когда каждый элемент отличается от другого каким-либо признаком (цветом, размером, предметным содержанием и др.).

На начальных этапах множество для счета предлагалось однородным по качественным признакам, например восемь красных флажков. Но дети уже сами составляли множество из разнородных предметов (мишка, лошадка, кубик, заяц — это множество игрушек). На последующих этапах (в средней группе) детей знакомили с множеством как целым, но состоящим из разных частей, а в старшей группе — с объединением отдельных частей з единое целое. Дети научились уже дифференцировать элементы множества, правильно считать их. Теперь надо особо подчеркнуть отношения между единицей и числом, пока зать, что, например, число пять состоит из одного, еще одного, еще одного, еще одного и еще одного. Сделать это надо на конк-ректных множествах, например: пять флажков разных цветов; пять треугольников разного размера; пять разных игрушек — петух, мишка, утка, собака, гусь. Сначала дети считают эти множества, но воспитательница обращает их внимание на количественный состав, предлагает назвать количество и цвет каждого флажка, или размер каждого треугольника, или количество каждого вида игрушек. Пересчитав пять флажков, ребенок указывает, как составлено это пять, подчеркивая количественный состав: один — красный, один — синий, один — зеленый, один — желтый, один — голубой, а всего пять.

В дальнейшем дети сами составляют множества из разных предметов, определяют их состав. Следует обратить внимание на то, чтобы дети называли не только предметы, но и количество их: «Я взяла четыре игрушки: одного лебедя, одну черепаху, одну тарелку, одну рыбку».

На одном из занятий можно предложить детям по названному числу нарисовать множество из разных предметов. Однако, увлекаясь самим рисованием, дети часто забывают о количественных отношениях предметов, которые они должны отразить в своем рисунке, забывают то число, в соответствии с которым они должны нарисовать элементы множества. Поэтому включать счет в изобразительную деятельность надо лишь тогда, когда в основном дети овладели счетом. В противном случае преждевременное соединение двух сложных комплексных раздражителей может вызвать торможение неокрепших счетных связей.

Наблюдения за детьми и анализ их ошибок при изучении количественного состава числа из единиц показывают, как дети по-новому подходят теперь к тому же множеству. «Как получилось у тебя четыре?» — спрашивает воспитательница. Абстрагируясь от всех качеств предметов, ребенок отвечает: «Один, еще один, еще один и еще один». И хотя он еще опирается на предметы, находящиеся перед его глазами, сейчас его интересует лишь количественная сторона. Выделенные им элементы множества как бы абстрагируются в единицы, которые, суммируясь, составляют число четыре. «Сколько же ты взял разных игрушек, чтобы составить число четыре?» — спрашивает воспитательница, чтобы вернуть ребенка от абстракции числа к конкретному множеству и этим более прочно закрепить связи. «Я взял четыре разные игрушки: одного петуха, одного гуся, одну курицу, одну утку».

Важно, изучая количественный состав числа из единиц, подчеркнуть еще раз, что единица не есть отдельный предмет, а может быть отражением и целой группы. Воспитательница показывает детям множество кружков разного цвета, предлагая им определить количество частей в нем. Дети говорят, что данное множество составлено из пяти частей. «Назовите цвет и количество частей данного множества».— «В данном множестве пять частей разного цвета: одна часть — это красные кружки, одна — синие, одна — желтые, одна — зеленые и одна оранжевые кружки. А всего пять частей».— «Из скольких единиц состоит число пять?» — «Из пяти отдельных единиц».— «Что же может отражать единица?» — «Она может отражать один отдельный предмет или одну группу предметов»,— отвечают дети.

В итоге нескольких занятий дети усваивают количественный состав числа из единиц; уясняют, что число отражает соответствующее количество единиц, убеждаются, что число является показателем мощности множества. «Составьте мне множество из четырех частей»,— предлагает воспитательница. «Одна часть — ромашки, одна часть — васильки, одна часть — лютики и одна часть — гвоздики; а всего четыре части»,— говорят дети.

Механизм формирования этих отношений состоит из образования ряда ассоциаций. «Когда образуется связь,— говорит И. П. Павлов,— т. е. то, что называется «ассоциацией», это и есть, несомненно, знание дела, знание определенных отношений внешнего мира, а когда вы в следующий раз пользуетесь ими, то это называется «пониманием», т. е. пользование знаниями, приобретенными связями — есть понимание» '.

Строго дозируемая, последовательная система занятий создает условия для постепенного образования все новых и новых связей, формирующих знания детей. Развитие этих знаний идет от образования элементарного представления о множествах и понимания их взаимосвязей к пониманию числа как показателя мощности множества.